Square root and Approximations

Solving linear inequalities

Solving linear inequalities is similar to solving linear equations. All the rules and facts are same as for linear equation , only exception is that whenever we multiply or divide any inequality with a negative number, its sign get reversed. That means < sign get changed to > and viceversa.

Here are few examples to understand the process.

Example1. Solve the following inequality.

2(x-3) > 10

Solution: $\dpi{120} \frac{2(x-3)}{2}> \frac{10}{2}$

(x-3) > 5

X > 5+3

X > 8

Now we work on same example but with a negative sign and see how it effect the solution.

Example2. Solve the following inequality.

-2(x-3) > 10

Solution: To get rid of -2 , we divide both sides by -2 and therefore inequality sign get reversed.

$\dpi{120} \frac{-2(x-3)}{-2}< \frac{10}{-2}$

(x-3) < -5

X < -5+3 => x < -2

Representing the solution of an inequality : Solution of an inequality can be represented in two ways. One as an inequality and other as interval notation. To represent the solution in interval notation we need to be familiar with some rules.

Rules to convert the inequality in interval notation:

1) In interval notation smaller number is always written towards left (first place) and larger number is written towards right(second place). This rule would be helpful in solving double inequalities.

2) Solution having only < or > sign is represented with open brackets ( ) which means end points are not included

3) The solution having or is represented with closed brackets [ ] which means end points are included.

4) We always use parenthesis ( ) with infinity.

Here is a beautiful tabular representation of all these rules.

Representing the solution of inequality on a number line :

Inequality	Interval Notation	Number line representation
a<x<b	(a,b)
a≤x≤b	[a,b)
a<x≤ b	(a,b]
a≤x ≤b	[a,b]
X<b	(-∞ ,b)
x>a	(a, $\bg_white \large \mathbf{\infty}$ )
x ≤ b	(- $\dpi{120} \infty$ , b]
x ≥ a	[a, $\dpi{120} \infty$ )

Example3. Solve the following inequality and represent the solution as interval notation.

12-(2t+1) $\dpi{100} \geq$ 2(t-5)

Solution: First we remove parenthesis , for that we distribute – sign on left and 2 on right side of the inequality.

12 -2t-1 $\dpi{120} \geq$ 2t-10

-2t -2t $\dpi{120} \geq$ -10-12+1 (combining and rearranging like terms)

-4t $\dpi{120} \geq$ -21

$\dpi{120} \frac{-4t}{-4}\leq \frac{-21}{-4}$ (inequality reversed when divided by negative number)

$\dpi{120} t \leq \frac{-21}{4}$

In interval notation answer can be written as,

$\dpi{100} \left ( -\infty ,\frac{-21}{4} \right )$

Example4. Solve the following inequality and write the answer in interval notation. Also represent it on number line.

$\dpi{100} 7+\frac{1}{5}\left ( x-10 \right )\geq \left ( x+1 \right )$

Solution: Distributing 1/5 we get,

$\dpi{100} 7+\frac{x}{5}-2\geq \ x+1$

$\dpi{100} \frac{x}{5}-x\geq 1-7+2$

$\dpi{100} \frac{-4x}{5}\geq -4$

Multiply both sides with -5/4 to get x by itself,

$\dpi{100} \frac{-5}{4}*\frac{-4x}{5}\leq -4*\frac{-5}{4}$ (inequality reversed when multiplied by negative number)

x $\dpi{120} \leq$ 5

Interval notation: (- $\dpi{120} \infty$ , 5]

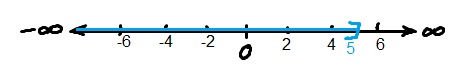
How to solve Double inequality: Solving double inequality is similar to solving single inequality but here we don’t move the variable to one side and numbers to other side as we do in solving single inequality. Our target is to get x all by itself and to get that,we use same operation to both sides. That means if we add or subtract something to middle x term, we do the same operation to left and right side terms too.

Example5. Solve the following inequality and represent the solution in interval notation.

7 < 5+2x < 1

Solution: 7 < 5+2x < 1

-5 -5 -5 (subtracting 5 from all sides)

2 < 2x < -4

$\dpi{120} \frac{2}{2}< \frac{2x}{2}< \frac{-4}{2}$

1 < x < -2

As per rules of writing interval notations, smaller number should be written first, so this inequality can be rewritten as,

-2 < x < 1

Which can be further written in interval notation as (-2,1)

Example6. Solve the given compound inequality and represent the solution in interval notation. Also represent the solution on number line. -10 < -5(x+2) $\dpi{120} \leq$ 6

Solution: -10 < -5x-10 $\dpi{120} \leq$ 6 (distributed -5) $\dpi{100} 7+\frac{1}{5}\left ( x-10 \right )\geq \left ( x+1 \right ){\color{Red} }$