Square root and Approximations

Scientific and Standard Notations

Scientific and standard Notations

When we think about writing very large or very small numbers in an easy and quicker way, scientific notation comes to our rescue.

Therefore, scientific notation is a way to represent very small or very large numbers. It is also easy to compare many such numbers when written in scientific notations

How scientific notation is written:

Scientific notation has two parts, first one is the coefficient and second part consists of base 10 and its exponent.

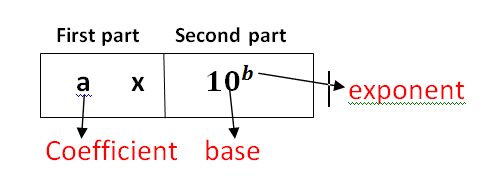
Coefficient is always a number between 1 and 10 . It may contain one or more than one significant digits with a decimal.

Base is always 10

Exponents is always an integer.

Converting from standard notation to scientific notation

When we move towards left, exponent is positive.

When we move towards right, exponent is negative.

Example1. Convert 450000 to scientific notation.

Solution: Since the coefficient must lie between 1 and 10 so decimal should be placed after 4. As decimal is moved 5 steps towards left we use positive exponent (5)

So the scientific notation is written as

$\dpi{120} 4.5\times 10^{5}$

Example2. Convert 0.000000215 to scientific notation.

Solution: This is very small number less than 1 so exponent would be negative.

Since coefficient must lie between 1 and 10 so we put decimal after first significant digit which is 2. For that we need to move decimal to 7 places right and whenever we move towards right while converting standard to scientific notation, we use negative exponents.

So the scientific notation is written as,

$\dpi{120} 2.15\times 10^{-7}$

Example3. Express 0.8 in scientific notation.

Solution: Since decimal should be placed after first significant digit so decimal is moved to right by only one place.

= $\dpi{120} 8.0\times 10^{-1}$

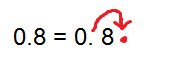
Or it can also be written as $\dpi{120} 8\times 10^{-1}$

Example4. Expression 30 in scientific notation.

Solution: Coefficient is the first significant digit which is 3 here, so we need to move decimal towards left by one place.

= $\dpi{120} 3.0\times 10^{1}$

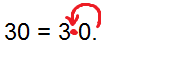
So 30 can be expressed in scientific notation as $\dpi{120} 3\times 10^{1}$

Converting from scientific notation to standard form

For given negative exponents we move towards left.

For given positive exponents we move towards right.

Example5. Convert $\dpi{120} {\color{Red} 4\times 10^{-5}}$ to standard notation.

Solution: Since decimal is not given here so we assume 4 as 4.0 and because of negative exponent(-5) we move 5 places towards left.

$\dpi{120} 4\times 10^{-5}$ =

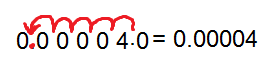
So the standard form of given number is 0.00004

Example6. Convert $\dpi{120} {\color{Red} 3.27\times 10^{4}}$ to standard form.

Solution: Since exponents is given positive so we move decimal towards right by 4 places.

$\dpi{120} 3.27\times 10^{4}$ =

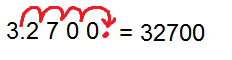
So the standard form of given number is 32700.

Example7. Express $\dpi{120} {\color{Red} 5.2\times 10^{0}}$ to standard form.

Solution: Since exponent is 0 that means we don’t need to move decimal. Moreover $\dpi{120} 10^{0} =1$ so the given number remain same without any change in it.