4. Linear equation in two variables

/by

All about linear equation in two variables.

In this video you will learn all about linear equations. Why they are called linear and why they have infinite solutions.

 

Graphing linear equations

Linear equations are graphed in 2D system (Cartesian system). In this video you will learn how to graph them. How to get solutions for linear equations when coefficient of x is a fraction. How to avoid getting points in fractions. Graphs of vertical and horizontal ines, how to find linear equations of word problems and also problems from ncert book.

3. Coordinate Geometry

/by

 

This chapter introduce you with coordinate planes and cartesian (2D) system. You will learn how a point is located in 2D system and the concept of quadrants.

 

How to find equations of x axis, y axis and the vertical and horizontal  lines.

 

2. Polynomials

/by

Factors, zeros, remainder, value of polynomial, all in one solution!

Behind most of the questions of exercise 2.2 and 2.3  there is only one concept. We can solve many type of problems by knowing only this concept and this chapter becomes so easy to understand. Here is the beautiful explanation in this video.

 

Super easy way to factor higher degree polynomials

Sometimes long division becomes difficult to use while factoring cubic polynomials or any higher degree polynomial. It is not easy to get first factor of cubic equation and then divide the equation by it to get next quadratic equation. So here is an extremely easy and quick way to divide the polynomial by a linear factor.

 

 

 

 

1. Number Systems

/by

How to find Rational number between two given numbers ?

This video explain two methods to find rational numbers between two given numvers. First method is good to use when you need to find only one rational number between them, but when you need to find two or more than two rational numbers then it would be better to use second method.

You will also learn how to find rational numbers between two simple numbers and between two fractions. Finding rational numbers between simple numbers is easy but we have to be careful while finding rational numbers between fractions.

 

Amazing trick to answer all T/F questions based on number system.

Sometimes it become hard to learn all the short questions based on number system. So here is the trick which you can use to answer all such T/F  questions. All you need to learn is, only a diagram and you are all set. So here is the trick explained in this video.

How to convert repeating decimal numbers to p/q form?

The following video explain how to convert repeating decimal numbers to p/q form. These repeating decimal numbers, which have bars over them, can be divided into two categories. There are only 2 steps (equations) in first category and 3 steps (equations) in second category. Keeping these two categoires in mind, would make this concept unforgettable to you.

Learn to draw any sqrt number on a number line.

In this video you will learn how to use the concept of Pythagoras to draw any sqrt number on a number line. First we break the given number using Pythagoras and then analyse that, which part to be used as base and which part to be used as perpendicular. After watching this video, you would be able to draw any sqrt number on your own.

 

Absolute and Conditional convergence

/by

How to check absolute convergence

Absolute convergence: If the absolute value 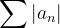\dpi{120} \sum \left | a_{n} \right |   of the series  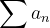, \dpi{120} \sum a_{n}  is convergent , then series  is called absolutely convergent.

Absolute convergence is a  stronger type of convergence.  Series that are absolutely convergent, are guaranteed to be convergent.  However, series that are convergent may or may not be absolutely convergent.

Lets look into some examples.

 

Example1: Does the following series converge absolutely.

\dpi{120} {\color{Red} \sum_{n=1}^{\infty }\frac{(-1)^{n+1}}{n^{3}}}

Solution: lets check the absolute value of this series first.

\dpi{120} \sum_{n=1}^{\infty }\left | a_{n} \right |=\sum_{n=1}^{\infty }\left |\frac{(-1)^{n+1}}{n^{3}} \right |= \sum_{n=1}^{\infty }\frac{1}{n^{3}}

Which is a P series .

Here p=3  which is greater than 1

The series is  convergent using P series test. So the given series converges absolutely

 

Example2: Check the following series for absolute convergence.

\dpi{120} {\color{Red} \sum_{n=1}^{\infty }\frac{sin(n)}{n^{2}}}

Solution:  First note that this is not alternating series but we can check its absolute convergence.

We know that sin ranges from -1 to 1

-1 ≤  Sin(n) ≤ 1

Which can be written as,  |sin(n)| ≤  1

Therefore,      \dpi{120} \left | \frac{sin(n)}{n^{2}} \right |\leq \frac{1}{n^{2}}

We know that 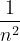 \dpi{120} \frac{1}{n^{2}}   is convergent by P series test as p=2 >1 .

By comparison test  given series is convergent.

Therefore the given series is absolutely convergent.

 

Conditional convergence:

When given series 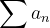\dpi{120} \sum a_{n} is  convergent but  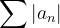\dpi{120} \sum \left |a_{n} \right |  is divergent then  we say series is conditionally convergent.

Let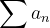\dpi{120} \sum a_{n} is a convergent series. We say that this series is Absolutely Convergent if 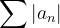\dpi{120} \sum \left |a_{n} \right |  is also convergent. We say the original series is Conditionally Convergent  if  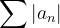\dpi{120} \sum \left |a_{n} \right |  is not convergent.

 

Example3: Check whether the following series is absolutely convergent ,  conditionally convergent or divergent.

\dpi{120} {\color{Red} \sum_{n=1}^{\infty }\frac{(-1)^{n}}{n}}
Solution:  This is an alternating harmonic series  and we use AST test to check its convergence, which is covered in previous section. Using AST we check its two conditions.

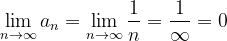
  1. \dpi{120} \lim_{n \to \infty }a_{n}=\lim_{n \to \infty }\frac{1}{n}= \frac{1}{\infty }=0
  2. This is a decreasing series because terms get decreased when denominators  get increased, which can be checked using derivative test too.

\dpi{120} (a_{n})'=\left (\frac{1}{n} \right )' = \frac{-1}{n^{2}}    which is always negative , that means this function(series) is  always decreasing.

Since both conditions  are met so this series is convergent  by AST.

Now we check its absolute convergence.

\dpi{120} \sum_{n=1}^{\infty }\left | a_{n} \right |=\sum_{n=1}^{\infty }\left |\frac{(-1)^{n}}{n} \right |= \sum_{n=1}^{\infty }\frac{1}{n}

Which is divergent being a harmonic series.

Here we saw that original series  is convergent by AST  but  it is not convergent absolutely  so this series is conditionally convergent.

 

 

Example4: Check whether the following series is absolutely convergent ,  conditionally convergent or divergent.

\dpi{120} {\color{Red} \sum_{n=1}^{\infty }(-1)^{n}\left ( n+\frac{1}{n} \right )}
Solution:  First we check  its convergence using AST . Lets check the two conditions:

1)   \dpi{120} \lim_{n \to \infty }a_{n}=\lim_{n \to \infty }\left (n+\frac{1}{n} \right )= \infty +0 =\infty

First condition is not satisfied , no need to check it further.

This series  is divergent by AST

We can also check it  is not absolutely convergent  using Limit comparison test.

So given series is divergent.

 

 

 

 

 

 

 

Practice problems:

In the following exercises determine whether the series is absolutely convergent, conditionally convergent, or divergent.

  1. \dpi{120} \sum_{n=1}^{\infty }\frac{(-1)^{n}}{2n}
  2. \dpi{120} \sum_{n=1}^{\infty }(-1)^{n}\frac{n^{2}+1}{n^{2}}
  3. \dpi{120} \sum_{n=1}^{\infty }\frac{(-1)^{n}}{2^{n}}      [ geometric series ]

 

 

 

 

 

 

Answers:

  • Conditionally convergent
  • Divergent
  • Convergent