What is Continuity
The meaning of term continuous is same as we use in our daily life. When we say that a function f(x) is continuous at point x=a, it means that at point (a,f(a)) graph of function has no holes or gaps. The graph is unbroken at point (a,f(a)).
A function is said to be continuous at a point x=a iff
- f(a) is defined
})
exist-
=&space;f(a)})
Any function f(x) fails to be continuous at x=a if it fail in any of three conditions given above and then it is called discontinuous function.
A function is continuous on interval [a,b] if it is continuous at each point of this interval.
Lets understand this concept of continuity and discontinuity with the help of graphs.
A function f(x) is said to be left continuous (continuous from left) at x=a, iff
)
exist and =&space;f(a))
A function f(x) is said to be right continuous(continuous from right) at x=a, iff
)
exist and =&space;f(a))
It follows from the above definition that f(x) is continuous at x=a iff it is both left and right continuous at x=a.
=\lim_{x\rightarrow&space;a^{+}}f(x)=&space;f(a)})
Algebra of continuous functions:
Let f and g be two real functions, continuous at x=a, then sum (f+g), difference (f-g) , product (f*g) and quotient (f/g) of these continuous functions will also be continuous at x=a.
In the next example lets learn how a graph can be discontinuous at different points and what it mean for a function to be continuous.
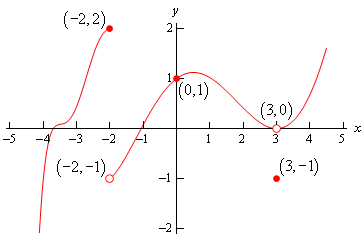
Example1 : Given the graph of f(x) shown below, check if f(x) is continuous at x=-2, x=0 and x=3.
Solution: At x= -2
We see that graph is left continuous at x=-2, That is
=2)
and f(-2)=2
But it is not right continuous , because
=&space;-1)
and f(-2)=2
Since limit doesn’t exist at x=-2 so this is discontinuous at x=-2 and this type of discontinuity is called jump discontinuity.
At x= 0,
Clearly graph is connected and smooth at x=0 . We can also see that both left and right sided limits are same as function value at x=0
=&space;f(0)=&space;1)
So graph is continuous at x=0
At x= 3,
We can see that limit is approaching to same value from either (left or right) sides. That is
=\lim_{x\rightarrow&space;3^{+}}f(x)=&space;0)
But f(3) = -1
That means &space;\neq&space;f(3))
So functions is discontinuous at x=3. This is called removable discontinuity.
Example2 : Test the continuity of given function at origin
=&space;\left\{\begin{matrix}&space;\frac{|x|}{x}&space;&&space;x\neq&space;0\\&space;1&space;&&space;x=0&space;\end{matrix}\right.})
Solution: Using the definition of absolute function we have,
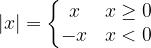
Using this definition we get the new transformed function as,
=\left\{\begin{matrix}&space;\frac{x}{x}&space;&&space;x>&space;0&space;\\&space;\frac{-x}{x}&space;&&space;x<&space;0&space;\\&space;1&&space;x=0&space;\end{matrix}\right.)
=\left\{\begin{matrix}&space;1&space;&&space;x>&space;0&space;\\&space;-1&space;&&space;x<&space;0&space;\\&space;1&&space;x=0&space;\end{matrix}\right.)
We have f(x) =1 for domain x >0 that means right sided limit at x=0 is 1
=\lim_{x\rightarrow&space;0}1=1)
We have f(x) =-1 for domain x <0 that means left sided limit at x=0 is -1
=\lim_{x\rightarrow&space;0}(-1)=-1)
Since left and right sided limits are not same,
\neq&space;\lim_{x\rightarrow&space;0^{-}}f(x))
So limit doesn’t exist at x=0 and therefore function is not continuous at x=0.
Example3: Consider the function
=\left\{\begin{matrix}&space;x^{2}-3x&space;&x<&space;-1&space;\\&space;2x-3&space;&&space;-1\leq&space;x<&space;1\\&space;2&space;&&space;x=1\\&space;\frac{1}{x-2}&space;&&space;x\geq&space;1&space;\end{matrix}\right.})
Evaluate the following expressions. When a limit fails to exist, cite the reason why this is the case. Then identify all discontinuities present.
- f(-1)
- f(1)
})
})
})
})
Solution 1):
Since x = -1 lie in the domain -1 ≤ x < 0 so we consider function f(x)= 2x-3 to find f(-1)
f(-1) = 2(-1)-3 = -5
2)
Given f(1)= 2
3)
We need to check left and right sided limit at x=-1. For that we choose respective domains.
left sided limit:
=\lim_{x\rightarrow&space;-1}x^{2}-3x&space;=&space;(-1)^{2}-3(-1)=4)
Right sided limit:
=\lim_{x\rightarrow&space;-1}2x-3&space;=2(-1)-3&space;=-5)
Since left and right sided limits are not same so limit doesn’t exist at x=-1.
4)
x=0 lie in the domain -1 x < 1 and function given for this domain is f(x)=2x-3
=\lim_{x\rightarrow&space;0}2x-3&space;=2(0)-3&space;=-3)
5)
For this too we find left and right sided limits at x=1
Left sided limit:
=\lim_{x\rightarrow&space;1}2x-3&space;=&space;2(1)-3=-1)
Right sided limit:
=\lim_{x\rightarrow&space;1}\frac{1}{x-2}&space;=&space;\frac{1}{1-2}&space;=-1)
Left and right sided limits are same so limit exist
=-1)
6) =&space;\lim_{x\rightarrow&space;2}\frac{1}{x-2})
We see that x=2 is a vertical asymptote here. Lets check left and right sided limits at x=2
Lets assume a very small quantity ‘h’ which tends to 0 and can be used judiciously for left and right sided limits.
Left sided limit:
=\lim_{h\rightarrow&space;0}f(2-h)=&space;\lim_{h\rightarrow&space;0}\frac{1}{2-h-2}&space;=&space;\frac{-1}{h}=&space;-\infty)
Right sided limit:
=\lim_{h\rightarrow&space;0}f(2+h)=&space;\lim_{h\rightarrow&space;0}\frac{1}{2+h-2}&space;=&space;\frac{1}{h}=&space;\infty)
Since left and right limits are not same at x=2 so limit doesn’t exist at x=2
Lets discuss discontinuities now. Clearly function is not continuous where limit doesn’t exist. So this function is not continuous at x=-1 and x=2.
Limit exist at x=0 and linear functions are always continuous in their domains. So this function is continuous at x=0.
We see that limit exist at x=1 but it is not same as the function value at x=1
=\lim_{x\rightarrow&space;1^{+}}f(x)=-1)
But f(1)= 2
Which shows there is a hole and so the function is not continuous here.
Example4 : If =\left\{\begin{matrix}&space;1&space;&&space;x\leq&space;3&space;\\&space;ax+b&&space;3<&space;x<&space;5&space;\\&space;7&&space;5\leq&space;x&space;\end{matrix}\right.})
Determine the values of a and b so that f(x) is continuous.
Solution: Given function is a constant function for all x<3 and for all x>5 so it is continuous for all x values in these domains. For domain 3<x<5 given function is linear function and linear function is always continuous in its domain. Therefore f(x) is continuous at each x∈R except possibly at x=3 and x=5.
At x=3,
Left limit:
=&space;\lim_{x\rightarrow&space;3}(1)&space;=&space;1)
and f(3) =1
Right Limit:
=&space;\lim_{x\rightarrow&space;3}(ax+b)&space;=&space;3a+b)
For f(x) to be continuous at x=3, we must have
=\lim_{x\rightarrow&space;3^{+}}f(x)=&space;f(3))
1 = 3a+b ——-(i)
At x=5,
Left limit:
=&space;\lim_{x\rightarrow&space;5}(ax+b)&space;=&space;5a+b)
Right limit:
=&space;\lim_{x\rightarrow&space;5}(7)&space;=&space;7)
and f(5) =7
For f(x) to be continuous at x=5, we must have
=\lim_{x\rightarrow&space;5^{+}}f(x)=&space;f(5))
5a+b=7 ——-(ii)
Solving equations (i) and (ii)
3a+b =1
5a+b=7
we get, a=3 and b=-8
Practice problems:
1) A function f(x) defined as =&space;\left\{\begin{matrix}&space;\frac{x^{2}-9}{x-3}&space;&&space;x\neq&space;3\\&space;6&space;&&space;x=3&space;\end{matrix}\right.)
Show that f(x) is continuous at x=3.
2) Consider the function
=\left\{\begin{matrix}&space;\frac{2x+3}{x+2}&space;&&space;x<&space;1&space;\\&space;x^{2}&space;&1\leq&space;x<&space;2&space;\\&space;5x-6&space;&&space;x\geq&space;2&space;\end{matrix}\right.)
Evaluate the following expressions. When a limit fails to exist, cite the reason why this is the case. Then identify all discontinuities present.
3 ) Determine the value of constant k so that the function
is continuous at x=0.
Answers:
2) f(2)=4 , Limit doesn’t exist at x=-2,1 ; =4)
3) 2/5
