Subtopic Archive - Page 9 of 10

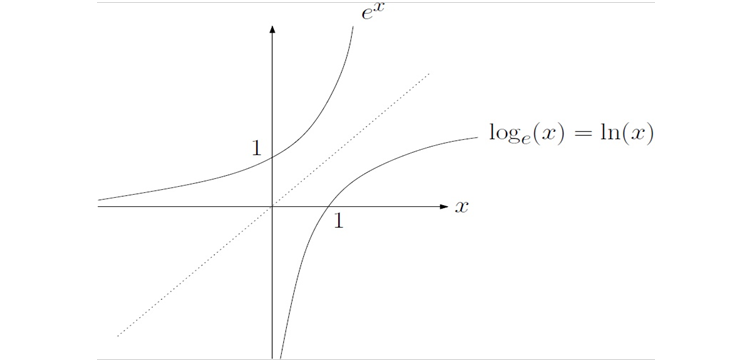
Transforming and Graphing logarithmic functions

August 13, 2019/by admin_ct

Graphing logarithmic functions

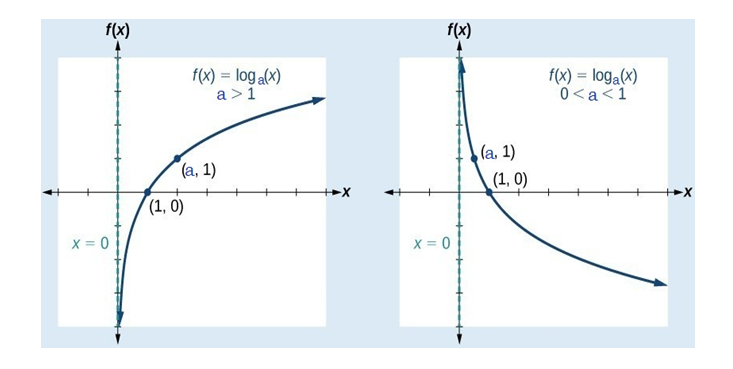
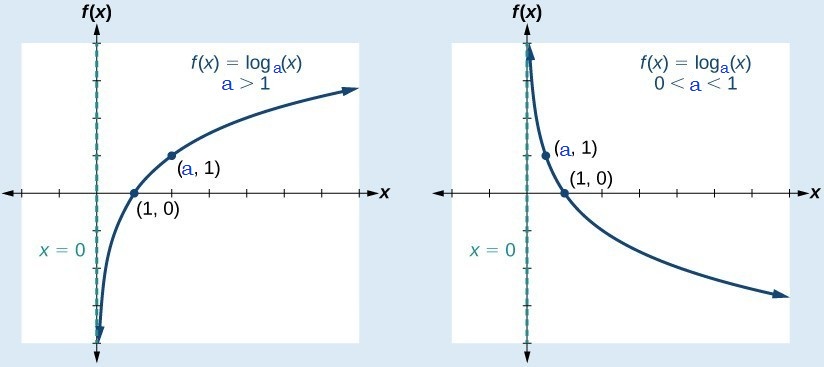
There are two possible cases of logarithmic function $\dpi{120} \mathbf{\log_{a}x}$ .

Case 1. When a>1

Then logarithmic function is increasing function with x intercept as (1,0).

Case 2. When 0<a<1

Then logarithmic function is decreasing function with x intercept same as (1,0).

Following graph will help you to observe the similarity and difference between two cases.

$C:\Users\Suman Gupta\Documents\graph logs.jpg$

Transformation of log functions

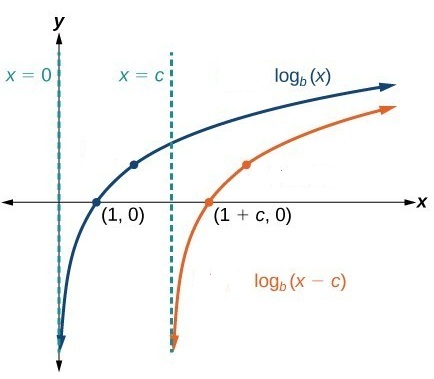
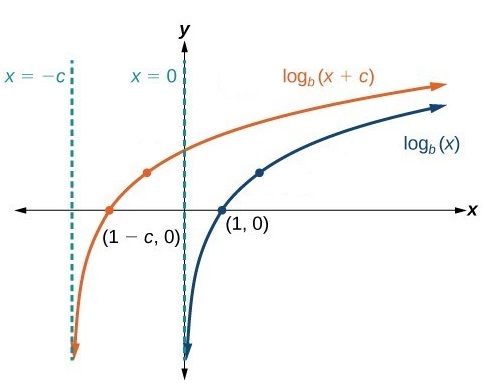
To graph log functions we need to understand the different transformations with respect to the parent log function $\dpi{120} \mathbf{\log_{b}x}$ .
Here is a beautiful summary of all the transformations and the effect of these transformations on different parameters like domain, x-intercept, vertical asymptotes etc.

Function f(x)	Transformation	V.A.	X -Intercept	Domain	Range
$\dpi{120} \log_{b}x$	None	X=0	(1,0)	(0, ∞)	(-∞,∞ )
$\dpi{120} \log_{b}\left (x-c \right )$	Shift right	X=c	(1+c,0)	(c, ∞)	(-∞,∞)
$\dpi{120} \log_{b}\left (x+c \right )$	Shift left	X=-c	(1-c,0)	(-c,∞ )	(-∞,∞)
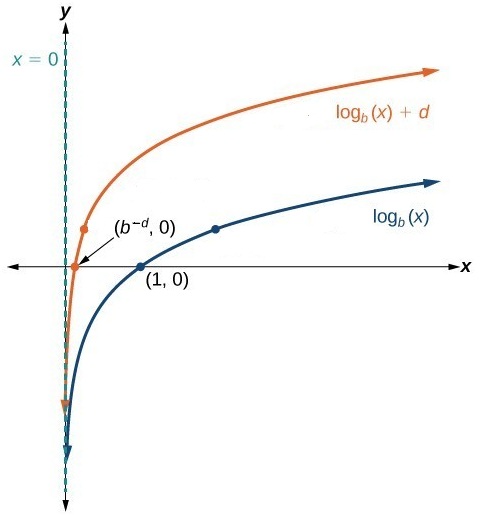
$\dpi{120} \log_{b}x+d$	Shift up	X=0	( $\dpi{120} b^{-d}$ ,0)	(0,∞ )	(-∞,∞)
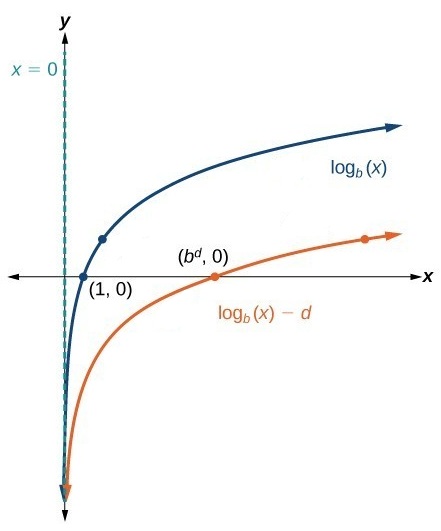
$\dpi{120} \log_{b}x-d$	Shift down	X=0	( $\dpi{120} b^{d}$ ,0)	(0, ∞)	(-∞,∞)
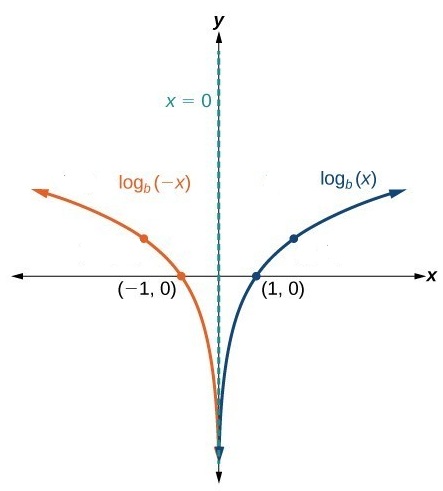
$\dpi{120} \log_{b}(-x)$	Reflection across y axis	X=0	(-1,0)	(-∞,0 )	(-∞,∞)
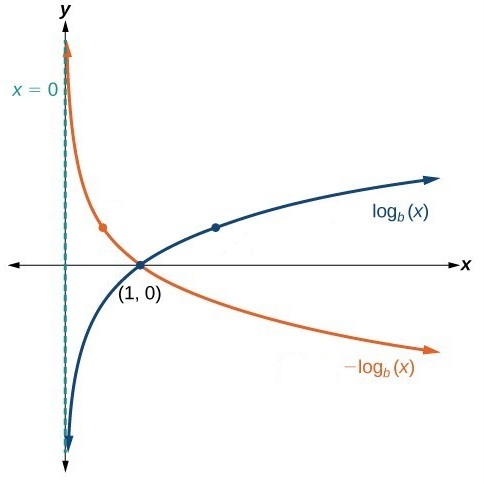
– $\dpi{120} \log_{b}x$	Reflection across x axis	X=0	(1,0)	(0,∞ )	(-∞,∞)
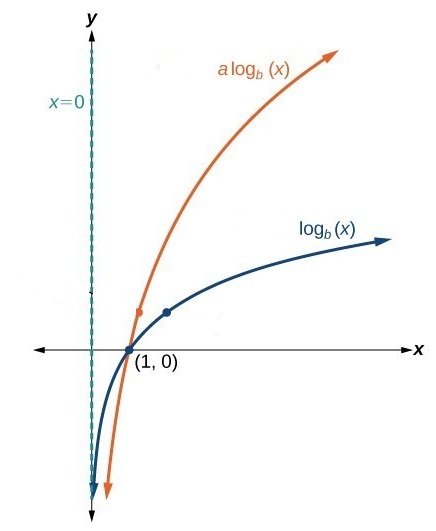
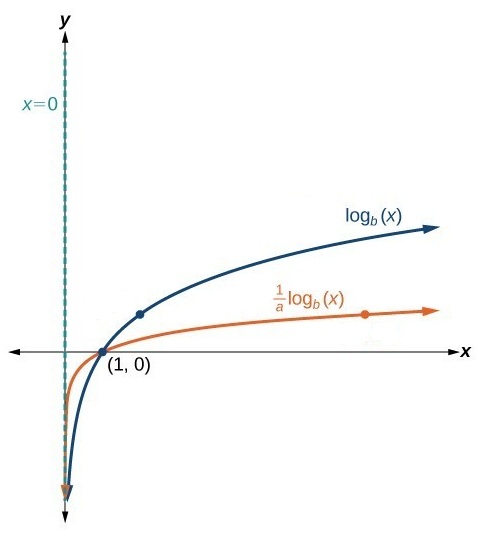
$\dpi{120} a\log_{b}x$	Vertical stretch	X=0	(1,0)	(0,∞ )	(-∞,∞)
$\dpi{120} \frac{1}{a}\log_{b}x$	Vertical compression	X=0	(1,0)	(0, ∞)	(-∞,∞)
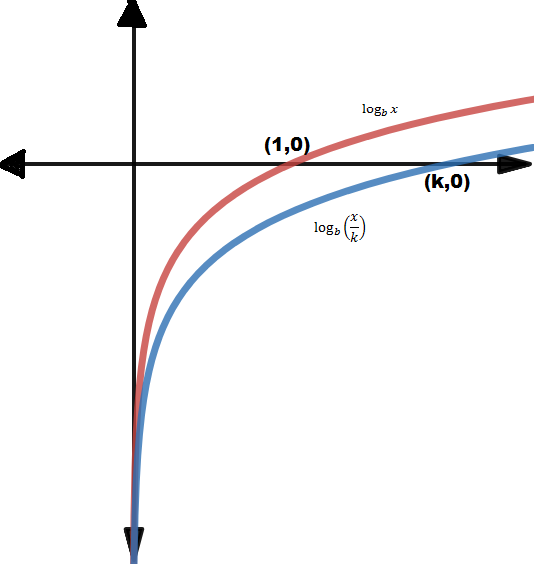
$\dpi{120} \log_{b}\left (x/k \right )$	Horizontal stretch	X=0	(k,0)	(0, ∞)	(-∞,∞)
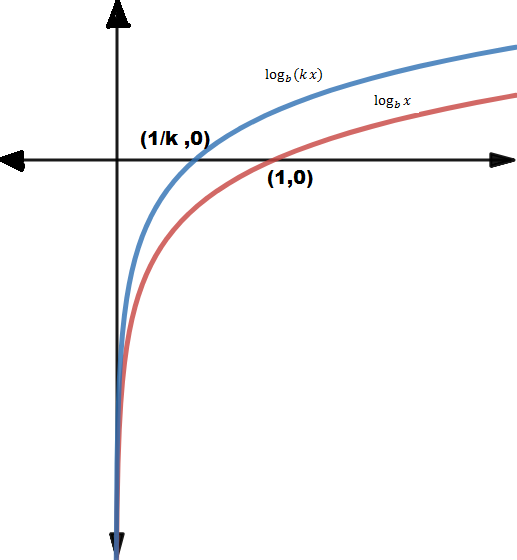
$\dpi{120} \log_{b}\left (kx \right )$	Horizontal compression	X=0	( 1/k ,0)	(0,∞)	(-∞,∞)

And their respective graphs are shown below:

$\mathbf{log_{b} (x -c)}$	$C:\Users\Suman Gupta\Documents\log 1-2.jpg$
$\mathbf{log_{b} (x +c)}$	$C:\Users\Suman Gupta\Documents\log 1-1.jpg$
$\mathbf{log_{b} (x)+ d}$	$C:\Users\Suman Gupta\Documents\log2-1.jpg$
$\mathbf{log_{b} (x)- d}$	$C:\Users\Suman Gupta\Documents\log2-2.jpg$
$\mathbf{log_{b} (-x)}$	$C:\Users\Suman Gupta\Documents\log3-2.jpg$
$\mathbf{-log_{b} (x)}$	$C:\Users\Suman Gupta\Documents\log3-1.jpg$

$\mathbf{{a}log_{b}(x)}$	$C:\Users\Suman Gupta\Documents\log4-1.jpg$
$\mathbf{\frac{1}{a}log_{b}(x)}$	$C:\Users\Suman Gupta\Documents\log4-2.jpg$
$\mathbf{log_{b} \left (\frac{x}{k} \right )}$	$C:\Users\Suman Gupta\Documents\log7.png$
$\mathbf{log_{b} \left ( kx \right )}$	$C:\Users\Suman Gupta\Desktop\graph 8.png$

Lets work on an example of combined transformation.

Example1 : Sketch the graph of y=log(x-2)+3 and state its domain, range , x intercept and vertical asymptote.

Solution: For this graph two steps of transformations are used with respect to parent function graph.

Parent function y= log(x)

Step1. Shift the basic graph to right by 2 units

Y= log(x-2)

Step 2) then shift the graph up by 3 units

Y= log(x-2) + 3

And we get the graph as shown by blue graph below.

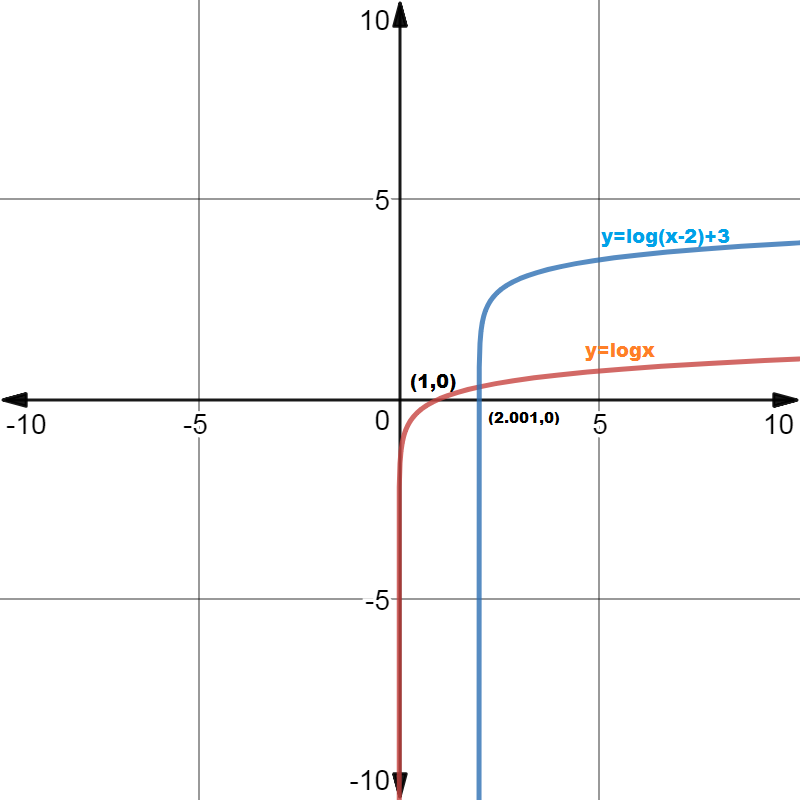
$C:\Users\Suman Gupta\Downloads\graph 1.png$

Domain: (2, $\infty$ )

Range: (- $\infty$ , $\infty$ )

Vertical asymptote : x=2

X intercept : = $\mathbf{\left ( b^{-d}+c,0 \right )=\left ( 10^{-3} +2,0 \right ) = \left ( 2.001,0 \right ) }$

Example2: Sketch the graph of y=2log(3-x)-1 and state its domain, range , x intercept and vertical asymptote. Analyze it for increasing and decreasing behavior, continuity , symmetry and end behavior.

Solution: Rewriting given function in standard form we get,

Y=2log(-(x-3))-1

Now we apply following procedure to get its graph from parent function y= logx

Step 1) Shift the graph to right by 3 units.

Y = log(x-3)

Step 2) Reflect the graph along y axis.

Y= log(-(x-3))

Step3) Stretch the graph vertically by 2 units.

Y = 2log(-(x-3))

Step 4) Shift the graph down by 1 unit.

Y = 2log(-(x-3))-1

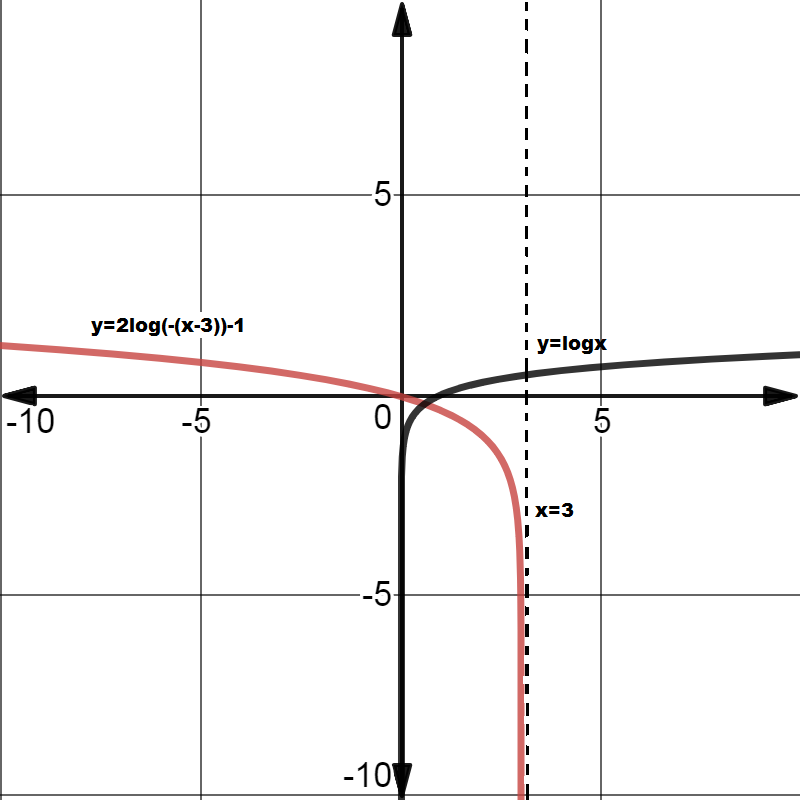
$C:\Users\Suman Gupta\Documents\logs 1.png$

Decreasing everywhere.

Continuous in its domain (- $\infty$ ,3)

Not symmetric

End behavior: = $\mathbf{\lim_{x\rightarrow -\infty }f\left ( x \right )=\infty } , \lim_{x\rightarrow 3^{-}}f(x)=-\infty$

Practice problems:

Sketch the graph of following log functions and state their domain, range, asymptotes and intercepts if any.

Y= ln(x) +2
Y=log(x-3)
Y=-3log(-x)
Y=-3log(1-x)+1

Domain and Range of log function

August 12, 2019/by admin_ct

Domain of different log functions:

The domain of the function of the form $\dpi{120} \mathbf{f(x)= \log_{x}A}$ is given as x>0 where x≠ 1. It should be noted that x appears as base here. Writing this domain in interval form , we get

Domain : (0,1)U(1,∞ )

Whereas the domain of the function of the form $\dpi{120} \mathbf{f(x)= \log_{b}x}$ is all the non negative real numbers.

Domain: (0, ∞ )

Note: Log functions are never defined for 0 and negative numbers and range of logarithmic function $\dpi{120} \mathbf{f(x)= \log_{b}x}$ is all real numbers.

Lets work on some examples where argument (input to the log) of log function may be some rational function , radical function or some other form.

Example 1.Find domain of the given function.

$\dpi{120} {\color{Red} f(x)=\log_{10}\left ( \frac{x^{2}-7x+12}{x^{2}-4x+7} \right )}$

Solution: Here argument of log function is a rational function. As we know that log is never defined for 0 and negative values so we have to see where this rational function have positive values.

$\dpi{120} \frac{x^{2}-7x+12}{x^{2}-4x+7}> 0$

Here function in the denominator doesn’t have real roots and positive leading coefficient ensures that this will always give positive output for all x values. That means we are only bothered by the expression on top as denominator is always a positive value.

$\dpi{120} x^{2}-7x+12>0$

(x-4)(x-3) > 0

Intervals	(x-4)(x-3)	Result
(-∞, 3)	(-)(-)	+
(3,4)	(-)(+)	–
(4,∞ )	(+)(+)	+

So the domain of given log function is (-∞,3)U(4,∞ )

Using these values of x we get that maximum value of function occurs at x=0. So range of this function would be (-∞ , log(12/7 )] or (-∞ ,0.234]

Example 2. Find domain of the given log function.

$\dpi{120} {\color{Red} f(x)= \sqrt{\log_{10}\left ( \frac{6x-x^{2}}{8} \right )}}$

Solution: As radicals are not defined for negative values ,

Therefore , $\dpi{120} \log_{10}\left ( \frac{6x-x^{2}}{8} \right )\geq 0$

converting log equation into exponential equation we get,

$\dpi{120} \frac{6x-x^{2}}{8}\geq 10^{0}$

$\dpi{120} 6x-x^{2}\geq 8(1)$ $\dpi{120} \left [10^{0}=1 \right ]$

$\dpi{120} 0\geq 8-6x+x^{2}$

$\dpi{120} x^{2}-6x+8\leq 0$

(x-4)(x-2)≤ 0

Using x=2,4 we get the intervals as (-∞, 2), (2,4), (4,∞ )

Intervals	(x-4)(x-2)	Result
(-∞, 2)	(-)(-)	+
(2,4)	(-)(+)	–
(4,∞)	(+)(+)	+

So only interval(2,4)is accepted. Which is the domain of radical function. Next we find domain of log function.

$\dpi{120} \frac{6x-x^{2}}{8}\geq 0$

$\dpi{120} 6x-x^{2}\geq 0$

x(6-x) ≥ 0

Solving this we get two values x=0,6. Using these two values we get the intervals as. (-∞, 0), (0,6), (6, ∞) and get a sign chart as follows.

Intervals	x(x-6)	Result
(-∞, 0)	(-)(+)	–
(0,6)	(+)(+)	+
(6,∞ )	(+)(-)	–

Only interval(0,6) is accepted.

To find final domain of complete function we find intersection of both intervals (2,4) and (0,6).

Domain: (2,4) ∩(0,6) = [2,4]

Range: When we plug in x=2 and x=4 we get y=log1=0. Observing values between 2 and 4 we see that maximum value is obtained at x=3. At x=3 we get

$\dpi{120} y=\sqrt{\log_{10}\left (\frac{9}{8} \right )} =0.226$

Range : [0, 0.226]

Example3. Find domain and range of given function.

$\dpi{120} {\color{Red} f(x)= log\sqrt{9-x^{2}}}$

Solution: We know that log is never defined for 0 and negative values . That means $\dpi{120} \sqrt{9-x^{2}}> 0$

$\dpi{120} 9-x^{2}> 0$

(3-x)(3+x) > 0

-3, 3 > x

Using x=-3,3 we get intervals as (-∞ ,-3), (3,3) ,(3,∞ )

Intervals	(3-x)(3+x)	Result
(-∞, -3)	(+)(-)	–
(-3,3)	(+)(+)	+
(3,∞ )	(-)(+)	–

Therefore, domain of this function is

Domain: (-3,3)

To find range we plug in x values as in the domain (-3,3) and get maximum value at x=0. So its range is given as,

Range: (-∞ , log3]

Practice problems:

Find domain and range of given log functions:

$\dpi{120} f(x)= \log_{10}\left ( \sqrt{5-x}+\sqrt{x-1}\right )$
$\dpi{120} f(x)=\log_{10}\left ( x^{2}-3x+4 \right )$
$\dpi{120} f(x)=\log_{10}\left ( x^{2}-4 \right )$
$\dpi{120} f(x)=log\left ( x^{2}-5x+6 \right )$
$\dpi{120} f(x)=\log_{10}\left ( x+5 \right )$

Answers:

Domain: [1,5] , Range :[log2, log2√2 ]
Domain: (-∞,∞ ), Range:[log( 7/4) ,∞ )
Domain: (-∞ ,-2) U (2,∞ ) Range: (-∞,∞)
Domain: (-∞ ,2) U (3,∞ ) Range: (-∞,∞ )
Domain: (-5, ∞) Range : (-∞,∞)

Applications of exponential functions (Intensity of earthquakes and sound loudness)

August 12, 2019/by admin_ct

Intensity of earthquakes and sound loudness

Richter scale is a logarithmic function to measure strength of earthquakes and its formula is given as,

$\dpi{150} \mathbf{R=log \left ( \frac{I}{I_{0}} \right )}$

Here R is the Richter scale magnitude of earthquake and $\dpi{120} \frac{I}{I_{0}}$ is the intensity ratio of earthquakes.

The intensity of earthquake will typically measure between 2 and 10 on Richter scale.

Example1: An earthquake is measured with a wave intensity 200 times as great as I₀. What is the magnitude of this earthquake using the Richter scale, to the nearest tenth?

Solution: Given that wave intensity 200 times as great as I₀

So $\dpi{120} I= 200I_{0}$

Substituting these values into the formula, we get

R = log(200) = 2.3

Magnitude of this earthquake is 2.3 on Richter scale.

Above formula can also be used in another form when Richter magnitude of two earthquakes is given and we need to compare their intensities.

$\dpi{150} \mathbf{\frac{I}{I_{0}}= 10^{M-M_{0}}}$

Where $\dpi{120} M_{0}$ is the magnitude of weaker earthquake and M is the magnitude of stronger earthquake.

Example2: A small tremor of magnitude 3.4 is followed by strong one of magnitude 4.1. How much stronger is the second tremor than the first one.

Solution: Here we need to find intensity of earthquakes.

Using formula $\dpi{120} \frac{I}{I_{0}}= 10^{M-M_{0}}$

$\dpi{120} \frac{I}{I_{0}}= 10^{4.1-3.4}$

$\dpi{120} \frac{I}{I_{0}}= 5.01$

Second tremor is 5 times stronger than the first one.

Example3: A strong earthquake with a magnitude of 5.7 is three times more intense than the weaker earthquake. Find the magnitude of weaker earthquake

Solution: Given that M =5.7 and $\dpi{120} I=3I_{0}$ . We need to find $\dpi{120} M_{0}$ .

$\dpi{120} \frac{3I_{0}}{I_{0}}=10^{5.7-M_{0}}$

$\dpi{120} 3=10^{5.7-M_{0}}$

$\dpi{120} log3=log10^{5.7-M_{0}}$

$\dpi{120} log3=(5.7-M_{0})log10$

$\dpi{120} 0.477 = 5.7-M_{0}$

$\dpi{120} M_{0}=5.02$

Formula for loudness of sound using sound intensity is :

$\dpi{150} \mathbf{dB-dB_{0}= 10log\left ( \frac{I}{I_{0}} \right )}$

Where dB is decibel value of loud sound and $\dpi{120} dB_{0}$ is decibel value of soft sound. $\dpi{120} \left ( \frac{I}{I_{0}} \right )$ is the intensity ratio of sounds.

Example4: A sound of 75dB is 50 times louder than a weaker sound. What is the loudness of weaker sound.

Solution: $dB-dB_{0}= 10log\left ( \frac{I}{I_{0}} \right )$

$75-dB_{0}= 10log\left ( \frac{50I_{0}}{I_{0}} \right )$

$75-dB_{0}= 10log\left ( \50 \right )$

$75-dB_{0}= 16.989$

$dB_{0}= 75-16.99= 58.01$

Example5: Two different sounds has their loudness level as 80 dB and 100dB. How much louder is the second sound?

Solution: $dB-dB_{0}= 10log\left ( \frac{I}{I_{0}} \right )$

$100-80= 10log\left ( \frac{I}{I_{0}} \right )$

$\frac{20}{10}= log\left ( \frac{I}{I_{0}} \right )$

$2= log\left ( \frac{I}{I_{0}} \right )$

$10^{2}=\frac{I}{I_{0}}$

$100 I_{0}=I$

So the louder sound is 100 times intense than the weaker sound.

Formula to find acid strength is:

$\dpi{150} \mathbf{pH=-log[H^{+}]}$

Where is the concentration of hydrogen ion and pH is acid strength(power of hydrogen)

Example6: Calculate the pH of the acid which has concentration of $\dpi{120} {\color{Red} H^{+}}$ ions as $\dpi{120} {\color{Red} 2.5\times 10^{-5}}$ .

Solution: $pH=-log[H^{+}]$

$pH=-log[2.5\times 10^{-5}]$

pH = 4.60

Example7: Find hydrogen concentration of acid which has a pH value of 3.7

Solution: $pH=-log[H^{+}]$

$3.7=-log[H^{+}]$

$-3.7=log[H^{+}]$

$10^{-3.7}=[H^{+}]$

$\dpi{120} 1.99\times 10^{-4} mol/L=\left [ H^{+} \right ]$

Practice problems:

A small tremor of magnitude 2.3 is followed by strong one of magnitude 5.3. How much stronger is the second tremor than the first one.
A strong earthquake with a magnitude of 5.9 is one thousand times more intense than the weaker earthquake. Find the magnitude of weaker earthquake.
A sound of 70dB is 8900 times louder than a weaker sound. What is the loudness of weaker sound.
Two different sounds has their loudness level as 97 dB and 110dB. How much louder is the second sound?
Find hydrogen concentration of acid which has a pH value of 8.7

Answers:

1000
2.9
30.5 dB
20
$\dpi{120} 2\times 10^{-9}$ mol/L

Applications of exponential and logarithmic functions (Population and bacteria growth)

August 11, 2019/by admin_ct

Population and bacteria growth

Exponential growth and decay: For growth and decay word problems we use formula:

$\dpi{150} \mathbf{A=A_{0}\left ( b \right )^{\frac{t}{p}}}$

Where A=Amount after certain time

$A_{0}$ =Initial amount

b = Type of growth

t = time elapsed

p= period for growth to occur

Example1: A bacterial culture doubles every 3 hours. If the culture started with 20,000 bacteria, how many will be present in 4 hrs.

Solution: Given that culture doubles every 3 hrs.

That means b=2 and p= 3

Also given initial amount $A_{0}= 20,000$ and time t= 4

Using formula, $\dpi{120} A=A_{0}\left ( b \right )^{\frac{t}{p}}$

$A= 20,000\left ( 2\right )^{\frac{4}{3}}$

A = 50396.8419

A = 50397 bacteria

Example 2: Population of a town triples every 5 years. If 4000 people were present in year 2005, then find the population in year 2015.

Solution: Given that population triples every 5 years.

That means b=3 and p= 5

Also given initial population $A_{0}= 4,000$

Time elapsed (t)=2015-2005= 10 years.

Using all these values into same formula, we get

$A= 4,000\left ( 3\right )^{\frac{10}{5}}$

A = 4000(9) =36,000

Solving for variable other than A.

Example3: Population of a town changes by exponential growth factor b every 4 years. If 2350 grows to 7000 in 3 years, what is the value of b.

Solution: Given initial population $A_{0}= 2350$

Final population A =7000

Time elapsed (t)= 3 yrs

p= 4 yrs

using formula, $\dpi{120} A=A_{0}\left ( b \right )^{\frac{t}{p}}$

$7000= 2350\left ( b\right )^{\frac{3}{4}}$

$\frac{7000}{2350}= \left ( b\right )^{\frac{3}{4}}$

$\ln \left (\frac{7000}{2350} \right )= \ln \left ( b\right )^{\frac{3}{4}}$ (taking ln of both sides)

$\ln \left (\frac{7000}{2350} \right )= \frac{3}{4}\ln \left ( b\right )$ (using formula $\dpi{120} \ln x^{y}= y\ln x$ )

$\frac{4}{3}\ln \left (\frac{140}{47} \right )= \ln \left ( b\right )$
1.4553.. = ln(b)

$\dpi{120} e^{1.4553...}= b$

4.3 = b

Example4: A bacterial culture double every 5 hours. How long will it take for a culture to quadruple?

Solution: Given that culture doubles every 5hrs.

So b=2 and p= 5

Also given, $\dpi{120} A=4A_{0}$

Using formula we get, $\dpi{120} 4A_{0}=A_{0}\left ( 2 \right )^{\frac{t}{5}}$

$\dpi{120} 4= 2^{\frac{t}{5}}$

$\dpi{120} ln4= ln2^{\frac{t}{5}}$

$\dpi{120} ln4= \frac{t}{5}ln2$

$\dpi{120} \frac{ln4}{ln2}= \frac{t}{5}$

$\dpi{120} \frac{2ln2}{ln2}= \frac{t}{5}$

$\dpi{120} 2= \frac{t}{5}$

2(5) =t => t= 10 hours

Example5: A radioactive sample has half life of 3 days. How long will it take for only 1/8^th of the sample to remain?

Solution: Give that half life of 3 days.

That means b= ½ and p= 3

Also given that A = 1/8^th of initial sample, so $\dpi{120} A= \frac{1}{8}A_{0}$

$\dpi{120} \frac{1}{8}A_{0}= A_{0}\left ( \frac{1}{2} \right )^{\frac{t}{3}}$

$\dpi{120} \frac{1}{8}= \left (\frac{1}{2} \right )^{\frac{t}{3}}$

$\dpi{120} \left ( \frac{1}{2} \right )^{3}= \left ( \frac{1}{2} \right )^{\frac{t}{3}}$ (When bases are same, powers can be equated)

3 = t/3 => t= 9 days.

Example6: Light passing through murky water retain 3/4^th of its intensity for every meter of water. At what depth will the light intensity be 60% of what it is at the surface?

Solution: Final amount is always the remaining amount. Here remaining light intensity is 60% so we can use final amount A as $\dpi{120} 0.6A_{0}$

Given that water retain3/4^th of its intensity, so b=3/4 and p=1.

Using the values into the formula we get,

$\dpi{120} 0.6A_{0}=A_{0}\left ( \frac{3}{4} \right )^{\frac{t}{1}}$

$\dpi{120} 0.6 =(0.75)^{t}$

ln(0.6) = ln(0.75)^t

ln(0.6) = t ln(0.75)

$\dpi{120} \frac{ln(0.6)}{ln(0.75)}=t$

1.78 m = t

Example7: A radioactive sample has a half life of 3 years and has initial mass of 68 g. How long will it take for the sample to loose 8g ?

Solution: Here the final amount A, would be the remaining amount . So = 68-8= 60 g.

Note : Avoid using lost amount 8g as remaining final amount.

Given half life of 3 years, that means b=1/2 and p=3

$\dpi{120} A=A_{0}\left ( b \right )^{\frac{t}{p}}$

$\dpi{120} 60= 68\left ( \frac{1}{2} \right )^{\frac{t}{3}}$

$\dpi{120} \frac{60}{68}= \left ( \frac{1}{2} \right )^{\frac{t}{3}}$

$\dpi{120} ln\frac{15}{17}= ln\left ( \frac{1}{2} \right )^{\frac{t}{3}}$

$\dpi{120} ln\frac{15}{17}= \frac{t}{3}ln\left ( \frac{1}{2} \right )$

$\dpi{120} \frac{ln\frac{15}{17}}{ln\frac{1}{2}}=\frac{t}{3}$

$\dpi{120} 3\frac{ln\frac{15}{17}}{ln\frac{1}{2}}=t$
0.54 years = t

Rate problems : For increasing rate we always add 1 to the b value and for decreasing rate we always subtract b value from 1. For these problems p is always 1.

Example8: A crack in a window grows by 4.5 % every hour. If the crack start at a length of 3 cm, how long will it be in 3 hours.

Solution: Given that Initial amount = 3 cm

And rate =4.5%= 0.045

So b =1+0.045 =1.045

Using formula, $\dpi{120} A=A_{0}\left ( b \right )^{\frac{t}{p}}$

$\dpi{120} A=3\left ( 1.045 \right )^{\frac{3}{1}}$

A = 3.42 cm

Example9: Light passing through murky water loses 30% of its intensity for every meter of water. At what depth will the intensity be half of what it is at the surface?

Solution: Given that water loses 30% of its intensity. Since rate is decreasing so we use b=1-0.3=0.7

And final amount $\dpi{120} A=\frac{1}{2}A_{0}$

$\dpi{120} \frac{1}{2}A_{0}=A_{0}\left ( 0.7 \right )^{\frac{t}{1}}$ here t represents the depth

$\dpi{120} \frac{1}{2}=0.7^{t}$

$\dpi{120} ln\frac{1}{2}=ln0.7^{t}$

ln(0.5) =t ln(0.7)

$\dpi{120} \frac{ln(0.5)}{ln(0.7)}=t$

1.94 m =t

Practice problems:

1. Population of a town doubles every 13 years. If 2330 people were present in year 1990, then find the population in year 2020.

2.A radioactive sample has half life of 2 days. How long will it take for only 1/6^th of the sample to remain?

3.Population of a town halves every 12 years. In how many years will 27% of the population have fled?

4.Light passing through murky water loses 26% of its intensity for every meter of water. At what depth will the intensity be 1/3 of what it is at the surface?

Answers: 1) 11536 people

2) 5.17 days

3) 5.45 years

4) 3.65 m

Applications of exponential functions (Compound Interest)

August 11, 2019/by admin_ct

Formula to calculate compound interest is

$\dpi{150} \mathbf{A= P(1+\frac{i}{n})^{t(n)}}$

Where A= Amount, P= principal sum

i = interest rate in decimals

t= time in years

n =number of times interest is compounded

Have a look at the table showing different values of n for common compounding systems.

Compounding system	Value of n
Annually(once per year)	n=1
Semi-annually(twice in a year)	n=2
Quarterly(4 times in a year)	n=4
Monthly (12 times in a year)	n=12
Daily (365 times in a year)	n =365

Example1: A sum of money $5,000 is invested at 7.2% compounded annually for 4 years. Calculate the amount at the end of 4 years.

Solution: Given that p=5,000 , Since interest is compounded annually so we use n=1

Rate(i) =7.2% =0.072

Time(t)= 4 years

Using formula: $A= P(1+\frac{i}{n})^{t(n)}$

$A= 5000(1+\frac{0.072}{1})^{4(1)}$

$A= 5000\left ( 0.072 \right )^{4}$

A = $6603.12

Example2: A sum of $2,300 is invested at 6% compounded monthly for 7 year. Calculate the interest earned at the end of 7 years.

Solution: Since Interest is compounded monthly so we use n=12 .

Rate(i)= 6%= 0.06

Time(t)= 7 years.

Using formula, $A= P(1+\frac{i}{n})^{t(n)}$

$A= 2300(1+\frac{0.06}{12})^{7(12)}$

$A= 2300(1+0.005)^{84}$

A = 3496.85

Interest earned = Amount – Principal

= 3496.85- 2300= $1196.85

Example3: A sum of $300 is invested at 10% compounded quarterly. How many years must it stay in the bank to double?

Solution: Given principal sum P=$300

And amount(A) = double(600)

Rate(i) = 10% =0.1

Since interest is compounded quarterly so we use n= 4

Using formula, $A= P(1+\frac{i}{n})^{t(n)}$

$600= 300(1+\frac{0.1}{4})^{t(4)}$

$\frac{600}{300}= (1+0.025)^{4t}$

$2= (1.025)^{4t}$

$\ln 2= \ln (1.025)^{4t}$ (taking ln of both sides)

$\ln 2= 4t \ln (1.025)$

$\frac{ln2}{ln(1.025)}= 4t$

28.07 = 4t

7.01 = t

That means money must stay in the bank for 7 years.

Example4: How much money would you need to deposit today at 9% annual interest compounded monthly to have $12000 in the account after 6 years?

Solution: Here we are given amount A=12,000 and we need to find sum invested(p).

Given rate (i) = 9%= 0.09

Time(t)= 6 yrs.

Using formula, $A= P(1+\frac{i}{n})^{t(n)}$

$12000= P(1+\frac{0.09}{12})^{6(12)}$

$12000= P(1+0.0075)^{72}$

12,000 =P(1.712552)

$\frac{12000}{1.712552}= p$

7,007.08 = P

So we need to deposit $7,007.08 today, to get $12000 in 6 years.

Practice problems:

A sum of money $8,000 is invested at 5.6% compounded semi annually for 7 years. Calculate the amount at the end of 7 years.
A sum of $380 is invested at 5% compounded quarterly. How many years must it stay in the bank to triple? Round to nearest year.
How much money would you need to deposit today at 5% annual interest compounded monthly to have $20000 in the account after 9 years?

Answers:

$11775.89
22 years
$12764.49

Solving Exponential Equations

August 10, 2019/by admin_ct

How to solve Exponential Equations

Before learning how to solve exponential function, we should be familiar with basic exponential rules.

$\dpi{120} \mathbf{x^{a}*x^{b}=x^{a+b}}$ powers get added when same bases multiplied
$\dpi{120} \mathbf{\frac{x^{a}}{x^{b}}= x^{a-b}}$ powers get subtracted when same bases divided
$\dpi{120} \mathbf{x^{a}*y^{a}=\left ( xy \right )^{a}}$ having same powers, different bases get multiplied
$\dpi{120} \mathbf{\left ( x^{a} \right )^{b}= x^{ab}}$
$\dpi{120} \mathbf{x^{-k}= \frac{1}{x^{k}}}$ negative powers can be written as fraction

Lets look at one important fact which we are going to use for solving exponential functions,

$\dpi{120} \mathbf{a^{x}=a^{y} \Rightarrow x=y}$

When bases are same, we can equate the exponents(powers).

Lets look at some easy problems first and understand the process with the help of video lesson.

1 Example: Solve the given exponential equation for x.

$\dpi{120} {\color{Red} 2^{2x-1}=2^{x+3}}$

Solution: As we can see, both sides of this equation have same bases, so we can equate the powers and solve for x.

2x-1 = x+3

2x-x = 3+1

x = 4

2Example: Solve the following exponential function for x.

$\dpi{120} {\color{Red} 4^{3x}= 8^{x+1}}$

Solution: Since bases are not same so we have to make them same. We know that both 4 and 8 can be written using exponents of 2.

$\dpi{120} \left ( 2^{2} \right )^{3x}=\left ( 2^{3} \right )^{x+1}$

$\dpi{120} 2^{6x}= 2^{3x+3}$ distribute , 3(x+1)=3x+3

6x = 3x+3 For same bases, power can be equated

3x = 3

x = 1

3 Example: solve for x , $\dpi{120} {\color{Red} 4^{5-9x}= \frac{1}{8^{x-2}}}$

Solution: $\dpi{120} 4^{5-9x}= \frac{1}{8^{x-2}}$

$\dpi{120} 4^{5-9x}= 8^{-(x-2)}$ rewrite fraction using negative exponents

$\dpi{120} \left ( 2^{2} \right )^{5-9x}= \left ( 2^{3} \right )^{-(x-2)}$

$\dpi{120} 2^{2(5-9x)}=2^{3(-x+2)}$ bases made similar

$\dpi{120} 2^{10-18x}=2^{-3x+6}$

10 -18x = -3x +6 having same bases, powers get equated

10-6 = -3x+18x

4 = 15x => x = 4/15

4.Example : Solve the given exponential for x.

$\dpi{120} {\color{Red} 3^{x^{2}}= 3^{6-x}}$

Solution: Nothing much to do as we have already same bases.

So we just equate the exponents and solve for x.

$\dpi{120} x^{2}= 6-x$

$\dpi{120} x^{2}+x-6=0$

(x+3)(x-2) =0

x+3 =0 , x-2 =0

x= -3 , x=2

So far we have worked on examples where we were able to get same bases on both sides of the equation, but it is not always the case. In some exponential equations, we are not given same bases and we are not able to make them same anymore for example $\dpi{120} 5^{x+1}=3^{2}$ . In such cases we work on them taking natural log (ln) of both sides. Lets work on such examples and understand the process with video lesson.

5.Example: Solve the following exponential equations for x. Round your answers to nearest thousandth.

$\dpi{120} {\color{Red} 5^{x+1}=3^{2}}$
$\dpi{120} {\color{Red} 2^{x+1}= 5^{1-2x}}$
$\dpi{120} {\color{Red} 0.3^{1+x}= 1.7^{2x-1}}$
$\dpi{120} {\color{Red} e^{x-5}= 100}$

Solution:1. $\dpi{120} 5^{x+1}=3^{2}$

Taking ln of both sides,

$\dpi{120} \ln 5^{x+1}= \ln 3^{2}$

(x+1)ln5 = ln9 apply power formula of logs

$\dpi{120} x+1 = \frac{ln9}{ln5}$ Please note that $\dpi{100} \frac{ln9}{ln5}\neq ln \left ( \frac{9}{5} \right )$

x+1 = 1.365

x = 0.365

2. $\dpi{120} 2^{x+1}= 5^{1-2x}$

Taking ln of both sides,

$\dpi{120} \ln 2^{x+1}= \ln 5^{1-2x}$

(x+1)ln2 = (1-2x)ln5

xln2 +ln2 = ln5-2xln5

xln2+2xln5 = ln5 –ln2

x(ln2+2ln5)= ln(5/2)

x(ln2+ln5^2 ) = ln(2.5)

x(ln2*25) = ln(2.5)

$\dpi{120} x= \frac{ln(2.5)}{ln(50)} = 0.234$

3. $\dpi{120} 0.3^{1+x}= 1.7^{2x-1}$

Taking ln of both sides,

$\dpi{120} \ln 0.3^{1+x}= \ln 1.7^{2x-1}$

(1+x)ln(0.3) =(2x-1) ln(1.7) Used power rule of log

ln(0.3)+xln(0.3) = 2xln(1.7) –ln(1.7)

ln(0.3) +ln(1.7) = 2xln(1.7)-xln(0.3)

ln(0.3 *1.7) = x[2ln(1.7)-ln(0.3)]

$\dpi{120} \frac{ln(0.51)}{2ln(1.7)-ln(0.3)} = x$

$\dpi{120} \frac{ln(0.51)}{ln(1.7)^{2}-ln(0.3)} = x$

$\dpi{120} \frac{ln(0.51)}{ln\left ( \frac{1.7^{2}}{0.3} \right )}=x$

$\dpi{120} \frac{ln(0.51)}{ln(9.633)}=x$

4. $\dpi{120} e^{x-5}=100$

taking ln of both sides,

$\dpi{120} e^{x-5}=100$

(x-5)ln(e) = ln(100) Since ln and e are inverse of each other so ln(e)= 1

(x-5) = ln(100)

x = 5+ ln(100)

x = 9.605

Practice problems:

Solve the following exponential equations. Round the answer to nearest thousandth wherever possible.

1. $\dpi{120} 3^{2x+1}=81$

2. $\dpi{120} 2^{2x+2}-1 = 15$

3. $\dpi{120} e^{3x}=30$

4. $\dpi{120} \left ( \frac{4}{3} \right )^{1-x}=5^{x}$

Answers:

x=3/2
x=1
x=1.134
x=0.152

Simplify Exponential expressions

August 9, 2019/by admin_ct

How to simplify exponential expressions.

To learn the simplification of expressions with exponents, we should be aware about the rules of exponents first.

$\dpi{120} \mathbf{Product Rule} :\mathbf{x^{a}*x^{b}=x^{a+b}}$ powers get added when same bases multiplied
$\dpi{120} \mathbf{Quotient Rule }: \mathbf{\frac{x^{a}}{x^{b}}=x^{a-b}}$ powers get subtracted when same bases divided
$\dpi{120} \mathbf{Power Rule}: \mathbf{\left ( x^{a} \right )^{b}= x^{ab}}$
$\dpi{120} \mathbf{\mathbf{\mathbf{}}Common Power Rule: \left ( x^{a} \right )\left ( y^{a} \right )= \left ( xy \right )^{a}}$ having same powers, different bases get multiplied
$\dpi{120} \mathbf{Negative Exponent Rule}: \mathbf{x^{-1}=\frac{1}{x}}$ negative powers can be written as fractions
$\dpi{120} \mathbf{x^{-k}=\frac{1}{x^{k}}}$
$\dpi{120} \mathbf{x^{0}=1}$

There may be many ways to simplify an expression using rules of exponents and still ending up with same result (answer). Let’s understand simplification of exponential expressions using following examples.

1. Simplify $\dpi{120} {\color{Red} \left ( 4x^{2} \right )\left ( 3x^{3} \right )}$

$\dpi{120} 4*3*x^{2}*x^{3}$

$\dpi{120} 12x^{2+3} = 12x^{5}$

2. Simplify $\dpi{120} {\color{Red} \left (\frac{24x^{5}}{3x^{2}} \right )}$

$\dpi{120} \left ( \frac{24}{3} \right )\left ( \frac{x^{5}}{x^{2}} \right )= \left (8 \right )(x^{5-2})=8x^{3}$ (write numbers and variables terms together and divide using exponent’s rules)

3. Simplify $\dpi{120} {\color{Red} \left ( 5x^{3} \right )^{4}}$

$\dpi{120} \left ( 5x^{3} \right )^{4}= 5^{4}\left ( x^{3} \right )^{4}= 625x^{12}$ (power get distributed to numerical and variable parts

4. Simplify $\dpi{120} {\color{Red} \left ( x^{-2}y^{2} \right )^{5}\left (x^{5} y \right )^2}$

$\dpi{120} \left ( x^{-2} \right )^{5}\left ( y^{2} \right )^{5}\left ( x^{5} \right )^{2}y^{2}$ (distributing powers to each element)

$\dpi{120} \left ( x^{-10} \right )\left ( y^{10} \right )\left ( x^{10} \right )\left ( y^{2} \right )$

$\dpi{120} \left ( x^{-10+10} \right )\left ( y^{10+2} \right )$ (exponents of same bases combined)

$\dpi{120} x^{0}y^{12}=1 y^{12}=y^{12}$

5. Simplify $\dpi{120} {\color{Red} \left ( \frac{x^{2}y}{z} \right )\left ( \frac{x^{3}z}{y^{3}} \right )}$

$\dpi{120} \left ( \frac{x^{2}y}{z} \right )\left ( \frac{x^{3}z}{y^{3}} \right )$ = $\dpi{120} \left ( x^{2}y \right )\left ( \frac{x^{3}}{y^{3}} \right )$ (cross cancelling z)

$\dpi{120} \left ( x^{2} \right )\left ( x^{3} \right )\left ( \frac{y}{y^{3}} \right )$ ( writing like terms together)

$\dpi{120} \left ( x^{2+3} \right )\left ( y^{1-3} \right )$ (applying rules of exponents)

$\dpi{120} \left ( x^{5} \right )\left ( y^{-2} \right )= \frac{x^{5}}{y^{2}}$

In the following video, we are going to learn how to simplify complex expressions with exponents.

Practice Problems:

Simplify using rules of exponents:

1. $\dpi{120} \left ( x^{2}y \right )^{3}\left ( xy^{2} \right )^{2}$

2. $\dpi{120} \left ( 4x \right )^{3}\left ( 2x \right )^{-5}$

3. $\dpi{120} \frac{2x^{4}y}{\left ( 3xy \right )^{2}}$

4. $\dpi{120} \left ( \frac{x^{2}}{y} \right )^{3}\left ( \frac{y}{x} \right )^{2}$

Answers:

1. $\dpi{120} x^{8}y^{7}$

2. $\dpi{120} \frac{2}{x^{2}}$

3. $\dpi{120} \frac{2x^{2}}{9y}$

4. $\dpi{120} \frac{x^{4}}{y}$

Basics of Exponential and Logarithmic functions

August 9, 2019/by admin_ct

Exponential function:

Any function represented as $\dpi{120} f(x)= a^{x}$ is called exponential function, where a>0 and a≠1 .

Domain of an exponential function is R, set of all real numbers and range is (0,∞ ) because exponential function attains only positive values.

As a>0 and a≠1 so we have the following cases.

Case 1. When a >1

Then exponential function is always an increasing function with y intercept as (0,1).

Case 2. When 0<a<1

Then exponential function is always a decreasing function with same y intercept as(0,1).

Following graphs will help you to observe the similarity and difference between two cases.

Case 3: When a=1

Then $\dpi{120} f(x)=1^{x}=1$ which is a constant function.

Whatever be the value of a, y intercept is always (0,1) is every case.

Logarithmic function:

The function represented as $\dpi{120} f(x)=\log_{a}x$ , a>0, and a ≠1 for x>0 is called logarithmic function.

Log functions are never defined for 0 and negative values. Domain of logarithmic functions is set of all non negative real numbers i.e. (0,∞ ). Range is the set of all real numbers.

As logarithmic and exponential functions are inverse of each other so their domain and range are interchanged.

Depending on the values of a, following are the possible cases.

Case 1. When a>1

Then logarithmic function is increasing function with x intercept as (1,0).

Case 2. When 0<a<1

Then logarithmic function is decreasing function with x intercept same as (1,0).

When base of log is constant e(2.718) instead of a , $\dpi{120} f(x)=\log_{e}x$ then we call the logarithmic function as natural log function f(x)=ln(x).

Following graph will help you to observe the similarity and difference between two cases.

Relationship between logarithmic and exponential function.

We can observe the relationship between exponential and logarithmic function by looking at their graphs together.

Clearly logarithmic and exponential functions are inverse functions!

Logarithmic function is the reflection of exponential function in the line y=x. In other words , axes have been swapped , x become f(x) and f(x) becomes x.

Simplify Radical expressions

August 8, 2019/by admin_ct

Simplify algebraic radical expressions

To learn simplification of radical expressions, we first need to know some basic rules. We can write radicals using exponents as follows:

$\dpi{120} \sqrt{x}= x^{\frac{1}{2}}$

$\dpi{120} \sqrt[3]{x}= x^{\frac{1}{3}}$

$\dpi{120} \sqrt[4]{x}= x^{\frac{1}{4}}$ and so on…..

So basically we can write $\dpi{120} \sqrt[a]{x}= x^{\frac{1}{a}}$

Some more rules :

1. $\dpi{120} \sqrt{\frac{x}{y}}=\frac{\sqrt{x}}{\sqrt{y}}$ or $\dpi{120} \left ( \frac{x}{y} \right )^{a}=\frac{x^{a}}{y^{a}}$

2. $\dpi{120} \sqrt{xy}=\sqrt{x}\sqrt{y}$ or $\dpi{120} \left ( xy \right )^{a}=x^{a}y^{a}$

To simplify nth root radicals, first we write the numerical part in form of their prime factors and then we divide the exponents by nth root (index). Whole numbers go outside radical and remainder remain inside radical. To understand this process lets see few examples.

Example1. Simplify $\dpi{120} {\color{Red} \sqrt[3]{24x^{3}y^{4}}}$

Solution:

Step (i) write numerical part (24) in form of prime factors. And cube root as exponent 1/3

$\dpi{120} \left ( 2^{3}*3*x^{3}*y^{3} \right )^{\frac{1}{3}}$

Step (ii) divide the exponents by 3 write whole numbers outside brackets and remainders inside.

$\dpi{120} 2xy\left ( \3y \right )^{\frac{1}{3}}$ Final answer

Example2. Simplify $\dpi{120} {\color{Red} \sqrt[4]{16x^{8}y^{4}}}$

Step (i) Write nth root in exponent form and numerical part as product of exponential prime factors

$\dpi{120} \left ( 2^{4}x^{8}y^{4} \right )^{\frac{1}{4}}$

Step (ii) Divide all the exponent by 4 . Here remainder is 0 for each one so fourth root goes off.

$\dpi{120} 2x^{2}y$ Final answer

Example3. Simplify $\dpi{120} {\color{Red} \sqrt{\frac{150}{21}}}$

Solution:

$\dpi{120} \sqrt{\frac{150}{21}} = \frac{\sqrt{2*3*5*5}}{\sqrt{3*7}}$

$\dpi{120} \frac{\sqrt{2*3*5^{2}}}{\sqrt{3*7}}$

$\dpi{120} \frac{5*\sqrt{2}*\sqrt{3}}{\sqrt{3}*\sqrt{7}}$

$\dpi{120} \frac{5\sqrt{2}}{\sqrt{7}}$

Other way: Reduce 150/21 to lower term by dividing by 3

$\dpi{120} \sqrt{\frac{150}{21} }= \sqrt{\frac{50}{7}}= \frac{\sqrt{2*5*5}}{\sqrt{7}}= \frac{5\sqrt{2}}{\sqrt{7}}$

Example4. Simplify $\dpi{120} {\color{Red} \sqrt[3]{\frac{27}{8}}}$

Solution: $\dpi{120} \left ( \frac{27}{8} \right )^{\frac{1}{3}}=\frac{27^{\frac{1}{3}}}{8^{\frac{1}{3}}}$

$\dpi{120} \frac{\left ( 3^{3} \right )^{\frac{1}{3}}}{\left ( 2^{3} \right )^{\frac{1}{3}}}= \frac{3}{2}$

Practice problems:

Simplify :

$\dpi{120} \frac{\sqrt{32}}{4}$

2. $\dpi{120} \frac{\sqrt{12}}{\sqrt{3}}$

3. $\dpi{120} \sqrt[5]{32x^{5}y^{10}}$

4. $\dpi{120} \sqrt{18x^{4}y^{6}}$

5. √18 *√2

Answers:

√2
2
$\dpi{120} 2xy^{2}$
$\dpi{120} 3\sqrt{2}x^{2}y^{3}$
6

Operations on radical expressions

August 8, 2019/by admin_ct

Addition , Subtraction of radical expressions

Only like radical can be added or subtracted. So first we should know what are like radicals.

Like Radicals:

These are the expressions which have same radical part (radicand) or they can be simplified further to get same radical parts.

For example √2, 3√2, 10√2 and -5√2 are all like radicals.

On the other hand √32 and √18 are not like radicals but they can be simplified further to get like radicals.

Lets see how √32 and √18 can be simplified.

$\dpi{120} \sqrt{32}= \sqrt{2*4*4}=\sqrt{2*4^{2}}= 4\sqrt{2}$

$\dpi{120} \sqrt{18}= \sqrt{2*3*3}=\sqrt{2*3^{2}}= 3\sqrt{2}$

Now both are like radicals because both have same radical part (√2 ) and they can be added now.

Only the coefficients of like radicals are combined, keeping radical parts as it is.

$\dpi{120} \sqrt{32}+\sqrt{18}= 4\sqrt{2}+3\sqrt{2} = (4+3)\sqrt{2}= 7\sqrt{2}$

Example1. Combine the given radical expressions.

$\dpi{120} {\color{Red} 3\sqrt{5}-\sqrt{2}+\sqrt{5}+5\sqrt{2}}$

Solution: $\dpi{120} 3\sqrt{5}+\sqrt{5}+5\sqrt{2}-\sqrt{2}$ ( write like radical terms together)

$\dpi{120} (3+1)\sqrt{5}+(5-1)\sqrt{2}$ (combined coefficient of like radicals

$\dpi{120} 4\sqrt{5}+4\sqrt{2}$

Some radicals get simplified completely !

Example2. Combine the following radical expression

$\dpi{120} {\color{Red} \sqrt{121}-\sqrt{64}}$

Solution: $\dpi{120} \sqrt{11*11}-\sqrt{8*8}$

$\dpi{120} \sqrt{11^{2}}-\sqrt{8^{2}}$

11 – 8 = 3

Before combining the radical expressions , ensure all radicals are simplified !

Example3. Combine the following radical expression

$\dpi{120} {\color{Red} 5\sqrt{7}-2\sqrt{28}+\sqrt{7}}$

Solution: $\dpi{120} 5\sqrt{7}-2\sqrt{2*2*7}+\sqrt{7}$

$\dpi{120} 5\sqrt{7}-2\sqrt{2^{2}*7}+\sqrt{7}$

$\dpi{120} 5\sqrt{7}-2*2\sqrt{7}+\sqrt{7}$

$\dpi{120} 5\sqrt{7}-4\sqrt{7}+1\sqrt{7}$ [ In absence of any coefficient, 1 can be used just like x can be written as 1x]

$\dpi{120} (5-4+1)\sqrt{7}= 2\sqrt{7}$

But there is no such restriction while multiplying or dividing radicals. We can multiply or divide any radicals together.

For example

Unlike radicals : Like radicals :

√2*√3=√6 √2*√2=2

√5*√7=√35 √7*√7= 7

$\frac{\sqrt{21}}{\sqrt{7}}= \frac{\sqrt{7}*\sqrt{3}}{\sqrt{7}} =\sqrt{3}$ $\frac{2\sqrt{3}}{\sqrt{3}}= 2$

$\frac{\sqrt{45}}{\sqrt{5}}= \frac{\sqrt{9}*\sqrt{5}}{\sqrt{5}}=\sqrt{9}=3$ $\frac{\sqrt{7}}{\sqrt{7}}=1$

Example4. Simplify and combine the following radical expressions

${\color{Red} \sqrt{3}*\sqrt{2}-2\left ( \sqrt{18}\div \sqrt{3} \right )+3\sqrt{6}}$

So0lution:

$\sqrt{3}*\sqrt{2}-2\left ( \sqrt{18}\div \sqrt{3} \right )+3\sqrt{6}$

$\sqrt{6}-2(\sqrt{6})+3\sqrt{6}$

$1\sqrt{6}-2\sqrt{6}+3\sqrt{6}$

$(1-2+3)\sqrt{6}= 2\sqrt{6}$

Practice problems:

1. $\dpi{120} 5\sqrt{3}+\sqrt{3}+5\sqrt{3}-\sqrt{3}$

2. $\dpi{120} \sqrt{75}+\sqrt{48}$

3. $3\sqrt{6}+\sqrt{3}*\sqrt{2}$

4. $5\sqrt{3}*\sqrt{7}-2\sqrt{21}$

Answers:

10√3
9√3
4√6
3√21

Archives

Graphing logarithmic functions

Transformation of log functions

Domain of different log functions:

Intensity of earthquakes and sound loudness

Practice problems:

How to solve Exponential Equations

How to simplify exponential expressions.

Exponential function:

Logarithmic function:

Simplify algebraic radical expressions

Addition , Subtraction of radical expressions

Like Radicals: