Topic Archive - Celestial Tutors

Integration and Accumulation of change

February 1, 2025/by admin_ct

This chapter include:

Approximating integrals using left and right Riemann Sums, mid point rule and Trapezoidal rule
Define definite integral using limits
Accumulation functions, the Fundamental Theorem of Calculus, and definite integrals
Antiderivatives and indefinite integrals
Properties of integrals and integration techniques

Analytical applications of Differentiation

January 25, 2025/by admin_ct

Mathematical Induction

October 11, 2023/by admin_ct

How to prove a statement using mathematical induction?

Proving a statement by mathematical induction is a two-step process. The first step is called the basis step, and the second step is called the inductive step. Base step is generally easy and proved for n=1 or whatever the domain restriction given for n, whereas inductive step require logical thinking and sometimes use some algebraic operations. This process is used to prove variety of statements which are formulated in terms of n, where n is a positive integer.

How many types of mathematical induction is there?

We use two types of mathematical Induction : Weak Induction and Strong induction.

Both are similar in a way that both use the base case but how you prove the inductive step is slightly different for both types. Lets observe the difference.

What is the difference between strong induction and weak induction?

Spot the difference from the point of view of asking a domino why it is falling.

Weak induction: “I’m falling because the domino before me has fallen.”

Strong induction: “I’m falling because all the dominoes before me have fallen.”

Trivially, every statement provable by weak induction is also provable by strong induction, but it is not so obvious whether the converse holds.

Example1 :Prove using mathematical induction that for all n ≥ 1,

${\color{Red} 1^3+2^3+3^3.......+n^3=\left [ \frac{n(n+1)}{2} \right ]^2}$

Lets assume P(n) be the given equation.

$P(n):1^3+2^3+3^3....+n^3=\left [ \frac{n(n+1)}{2} \right ]^2$

Basis step: We need to show that P(1) is true. Which means there is only first term.

$1^3 = \left [ \frac{1(1+1)}{2} \right ]^2$

$1= \left [ \frac{2}{2} \right ]^2$

$1=1$

Therefore, P(1) is true.

Inductive hypothesis: For all integers k≥1, suppose P(k) is true.

$P(k):1^3+2^3+3^3....+k^3=\left [ \frac{k(k+1)}{2} \right ]^2$

Inductive step: We will show that for all integers k≥1, if P(k) is true then P(k+1) is also true.

$P(k+1):1^3+2^3+3^3....+k^3+(k+1)^3=\left [ \frac{(k)(k+1)}{2} \right ]^2+(k+1)^3$ [by substitution from the inductive hypothesis]

Next, we simplify right side.

$\frac{k^2(k+1)^2}{4} +\frac{4}{4}(k+1)^3$ [Make the denominators same]

$\frac{k^2(k+1)^2+4(k+1)^3}{4}$

$\frac{(k+1)^2[k^2+4(k+1)]}{4}$ [ factored out $(k+1)^2$ ]

$\frac{(k+1)^2[k^2+4k+4]}{4}$

$\frac{(k+1)^2(k+2)^2}{4}$

Above expression can be written as a squared function.

$\left [\frac{(k+1)(k+2)}{2} \right ]^2$

Which is actually the right hand side of P(k+1).

Therefore, statement is proved by mathematical induction.

Example 2: Use mathematical induction to prove ${\color{Red} 3^{n}< n!}$ for all integers 𝑛 > 6.

Since n is given greater than 6, so n value used for basis step will be 7.

Lets assume P(n) be the given equation.

$P(n):3^{n}< n!$

Basis step: We need to show that P(7) is true.
$P(7):3^{7}< 7!$

$2187< 5040$ which is true.

That shows P(7) is true.

Inductive hypothesis: For all integers k > 6, suppose P(k) is true.

$P(k):3^{k}< k!$

Inductive step: We will show that for all integers k > 6, if P(k) is true then P(k+1) is also true.

$P(k+1): 3^{k+1} = 3^k*3^{1}$

$3^{k+1}=3 (3^k)$ $3^{k+1}< 3(k!)< (k+1) (k!)$

$3^{k+1}< 3 (k!)$ [ using inductive hypothesis $3^k < k!$ ]

$3^{k+1}< 3(k!)< (k+1) (k!)$ [ 3 will always be less than k+1 as k is greater than 6 so 3 can be replaced with k+1 ]

$3^{k+1}< (k+1) (k!)$

$3^{k+1}< (k+1)!$

Which proves that p(k+1) is true.

Therefore, statement is proved by mathematical induction.

Example 3: Use mathematical induction to prove that log(n!) ≤ nlog(n) for all integers, n≥1.

As given restriction is n≥1 so the n value used for basis step will be 1.

Lets assume P(n) be the given equation.

$P(n): log(n!)\leq nlog(n))$

Basis step: We need to show that p(1) is true.

$P(1): log(1!)\leq 1.log(1)$

log(1)≤1(0)

0 ≤ 0

This shows p(1) is true.

Inductive hypothesis:

For all integers k ≥ 1, suppose P(k) is true.

$P(k): log(k!)\leq klog(k)$

Inductive step:

Next to show that for all integers k ≥1, if P(k) is true then P(k+1) is also true.

$P(k+1):$

$log(k!)\leq klog(k)$ [ from inductive hypothesis ]

Adding log(k+1) to both sides,

$log(k!)+log(k+1)\leq klog(k)+log(k+1)$

$log[(k!)(k+1)]\leq klog(k+1)+log(k+1)$

[ Since log(k) ≤ log(k+1), so log(k) can be replaced with log(k+1) keeping inequality true ]

$log[(k+1)k!]\leq log(k+1)[k+1]$

$log(k+1)!\leq (k+1)log(k+1)$

Which proves that p(k+1) is true.

Therefore, statement is proved by mathematical induction.

Example 4 : Prove by mathematical induction on the positive integers ∀𝑛𝑃(𝑛) where 𝑃(𝑛) is: If 𝐴1, 𝐴2, ⋯ , 𝐴𝑛 and 𝐵 are sets, then $\dpi{100} {\color{Red} \left ( \bigcap_{i=1}^{n} A_i \right )\cup B = \bigcap_{i=1}^{n}(A_i\cup B)}$

Lets assume P(n) be the given equation.

$\dpi{100} P(n) : \left ( \bigcap_{i=1}^{n} A_i \right )\cup B = \bigcap_{i=1}^{n}(A_i\cup B)$

Basis step: We need to show that p(1) is true.

$\dpi{100} P(1) : \left ( \bigcap_{i=1}^{1} A_i \right )\cup B = \bigcap_{i=1}^{1}(A_i\cup B)$

$\dpi{100} A_1 \cup B = (A_i\cup B)$

This shows P(1) is true.

Inductive hypothesis:

For all integers k ≥ 1, suppose P(k) is true.

$\dpi{100} P(k) : \left ( \bigcap_{i=1}^{k} A_i \right )\cup B = \bigcap_{i=1}^{k}(A_i\cup B)$

Inductive step:

Next to show that for all integers k ≥1, if P(k) is true then P(k+1) is also true.

$\dpi{100} P(k+1):$

$\dpi{100} \left ( \bigcap_{i=1}^{k} A_i \right )\cup B = \bigcap_{i=1}^{k}(A_i\cup B)$ [ from inductive hypothesis ]

Adding k+1th term to both sides,

$\dpi{100} \left ( \bigcap_{i=1}^{k} A_i\cup B \right ) \cap (A_{k+1}\cup B)= \bigcap_{i=1}^{k}(A_i\cup B)\cap (A_{k+1}\cup B)$

$\dpi{100} \left ( \bigcap_{i=1}^{k} A_i\cap A_{k+1}\right )\cup B = \bigcap_{i=1}^{k+1}(A_i\cup B)$ [ using distributive law of sets (𝑋 ∩ 𝑌) ∪ 𝑍 = (𝑋 ∪ 𝑍) ∩ (𝑌 ∪ 𝑍)]

$\dpi{100} \left ( \bigcap_{i=1}^{k+1} A_i\right )\cup B = \bigcap_{i=1}^{k+1}(A_i\cup B)$

Which proves that p(k+1) is true.

Therefore, statement is proved by mathematical induction.

Here is an example for proof by strong induction.

Example 5: Consider a proof by strong induction of ∀𝑛𝑃(𝑛) where 𝑃(𝑛) is: If 𝑛 ≥ 12, then 𝑛 cents of postage can be formed by using only 3-cent stamps and 7-cent stamps.

let P(n) : If 𝑛 ≥ 12, then 𝑛 cents of postage can be formed by using only 3-cent stamps and 7-cent stamps.

Since n ≥ 12 , so we prove that P(12), P(13),P(14), P(15) is true for basis step.

P(12) : 4(3) Four 3-cent stamps can make 12 cents of postage.

P(13) : 2(3)+1(7) Two 3-cents stamps and one 7-cent stamp can make 13 cents of postage.

P(14) : 2(7) Two 7-cents stamps can make 14 cents of postage.

P(15): 5(3) Five 3-cents stamps can make 15 cents of postage.

This proves the basis step.

Inductive hypothesis:

For all integers k ≥ 12, suppose P(k) is true.

That means any amount of postage from 12 cents to k cents can be formed by using 3-cents and 7-cents stamps.

Inductive step:

Next to show that for all integers k ≥12, if P(k) is true then P(k+1) is also true. That means if any amount of postage from 12 cents to k cents can be formed by using 3-cents and 7-cents stamps then k+1 cents of postage can also be formed by using 3-cents and 7-cents stamps.

Since P(k) is true by inductive hypothesis, P(k-2) will also be true, where 12≤k-2≤k.

That means postage of k-2 cents can be made using 3 -cents and 7-cents stamps.

P(k+1) = P(k-2 +3)

P(k+1) = P[(k-2)+3]

Which represent postage of k+1 cents of postage can be made using k-2 cents of postage and an additional 3 cent stamp.

Which proves that p(k+1) is true.

Therefore, statement is proved by strong induction.

Practice problems:

Prove the following by principle of mathematical induction.

$\dpi{100} 1+3+3^2+3^3+......+3^{n-1} = \frac{3^n -1}{2}$

2. Prove using mathematical induction that for all n≥4, $\dpi{100} n!\geq n^2$

3. Prove that $\dpi{100} 5^{2n+1}+2^{2n+1}$ is divisible by 7 for all n≥0.

4. Prove the following by principle of mathematical induction.

$\dpi{100} \frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+...+\frac{1}{n(n+1)}= \frac{n}{n+1}$

How to solve linear inequalities with absolute sign?

August 28, 2023/by admin_ct

Linear inequalities with absolute sign are not as easy as simple linear inequalities. They can be divided into 4 cases depending on the inequality sign and positive or negative right side. All these cases are described in a table given below.

Case 1

Case 2

Case 3

Case 4

$\dpi{150} \mathbf{\left | x \right |}< \mathbf{a}$ or

$\dpi{150} \mathbf{\left | x \right |}\leq \mathbf{a}$

$\dpi{150} \mathbf{\left | x \right |}> \mathbf{a}$ or

$\dpi{150} \mathbf{\left | x \right |}\geq \mathbf{a}$

$\dpi{150} \mathbf{\left | x \right |}\leq \mathbf{-a}$

$\dpi{150} \mathbf{\left | x \right |} > \mathbf{-a}$

$\dpi{120} -a < x < a$ or

$\dpi{120} -a\leq x\leq a$

After rewriting like this, we solve this compound inequality using rules of inequality to get x all by itself.

x > a or x < -a

$\dpi{120} x \geq a$ or $\dpi{120} x\leq -a$

After breaking the inequalities like this, expression can be solved further to get x by itself.

Since absolute value is always positive, it can’t be less than or equal to any negative number so this case has no solution.

Since absolute value is always positive ,it would always be greater than any negative number so this case has ‘All real numbers ’ as solution.

Lets work on some examples representing all the 4 cases to understand them better.

Example1. Solve the following inequality

$\dpi{120} {\color{Red} \left | 2x+3 \right |\leq 15}$

Solution: This is of the form $\mathbf{\left | x \right |}\leq \mathbf{a}$ (case 1) , so rewriting the inequality we get,

$\dpi{120} -15\leq 2x+3\leq 15$

-3 -3 -3 subtracting 3 from all sides, we get ,

$\dpi{120} -18 \leq 2x\leq 12$

$\dpi{120} \frac{-18}{2}\leq \frac{2x}{2}\leq \frac{12}{2}$

$\dpi{120} -9\leq x\leq 6$

In interval notation this solution can be written as [-9,6]

Example2. Solve the following inequality and write the solution in interval notation.

3|2x+1| > 9

Solution: First we isolate the absolute part. So divide both sides by 3 we get, |2x+1| > 3

This is of the form $\mathbf{\left | x \right |}> \mathbf{a}$ (case2) , so rewriting the inequality we get,

2x+1 > 3 or 2x+1 < -3

2x > 2 2x < -4

x > 1 or x < -2

Combining these two inequalities by replacing ‘or’ with U (union symbol) to write final answer in interval notation we get,

$\dpi{120} \left ( -\infty ,-2 \right )\cup \left ( 1,\infty \right )$

Example3. Solve the following inequality and write the solution in interval notation.

$\dpi{120} 8+\left | 2x+5 \right |\leq 5{\color{Red} }$

Solution: Subtract 8 from both sides to isolate absolute part we get,

$\dpi{120} \left | 2x+5 \right |\leq -3$

This is of the form $\mathbf{\left | x \right |}\leq \mathbf{-a}$ (case 3).

Since absolute value is always positive, so it can’t be less than or equal to any negative number. Therefore this inequality has No Solution.

Example4. Solve the following inequality and write the solution in interval notation.

$\dpi{120} 8+\left | 2x+5 \right |>5$

Solution: Subtract 8 from both sides to isolate absolute part we get,

$\dpi{120} \left | 2x+5 \right |> -3$

This is of the form $\mathbf{\left | x \right |} > \mathbf{-a}$ (case 4).

Since absolute value is always positive, so it is always greater than any negative number. Therefore this inequality has ‘All Real numbers ’ as solution which can be written in interval notation as, (-∞,∞)

Inequalities with absolute sign having variables on both sides:

Inequalities having more than one absolute sign or having variable on both sides, are solved using different approach. We get the intervals on a number line according to expression inside absolute signs and then solve inequalities for each interval. Lets work on some examples to understand this process better.

Example5. Solve the given inequality and write the answer in interval notation.

|x-1|+|x-2| ≥ 4

Solution: First we set the expressions inside absolute signs =0 to get points on number line.

So x-1=0 => x=1 and x-2=0 => x=2

Using these two points, we get the intervals on number line as (-∞,1) ,(1,2) and (2,∞). Here we also make use of definition of absolute function.

$\dpi{120} \left | x-1 \right |= \left\{\begin{matrix} -(x-1) & x < 1 \\ (x-1) &x\geq 1 \end{matrix}\right.$ $\dpi{120} \left | x-2 \right |= \left\{\begin{matrix} -(x-2) & x < 2 \\ (x-2) &x\geq 2 \end{matrix}\right.$

For interval (-∞,1) we have the inequality as,

-(x-1)-(x-2) ≥ 4

-x+1-x+2 ≥ 4

-2x +3 ≥ 4

-2x ≥ 1

x ≤ -½ —–(i)

For interval (1,2) we have the inequality as,

(x-1) –(x-2) ≥ 4

x-1-x+2 ≥ 4

1 ≥ 4 (which is absurd )

For interval (2,∞), we have the inequality as,

(x-1) +(x-2) ≥ 4

2x -3 ≥ 4

2x ≥ 7

$\dpi{120} x\geq \frac{7}{2}$ ——–(ii)

Combining results (i) and (ii) we get the final solution in interval form as, (-∞ , -½] U [ 7/2 ,∞)

Example6. Solve the inequality |2x-3| > x-1

Solution: Taking positive and negative cases separately,

-(2x-3) > x-1 or 2x-3 > x-1

-2x+3 > x-1 2x-x > -1+3

-2x-x > -1-3 x > 2

-3x > -4

x < 4/3

Combining these two inequalities, we get the final answer in interval form as, (-∞, 4/3) U (2,∞)

Practice problems:

Solve the following inequalities and write the solution in interval form.

1) |3x-2| ≤ ½

2) |4-x| +1 > 3

3) |x-1|+|x-2|+|x-3|≥ 6

4) 4+|x-3| < 1

Answers:

1) [1/2 , 5/6]

2) (-∞,2) U(6,∞)

3) (-∞,0] U [4,∞)

4) No solution

How to solve linear inequalities with radicals ?

August 28, 2023/by admin_ct

Linear inequalities with radicals

While dealing with inequalities having square root (radical) , we also need to consider the domain of radical expressions. We take into consideration both the solutions, one which we get after solving inequality by squaring both sides and other by setting radicand ≥ 0. lets work on some examples to understand this process better.

Example1. Solve the following inequality and write the solution in interval form.

${\color{Red} \sqrt{x-1}+2\leq 5}$

Solution: $\sqrt{x-1}+2\leq 5$

$\sqrt{x-1}\leq 3$

Squaring both sides, $(\sqrt{x-1})^{2}\leq 3^{2}$

x – 1 ≤ 9

x ≤ 10 ——(i)

Since radicals are not defined for negative values so radicand must be positive. Therefore, x-1 ≥ 0

=> x ≥ 1 ——–(ii)

Combining the solutions (i) and (ii), we get final solution as,

1 ≤ x ≤ 10 => [1 ,10]

Example2. Solve the following inequality and write the solution in interval form.

${\color{Red} 4-\sqrt{x-3} \geq -2}$

Solution: $4-\sqrt{x-3}\geq -2$ Also, $x-3 \geq 0$

$-\sqrt{x-3}\geq -6$ x ≥ 3

$\sqrt{x-3}\leq 6$ (multiplied with -1 and inequality sign changed)

squaring both sides, $(\sqrt{x-3})^{2}\leq 6^{2}$

x -3 ≤ 36

x ≤ 39

combining two solutions we get, 3 ≤ x ≤ 39

Final answer in interval form [3,39]

Example3.Solve the following inequality and write the solution in interval form.

$\dpi{120} {\color{Red} \sqrt[2]{x}\leq \sqrt[3]{x}}$

Solution: We can rewrite the given inequality as,

$\dpi{120} x^{1/2} \leq x^{1/3}$

Since LCM of denominators 2 and 3 is 6 so we multiply exponents of both sides with 6 and get,

$\dpi{120} \left ( x^{1/2} \right )^{6}\leq \left ( x^{1/3} \right )^{6}$ => $\dpi{120} x^{3}\leq x^{2}$

$\dpi{120} x^{3}-x^{2}\leq 0$

$\dpi{120} x^{2}(x-1)\leq 0$

As $\dpi{120} x^{2}$ can never be negative so x-1 ≤ 0

x≤ 1 —— (i)

Also $\dpi{120} x^{1/2}$ , being an even radical is never defined for negative values which restrict the given solution to x ≥ 0 —— (ii)

So final solution, after combining (i) and (ii) is given as,

0≤x≤1 => [0,1]

Example4. Solve the inequality $\dpi{120} {\color{Red} \sqrt{x}\geq 2 \sqrt[4]{x}}$

Solution: Rewriting the given inequality as,

$\dpi{120} x^{1/2} \geq 2 x^{1/4}$

Since lcm of denominators 2 and 4 is 4, So raising exponents on both sides by 4 and we get,

$\dpi{120} \left ( x^{1/2} \right )^{4}\geq (2 \left ( x^{1/4} \right ))^{4}$

$\dpi{120} x^{2}\geq 2^{4}x$

$\dpi{120} x^{2}\geq 16x$

$\dpi{120} x^{2}-16x\geq 0$

x ( x-16) ≥ 0

As we know that even radicals are not defined for negative values which restrict domain to x ≥ 0,

Also, x-16≥0 => x≥ 16

So final solution is given as, [16,∞)

Practice problems:

Solve the following inequalities and write the answer in interval form.

$\dpi{120} \sqrt[4]{x}> \sqrt[3]{x}$
$3\sqrt{2x-1}+6\leq 15$
$\dpi{120} \sqrt{c+4}-3\geq 3$
$\dpi{120} -3\sqrt{11r+3}> -15$

Answers:

(0,1)
[1/2, 5]
[32,∞)
( -3/11 , 2)

How to solve linear inequalities ?

August 28, 2023/by admin_ct

Solving linear inequalities is similar to solving linear equations. All the rules and facts are same as for linear equation , only exception is that whenever we multiply or divide any inequality with a negative number, its sign get reversed. That means < sign get changed to > and viceversa.

Here are few examples to understand the process.

Example1. Solve the following inequality.

2(x-3) > 10

Solution: $\dpi{120} \frac{2(x-3)}{2}> \frac{10}{2}$

(x-3) > 5

X > 5+3

X > 8

Now we work on same example but with a negative sign and see how it effect the solution.

Example2. Solve the following inequality.

-2(x-3) > 10

Solution: To get rid of -2 , we divide both sides by -2 and therefore inequality sign get reversed.

$\dpi{120} \frac{-2(x-3)}{-2}< \frac{10}{-2}$

(x-3) < -5

X < -5+3 => x < -2

Representing the solution of an inequality : Solution of an inequality can be represented in two ways. One as an inequality and other as interval notation. To represent the solution in interval notation we need to be familiar with some rules.

Rules to convert the inequality in interval notation:

1) In interval notation smaller number is always written towards left (first place) and larger number is written towards right(second place). This rule would be helpful in solving double inequalities.

2) Solution having only < or > sign is represented with open brackets ( ) which means end points are not included

3) The solution having or is represented with closed brackets [ ] which means end points are included.

4) We always use parenthesis ( ) with infinity.

Here is a beautiful tabular representation of all these rules.

Representing the solution of inequality on a number line :

Inequality	Interval Notation	Number line representation
a<x<b	(a,b)
a≤x≤b	[a,b)
a<x≤ b	(a,b]
a≤x ≤b	[a,b]
X<b	(-∞ ,b)
x>a	(a, $\bg_white \large \mathbf{\infty}$ )
x ≤ b	(- $\dpi{120} \infty$ , b]
x ≥ a	[a, $\dpi{120} \infty$ )

Example3. Solve the following inequality and represent the solution as interval notation.

12-(2t+1) ≥ 2(t-5)

Solution: First we remove parenthesis , for that we distribute – sign on left and 2 on right side of the inequality.

12 -2t-1 $\dpi{120} \geq$ 2t-10

-2t -2t $\dpi{120} \geq$ -10-12+1 (combining and rearranging like terms)

-4t $\dpi{120} \geq$ -21

$\frac{-4t}{-4}\leq \frac{-21}{-4}$ (inequality reversed when divided by negative number)

$t \leq \frac{-21}{4}$

In interval notation answer can be written as,

$\dpi{100} \left ( -\infty ,\frac{-21}{4} \right )$

Example4. Solve the following inequality and write the answer in interval notation. Also represent it on number line.

$\dpi{100} 7+\frac{1}{5}\left ( x-10 \right )\geq \left ( x+1 \right )$

Solution: Distributing 1/5 we get,

$\dpi{100} 7+\frac{x}{5}-2\geq \ x+1$

$\dpi{100} \frac{x}{5}-x\geq 1-7+2$

$\dpi{100} \frac{-4x}{5}\geq -4$

Multiply both sides with -5/4 to get x by itself,

$\dpi{100} \frac{-5}{4}*\frac{-4x}{5}\leq -4*\frac{-5}{4}$ (inequality reversed when multiplied by negative number)

x $\dpi{120} \leq$ 5

Interval notation: (- $\dpi{120} \infty$ , 5]

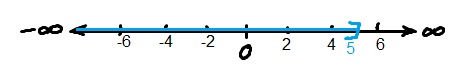
How to solve Double inequality: Solving double inequality is similar to solving single inequality but here we don’t move the variable to one side and numbers to other side as we do in solving single inequality. Our target is to get x all by itself and to get that,we use same operation to both sides. That means if we add or subtract something to middle x term, we do the same operation to left and right side terms too.

Example5. Solve the following inequality and represent the solution in interval notation.

7 < 5+2x < 1

Solution: 7 < 5+2x < 1

-5 -5 -5 (subtracting 5 from all sides)

2 < 2x < -4

$\dpi{120} \frac{2}{2}< \frac{2x}{2}< \frac{-4}{2}$

1 < x < -2

As per rules of writing interval notations, smaller number should be written first, so this inequality can be rewritten as,

-2 < x < 1

Which can be further written in interval notation as (-2,1)

Example6. Solve the given compound inequality and represent the solution in interval notation. Also represent the solution on number line. -10 < -5(x+2) $\dpi{120} \leq$ 6

Solution: -10 < -5x-10 $\dpi{120} \leq$ 6 (distributed -5) $\dpi{100} 7+\frac{1}{5}\left ( x-10 \right )\geq \left ( x+1 \right ){\color{Red} }$

-10 < -5x-10 $\dpi{120} \leq$ 6

+10 +10 +10

0 < -5x $\dpi{120} \leq$ 16

$\dpi{120} \frac{0}{-5}> \frac{-5x}{-5}\geq \frac{16}{-5}$

$\dpi{100} 0> x\geq \frac{-16}{5}$

Writing this solution in proper format , we get interval notation as

$\dpi{100} [\frac{-16}{5},0)$ => [-3.2 ,0)

Practice problems:

Solve the following inequalities and represent the solutions in interval notation.

3(2x-5) $\dpi{120} \leq$ -15
-2(x+1) > 8-(x+5)

Solve the following compound inequalities and represent the solution on number line.

-5 $\dpi{120} \leq$ 2x-1 $\dpi{120} \leq$ 3
9 $\dpi{120} \geq$ 3(x-1) $\dpi{120} \geq$ -12

Answers:

(- $\dpi{120} \infty$ ,0]
(- $\dpi{120} \infty$ , -5)
[-2,2]
[-3,4]

Square root and Approximations

August 25, 2023/by admin_ct

Square root and Approximations

To know about approximating square roots, first we should learn perfect squares because they are interrelated. Here is a table of perfect squares and square roots.

$\dpi{120} 1^{2}=1$	$\dpi{120} \sqrt{1} =1$
$\dpi{120} 2^{2}=4$	$\dpi{120} \sqrt{4} =2$
$\dpi{120} 3^{2}=9$	$\dpi{120} \sqrt{9} =3$
$\dpi{120} 4^{2}=16$	$\dpi{120} \sqrt{16} =4$
$\dpi{120} 5^{2}= 25$	$\dpi{120} \sqrt{25} =5$
$\dpi{120} 6^{2}= 36$	$\dpi{120} \sqrt{36} =6$
$\dpi{120} 7^{2}= 49$	$\dpi{120} \sqrt{49} =7$
$\dpi{120} 8^{2}= 64$	$\dpi{120} \sqrt{64} =8$
$\dpi{120} 9^{2}= 81$	$\dpi{120} \sqrt{81} =9$
$\dpi{120} 10^{2}=100$	$\dpi{120} \sqrt{100} =10$
$\dpi{120} 11^{2}= 121$	$\dpi{120} \sqrt{121}= 11$
$\dpi{120} 12^{2}=144$	$\dpi{120} \sqrt{144}=12$
$\dpi{120} 13^{2}=169$	$\dpi{120} \sqrt{169} = 13$
$\dpi{120} 14^{2}=196$	$\dpi{120} \sqrt{196}= 14$
$\dpi{120} 15^{2}= 225$	$\dpi{120} \sqrt{225}=15$
$\dpi{120} 16^{2}=256$	$\dpi{120} \sqrt{256}=16$
$\dpi{120} 17^{2}=289$	$\dpi{120} \sqrt{289} = 17$
$\dpi{120} 18^{2}=324$	$\dpi{120} \sqrt{324} = 18$
$\dpi{120} 19^{2}= 361$	$\dpi{120} \sqrt{361} = 19$
$\dpi{120} 20^{2}=400$	$\dpi{120} \sqrt{400} = 20$

This way you can learn the square roots upto 50. Lets discuss the process of approximating square roots now.

There are many ways to approximate the square roots. The one which we are going to discuss, is the easiest and quicker one. Here are the steps:

1)First find the nearest perfect squares, in which the sqrt lie between.

2) Lets assume the sqrt number to be approximated as S, smaller perfect square as N and larger perfect square as N+1 such that

$\dpi{120} N^{2}< S < (N+1)^{2}$

Then the approximation A is given by the following formula.

$\dpi{120} \mathbf{A=N+\left ( \frac{S-N^{2}}{2N+1} \right )}$

Lets work on some examples to understand the process

Example1. Approximate √34 to one decimal place.

Solution: √34 lie between √25 and √36 which are nearest perfect squares so,

$\dpi{120} \sqrt{25}< \sqrt{34}< \sqrt{36}$

$\dpi{120} 5^{2}< 34 < 6^{2}$

Here S= 34 , N=5 , N+1=6

Using formula, $\dpi{120} A=N+\left ( \frac{S-N^{2}}{2N+1} \right )$

$\dpi{120} A=5+\left ( \frac{34-5^{2}}{2*5+1} \right ) = 5 +\frac{9}{11} = 5.8$

Example2. Approximate √70 to one decimal place.

Solution: √70 lie between √64 and √81 which are the nearest perfect squares so,

$\dpi{120} \sqrt{64}< \sqrt{70}< \sqrt{81}$

$\dpi{120} 8^{2}< 70 < 9^{2}$

Here S= 70 , N=8 , N+1=9

Using formula, $\dpi{120} A=N+\left ( \frac{S-N^{2}}{2N+1} \right )$

$\dpi{120} A=8+\left ( \frac{70-8^{2}}{2*8+1} \right ) = 8 +\frac{6}{17} = 8.4$

The method discussed above gives you sqrt approximation upto one decimal place.

Second method: If you are on time constraint For SAT, ACT or any other test and you are given choices then we can fairly guess the right answer by finding the nearest perfect squares and distance of sqrt from the nearest perfect square.

For example we need to approximate √70 which lie between perfect squares 64 and 81.

$\dpi{120} \sqrt{64}< \sqrt{70}< \sqrt{81}$

$\dpi{120} 8< \sqrt{70}< 9$

Distance between 70 and its nearest perfect square 64 is 6 which is less then halfway (72.5) that means √70 would be approximated to a value less than 8.5 but closer to 8.5. Based on this observation we can guess the right answer out of the following options.

a) 7.8

b) 8.6

c) 8.4

d) 8.9

We are pretty sure about the right answer to be 8.4 because Only this option is less than 8.5 and closer to it.

To approximate √74 we choose 8.6 because 74 is more than halfway 72.5 and closer to it.

To approximate √ 79 we choose 8.9 because 79 is more than halfway 72.5 and more closer to 81 so it would be approximated closer to 9.

So when we are on a time constraint and have multiple choices , we can use above estimation process.

First method gives you the exact approximation upto one decimal place , second method also gives a pretty good estimation within seconds.

You can always check your results by using calculators.

Scientific and Standard notations

August 25, 2023/by admin_ct

Ptolemy’s Theorem

August 18, 2023/by admin_ct

In a cyclic quadrilateral, the sum of product of two pairs of opposite sides equals the product of its diagonals.

$\dpi{120} AB\times CD + BC\times AD = AC\times BD$

Lets work on some examples on Ptolemy’s theorem.

What is the length of chord $\dpi{100} {\color{Red} \overline{AC}}$ ? Explain your answer.

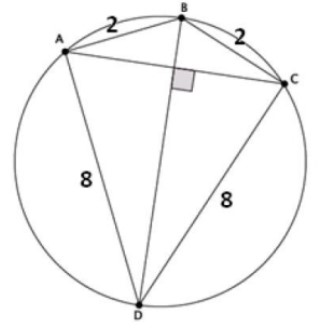
To solve this problem, we will use Ptolemy’s theorem.

For that we need to find other diagonal BD first using Pythagorean. So two cases arise here.

Case 1: BD is a diameter passing through center of circle.

Then ABD and BCD both are right triangles using Thales theorem.

$\therefore \angle BAD=\angle BCD = 90$

$(BD)^{2}=(AB)^{2}+(AD)^{2}$ [ applying Pythagorean in right triangle BAD ]

$(BD)^{2}=(2)^{2}+(8)^{2}$

$BD=\sqrt{4+64}$

$BD=\sqrt{68}$

Case 2: BD is NOT a diameter.

Then ΔBAD and ΔBCD are congruent by SSS rule of congruency.

AB = BC = 2 [ given equal sides ]

AD = CD = 8 [ given equal sides ]

BD = BD [ common sides ]

$\therefore \Delta BAD = \Delta BCD$ [ by SSS rule of congruency ]

$\therefore \angle BAD = \angle BCD$ [ by CPCTE ]

Since ABCD is a cyclic quadrilateral , therefore sum of its apposite angles would be 180.

Here angles BAD and BCD are opposite angles of a cyclic quadrilateral and both are equal so each must be 90.

Therefore we can apply Pythagorean in any of the triangles to find side BD.

Once we have BD, we can apply Ptolemy’s theorem.

so we have,

$AB\times CD + BC\times AD = AC\times BD$ [ by Ptolemy’s theorem ]

$2\times 8 + 2\times 8 = AC\times \sqrt{68}$

$32 = AC\times \sqrt{68}$

$\frac{32}{\sqrt{68}} = AC$

$AC = \frac{32}{2\sqrt{17}}$

$AC = \frac{16}{\sqrt{17}}=\frac{16\sqrt{17}}{17}$

An equilateral triangle is inscribed in a circle, If P is a point on the circle, What does Ptolemy’s theorem have to say about the distances from this point to three other vertices ?

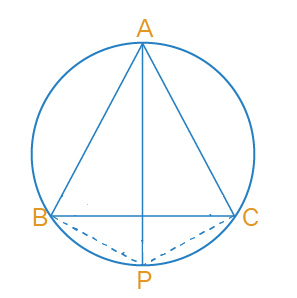
Lets join vertices B and C with point P. Now ABPC makes a cyclic quadrilateral. Ptolemy’s theorem can be applied here.

$\dpi{100} \therefore BC\times AP= AB\times PC+AC\times BP$

Since ΔABC is given equilateral, so we have its all three sides equal. Lets assume each side as x.

AB = BC = CA = x

Now replace AB, BC and CA with x in the first expression, and we get it as,

$\dpi{100} xAP= x PC+x BP$

Dividing both sides of this equation by x, we get

$\dpi{100} AP= PC+ BP$

Which can be summarized as under,

Larger distance, which is the distance from point P to vertex A is equal to sum of smaller distances to other two vertices.

Kite ABCD is inscribed in a circle. The kite has an area of 108 in².The ratio of lengths of non congruent adjacent sides is 3:1 . What is the perimeter of this kite?

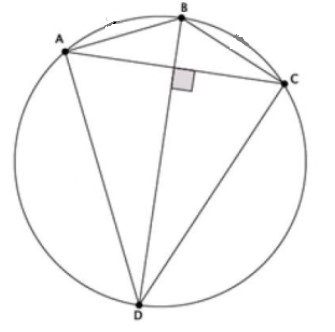
To find side length of each side of kite, we make use of Ptolemy’s theorem. But before that we need to use area of kite formula.

$\dpi{100} A= \frac{1}{2}\times AC\times BD$

$\dpi{100} 108= \frac{1}{2}\times AC\times BD$

$\dpi{100} 2\times 108= AC\times BD$

$\dpi{100} 216= AC\times BD$

Given ratio of lengths of non congruent adjacent sides = 3:1

Then we can write non congruent sides AD and AB as 3x and x, where x is the common ratio.

Using Ptolemy’s theorem,

$\dpi{100} AB\times CD + BC\times AD = AC\times BD$

$x\times 3x + x\times 3x = 216$

$3x^{2} + 3x^{2} = 216$

$6x^{2} = 216$

$x^{2} = \frac{216}{6}=36$

$x =\pm \sqrt{36}=\pm 6$

x = 6 , accepting only positive value as distance measurements can never be negative.

So all the sides of Kite are given as,

3x = 3(6)= 18

x= 6

and perimeter of kite is given as,

18+6+18+6 = 48 inches

Practice problems:

Draw a regular pentagon of side length 1 in a circle. Let b be the length of its diagonals. What does Ptolemy’s theorem say about quadrilateral formed by four of the vertices of Pentragon ?
Prove Pythagorean theorem using Ptolemy’s theorem.

Equation of circle (general form)

August 14, 2023/by admin_ct

The general form of the equation of circle is:

x² + y² + 2gx + 2fy + c = 0.

Its center and radius is given as :

Center : (-g,-f)

radius r :

$\sqrt{(g^{2} + f^{2} - c)}$

Using above expression , we can tell some more information about circle ,

If $g^{2}+f^{2}>c$ Then it is a real circle with radius r.

If $g^{2}+f^{2}= c$ Then the circle coincides with its center and it would be just a point or called point circle.

If $g^{2}+f^{2}< c$ Then this circle won’t be possible as its radius would be an imaginary number. So the solution is empty set.

Identify the center and radius of a circle with the following equation.

${\color{Red} x^{2}+y^{2} -12x-16y+19 =0 }$

First, compare the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get, 2g= -12

g = -6 ⇒ -g = 6

and 2f = -16

f = -8 ⇒ -f = 8

Therefore center of circle is given as : (6,8)

and radius is given as,

$r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{6^{2}+8^{2}-19}$

$r=\sqrt{100-19} =\sqrt{81}=9$

Find center and radius of a circle for the given equation using two ways. Firstly using general formula, secondly using standard formula by completing square method.

${\color{Red} x^{2}+4x +y^{2} -12y -41 =0 }$

Using general formula , we compare the given equation with general equation

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 4 ⇒ g= 2

and

2f = -12 ⇒ f = -6

Therefore, we get center of circle as (-g, -f) = (-2,6)

and radius as $r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{(-2)^{2}+6^{2}+41}$

$r=\sqrt{81}=9$

Using standard form , we complete the squares for both x and y terms.

$x^{2}+4x +y^{2} -12y -41 =0$

$x^{2}+4x +y^{2} -12y =41$

$x^{2}+4x {\color{Red} +4} +y^{2} -12y {\color{Red} +36} =41{\color{Red} +4+36}$ [ added 4 and 36 on both sides to complete perfect squares ]

$(x^{2}+4x +4) +(y^{2} -12y +36) =41 +4+36$

$(x+2)^{2} +(y-6)^{2} = 81$

Comparing it with standard form:

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

we get center (h,k) = (-2,6)

and radius r²= 81 ⇒ r= 9

Stella says the equation ${\color{Red} x^{2}-8x+y^{2}+2y= 5 }$ has a center (4,-1) and radius of 5. Is she correct? why or why not ?

We can find its center using either of the above mentioned two methods.

Lets use completing square method.

$x^{2}-8x+{\color{Red} 16}+y^{2}+2y{\color{Red} +1}= 5 {\color{Red} +16+1}$ [ added 16 and 1 on both sides to complete the squares]

$(x^{2}-8x+ 16)+(y^{2}+2y +1)= 22$

$(x-4)^{2}+(y+1)^{2}= 22$

Comparing it with standard form, we get center as (4,-1)

and radius r = √22

Stella is correct that center is (4,-1) . However she didn’t find the radius correctly. Correct radius is √22 not 5.

Identify the graphs of the following equations as a circle, a point or an empty set.

a) ${\color{Red} x^{2}+y^{2}+4x=0}$

To answer this question , it would be better to use general form and above mentioned rules for radius.

Rewriting the given equation in general form we get,

$x^{2}+y^{2}+4x+0y=0$

Now comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 4 ⇒ g= 2

2f = 0 ⇒ f =0

c= 0

Using formula for radius ,

$r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{2^{2}+0^{2}-0}= 2$

That means this is a real circle with radius 2.

b) ${\color{Red} x^{2}+y^{2}+6x-4y +15= 0 }$

Comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 6 ⇒ g= 3

2f = -4 ⇒ f = -2

c= 15

Using formula for radius ,

$r=\sqrt{3^{2}+(-2)^{2}-15}$

$r=\sqrt{13-15}=\sqrt{-2}$

Since radius is an imaginary number , that means this circle not possible and its graph would be empty set.

c) ${\color{Red} x^{2}+y^{2}+6x-4y +13= 0 }$

Comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 6 ⇒ g= 3

2f = -4 ⇒ f = -2

c= 13

Using formula for radius ,

$r=\sqrt{3^{2}+(-2)^{2}-13}$

$r=\sqrt{13-13}= 0$

Since radius is 0 so this would be a point .

Practice problems:

Find center and radius of a circle for the given equation using two ways. Firstly using general formula, secondly using standard formula by completing square method.

a) $x^{2}+y^{2}+2y= 5$

b) $x^{2}+4x +y^{2}+6y= 3$

Identify the graphs of the following equations as a circle, a point or an empty set.

a) $x^{2}+y^{2}+2y= 5$

b) $x^{2}+4x +y^{2}+6y+13=0$

c) $x^{2}+10x +y^{2}+2y+36=0$

Archives

How to prove a statement using mathematical induction?

How many types of mathematical induction is there?

What is the difference between strong induction and weak induction?

Inequalities with absolute sign having variables on both sides:

Practice problems:

Square root and Approximations

Practice problems:

x2 + y2 + 2gx + 2fy + c = 0.

Practice problems:

x² + y² + 2gx + 2fy + c = 0.