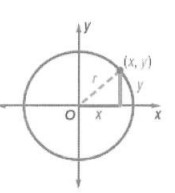
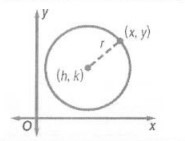
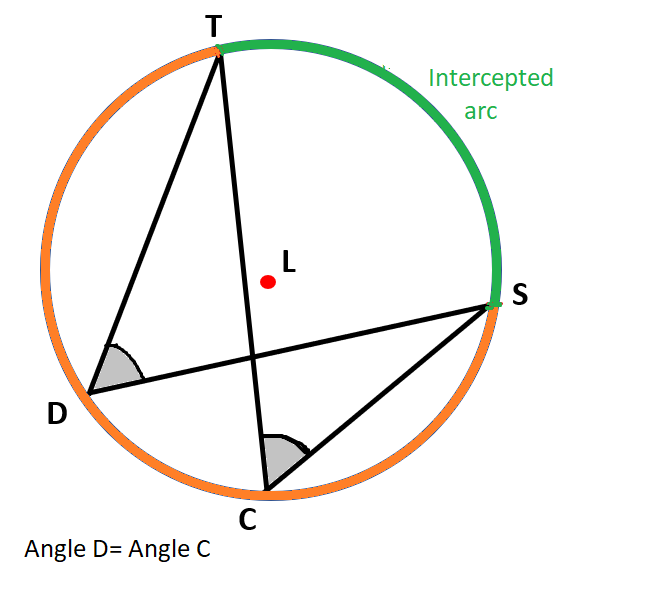
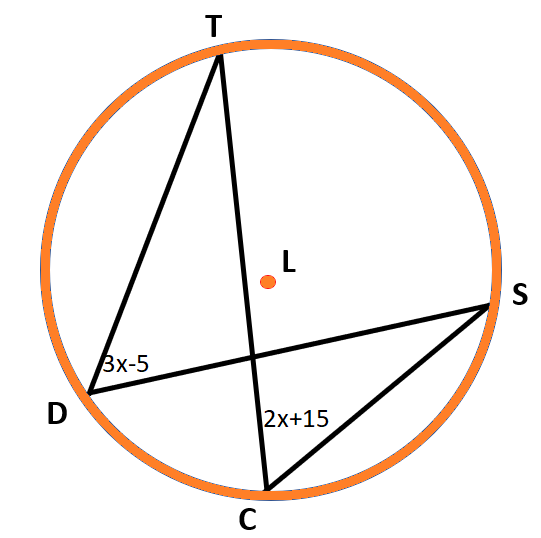
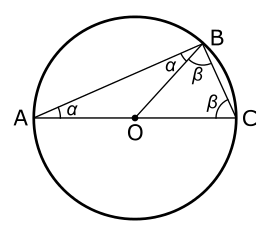
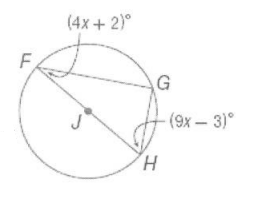
Topic Archive - Page 2 of 7 - Celestial Tutors

Equation of circle (general form)

August 14, 2023/by admin_ct

The general form of the equation of circle is:

x² + y² + 2gx + 2fy + c = 0.

Its center and radius is given as :

Center : (-g,-f)

radius r :

$\sqrt{(g^{2} + f^{2} - c)}$

Using above expression , we can tell some more information about circle ,

If $g^{2}+f^{2}>c$ Then it is a real circle with radius r.

If $g^{2}+f^{2}= c$ Then the circle coincides with its center and it would be just a point or called point circle.

If $g^{2}+f^{2}< c$ Then this circle won’t be possible as its radius would be an imaginary number. So the solution is empty set.

Identify the center and radius of a circle with the following equation.

${\color{Red} x^{2}+y^{2} -12x-16y+19 =0 }$

First, compare the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get, 2g= -12

g = -6 ⇒ -g = 6

and 2f = -16

f = -8 ⇒ -f = 8

Therefore center of circle is given as : (6,8)

and radius is given as,

$r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{6^{2}+8^{2}-19}$

$r=\sqrt{100-19} =\sqrt{81}=9$

Find center and radius of a circle for the given equation using two ways. Firstly using general formula, secondly using standard formula by completing square method.

${\color{Red} x^{2}+4x +y^{2} -12y -41 =0 }$

Using general formula , we compare the given equation with general equation

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 4 ⇒ g= 2

and

2f = -12 ⇒ f = -6

Therefore, we get center of circle as (-g, -f) = (-2,6)

and radius as $r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{(-2)^{2}+6^{2}+41}$

$r=\sqrt{81}=9$

Using standard form , we complete the squares for both x and y terms.

$x^{2}+4x +y^{2} -12y -41 =0$

$x^{2}+4x +y^{2} -12y =41$

$x^{2}+4x {\color{Red} +4} +y^{2} -12y {\color{Red} +36} =41{\color{Red} +4+36}$ [ added 4 and 36 on both sides to complete perfect squares ]

$(x^{2}+4x +4) +(y^{2} -12y +36) =41 +4+36$

$(x+2)^{2} +(y-6)^{2} = 81$

Comparing it with standard form:

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

we get center (h,k) = (-2,6)

and radius r²= 81 ⇒ r= 9

Stella says the equation ${\color{Red} x^{2}-8x+y^{2}+2y= 5 }$ has a center (4,-1) and radius of 5. Is she correct? why or why not ?

We can find its center using either of the above mentioned two methods.

Lets use completing square method.

$x^{2}-8x+{\color{Red} 16}+y^{2}+2y{\color{Red} +1}= 5 {\color{Red} +16+1}$ [ added 16 and 1 on both sides to complete the squares]

$(x^{2}-8x+ 16)+(y^{2}+2y +1)= 22$

$(x-4)^{2}+(y+1)^{2}= 22$

Comparing it with standard form, we get center as (4,-1)

and radius r = √22

Stella is correct that center is (4,-1) . However she didn’t find the radius correctly. Correct radius is √22 not 5.

Identify the graphs of the following equations as a circle, a point or an empty set.

a) ${\color{Red} x^{2}+y^{2}+4x=0}$

To answer this question , it would be better to use general form and above mentioned rules for radius.

Rewriting the given equation in general form we get,

$x^{2}+y^{2}+4x+0y=0$

Now comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 4 ⇒ g= 2

2f = 0 ⇒ f =0

c= 0

Using formula for radius ,

$r=\sqrt{g^{2}+f^{2}-c}$

$r=\sqrt{2^{2}+0^{2}-0}= 2$

That means this is a real circle with radius 2.

b) ${\color{Red} x^{2}+y^{2}+6x-4y +15= 0 }$

Comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 6 ⇒ g= 3

2f = -4 ⇒ f = -2

c= 15

Using formula for radius ,

$r=\sqrt{3^{2}+(-2)^{2}-15}$

$r=\sqrt{13-15}=\sqrt{-2}$

Since radius is an imaginary number , that means this circle not possible and its graph would be empty set.

c) ${\color{Red} x^{2}+y^{2}+6x-4y +13= 0 }$

Comparing the given equation with general equation of circle :

$x^{2}+y^{2} +2gx+2fy+c =0$

we get,

2g = 6 ⇒ g= 3

2f = -4 ⇒ f = -2

c= 13

Using formula for radius ,

$r=\sqrt{3^{2}+(-2)^{2}-13}$

$r=\sqrt{13-13}= 0$

Since radius is 0 so this would be a point .

Practice problems:

Find center and radius of a circle for the given equation using two ways. Firstly using general formula, secondly using standard formula by completing square method.

a) $x^{2}+y^{2}+2y= 5$

b) $x^{2}+4x +y^{2}+6y= 3$

Identify the graphs of the following equations as a circle, a point or an empty set.

a) $x^{2}+y^{2}+2y= 5$

b) $x^{2}+4x +y^{2}+6y+13=0$

c) $x^{2}+10x +y^{2}+2y+36=0$

Equation of circle (standard form)

August 12, 2023/by admin_ct

Equation of a circle in standard form.

Equation of a circle which is centered at origin (0,0), with radius r, is given in standard form as:

$\dpi{120} x^{2}+y^{2}=r^{2}$

Above equation can also be obtained using distance formula between points (0,0) and (x,y) . Distance between these two points is ‘r’

Equation of a circle in center-radius form is given as:

Equation of a circle with center (h,k) and radius r is written in standard form as:

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

Lets work on some problems based on circle:

Write the equation of a circle with center (-1,2) and radius as 5.

Here we have center (h,k) as (-1,2) and radius r= 5.

Now plugin these values into standard center -radius form of circle.

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

$\dpi{120} \left ( x- -1 \right )^{2}+\left ( y-2 \right )^{2}=5^{2}$

$\dpi{120} \left ( x+1 \right )^{2}+\left ( y-2 \right )^{2}=25$

To get the general form of circle, we just need to expand the squares

$\dpi{120} x^{2}+2x+1 +y^{2}-4y+4 =25$

$\dpi{120} x^{2}+2x +y^{2}-4y+5 =25$

How do you find the equation of a circle with center at the origin and passing through (-2, -3)?

Since the circle is centered at origin so we have center (h,k) as (0,0).

Now plugin given point (-2,-3) as (x,y) and (0,0) as center (h,k) into standard form.

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

$\dpi{120} \left ( -2-0 \right )^{2}+\left ( -3-0 \right )^{2}=r^{2}$

$\dpi{120} \left ( -2 \right )^{2}+\left ( -3 \right )^{2}=r^{2}$

$\dpi{120} 4+9=r^{2}$

$\dpi{120} 13=r^{2}$

Finally , we can write circle equation as,

$\dpi{120} x^{2}+y^{2}= 13$

State the coordinates of center and measure of radius for the circle whose equation is given as ${\color{Red} \left ( x-2 \right )^{2}+\left ( y+3 \right )^{2}=9}$

Rewriting the given equation as , $\left ( x-2 \right )^{2}+\left ( y--3 \right )^{2}=9$

Comparing the given circle equation with standard form $\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

we get h = 2

k = -3

and $r^{2}=9$

$r=\pm \sqrt{9}$

r = 3 , as radius measure can’t be negative so we drop negative sign and get r= 3

Therefore, the center of given circle is (2,-3) and radius = 3

Find equation of a circle with the diameter that has end points at (0,1) and (2,5).

We know that mid point of diameter is the center of circle. So first we find center of circle using mid point formula.

$(h,k) = \left ( \frac{x_{1}+x{_{2}}}{2},\frac{y_{1}+y_{2}}{2} \right )$

$(h,k) = \left ( \frac{0+2}{2},\frac{1+5}{2} \right )$

$(h,k) = (1,3)$

Next step is to find radius which can be found two ways,

firstly, using distance formula on end points of diameter and making it half and

secondly , using distance formula on center and any end point of diameter.

Since second way is shorter so lets use this way.

Using distance formula on center (1,3) and end point (0,1) which is easier to use out of these two end points.

$D=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$

$D=\sqrt{(1-0)^{2}+(3-1)^{2}}$

$D=\sqrt{(1)^{2}+(2)^{2}}$

$D=\sqrt{1+4}= \sqrt{5}$

Since distance D is the radius r, we can plugin coordinates of center (h,k) and radius r into standard form

$\dpi{120} \left ( x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$

$\dpi{120} \left ( x-1 \right )^{2}+\left ( y-3 \right )^{2}=(\sqrt{5})^{2}$

$\dpi{120} \left ( x-1 \right )^{2}+\left ( y-3 \right )^{2}=5$

Two boats leave the same dock

August 7, 2023/by admin_ct

Two boats leave the same dock at the same time, one travelling due west at 9 miles per hour and the other due north at 15 miles per hour. How many miles apart are the boats after three hours?

Solution: To get the answer of this question , it would be better to sketch it first. Use the fact that 4 directions are perpendicular to each other.

Step 1 : Find distances travelled by boats using the given rates. These distances are the two legs of right triangle.

Distance = speed * time

First leg = 15 *3 = 45 miles

Second leg= 9*3= 27 miles

Using Pythagorean for this right triangle, we find the longest side.

$H^{2}=(45)^{2}+(27)^{2}$

$H^{2}=2754$

$H=\sqrt{2754}$

H= 52.4785… ≈ 52.48 miles

After 3 hours , boats are 52.48 miles apart.

Inscribed Angle problems

August 5, 2023/by admin_ct

Inscribed angle

An inscribed angle has a vertex on a circle and sides (arms) which are the chords of circle.

An intercepted arc has end points on the sides of an inscribed angle and lies in the interior of inscribed angle.

In the above figure ∠QRS is the inscribed angle and arc QS is the intercepted arc.

Inscribed Angle theorem:

If an angle is inscribed in a circle, then the measure of angle equals one half the measure of intercepted arc.

$\angle QRS = \frac{1}{2} \times m \widehat{QS}$

Here are some problems on inscribed angle theorem:

In the figure below ΔABC is inscribed in the circle. Find the measure of arc AC.

Solution:

Here ∠ABC is the inscribed angle and arc AC is the intercepted arc.

That means to find arc AC, we need to find ∠ABC first.

∠ABC + 80+45 = 180 [ using triangle’s angle sum property ]

∠ABC = 180-125

∠ABC = 55

$\angle ABC = \frac{1}{2} \times m \widehat{AC}$ [ Using inscribed angle theorem ]

$55 = \frac{1}{2} \times m \widehat{AC}$

$2\times 55 = m \widehat{AC}$

$110 = m \widehat{AC}$

Therefore measure of arc AC is 110º.

In the figure below, points A, B, C and D are on the circle. The measure of arc AB is 65 and measure of arc BC is 70 . Find measure of angle ADC.

Solution: We know that

$\angle ADB = \frac{1}{2} \times m \widehat{AB}$ [ using inscribed angle theorem ]

$\angle ADB = \frac{1}{2} \times 65 = 32.5$

Similarly,

$\angle BDC = \frac{1}{2} \times m \widehat{BC}$

$\angle BDC = \frac{1}{2} \times 70 = 35$

$\angle ADC= \angle ADB +\angle BDC$

$\angle ADC= 32.5 +35 = 67.5$

Theorem : The angle at the centre is twice the angle at the circumference subtended by the same arc.

In the figure given below find angle FHG.

Solution: We know that the angle at the centre is twice the angle at the circumference subtended by the same arc. Therefore to find angle FHG we need to first find angle at the center intercepted by arc GF.

$\angle HEG +\angle HEF + \angle FEG = 360$ [ complete angle around a point is 360 ]

$153 + 125 + \angle FEG = 360$

$\angle FEG = 360-278 = 82$

∠FEG at the center would be twice of ∠FHG at the circumference as they both are subtended by same arc GF.

$\angle FEG = 2\angle FHG$

$82 = 2\angle FHG$

$41 = \angle FHG$

$\angle FHG=41^{\circ}$

Theorem : If two inscribed angles of a circle intercept the same arc , then the angles are congruent.

In the following figure , find angle D and C

Solution: Since angle D and C both are intercepted by same arc TS , so their measures would be equal.

3x-5=2x+15

3x-2x=15+5

x= 20

Angle D = 3x-5 = 3(20)-5 = 55

Angle C = 2x+15 = 2(20)+15 = 55

Therefore measure of each angle C and D is 55.

Thales Theorem

July 31, 2023/by admin_ct

This is a special case of inscribed angle theorem, an important theorem of circle geometry. This theorem can be stated in any of the following ways:

If three points A, B, and C lie on the circumference of a circle, where the line AC is the diameter of the circle, then the angle ∠ABC is a right angle (90°)

The diameter of a circle always subtends a right angle to any point on the circle.

An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle.

Here is an interesting and very easy proof of Thales theorem:

To prove this we use following two facts:

– Sum of all angles of a triangle is 180.

– Base angles of an isosceles triangle are equal.

In this circle we have :

$\overline{OA}=\overline{OB}=\overline{OC}$ reason being all are radii of same circle.

$\angle OAB=\angle OBA =\alpha$ reason being base angles of isosceles triangle OAB

Similarly ,

$\angle OBC=\angle OCB =\beta$ reason being base angles of isosceles triangle OBC

Also, $\angle ABC=\alpha +\beta$

Since sum of all angles of a triangle is 180 , so

$\angle ABC+\angle BCA +\angle CAB = 180$

$(\alpha +\beta )+\beta +\alpha = 180$

$2(\alpha +\beta )= 180$

$(\alpha +\beta )= 90$

$\therefore \angle ABC= 90^{\circ}$

Here are some examples on Thales Theorem:

1. In the given circle FH is a diameter passing through its center J. Find x and angle HFG.

Since FH is a diameter so using Thales theorem, FGH would be a right triangle with right angle at point G.

Therefore we can apply triangle’s angle sum property,

$\angle HFG +\angle FGH +\angle FHG = 180$

$4x+2 +90 +9x-3 = 180$

$4x+9x+2-3+90 = 180$

$13x+89 = 180$

$13x = 91$

$x = 7$

$\therefore \angle HFG = 4x+2 = 4(7)+2= 30$

$\angle HFG = 30^{\circ}$

2. In the given circle, find the measure of angle PQR . Assume point R is the center of the circle.

Since R is given center of circle, PS would be the diameter of the circle.

Therefore applying Thales theorem for triangle PQS, angle PQS would be a right angle.

$\angle PQS=90$

Since RS = RQ (radii of same circle) , base angles of isosceles triangle RQS would be equal.

$\angle RQS=\angle RSQ = 24$

Also

$\angle PQS = \angle PQR +\angle RQS$

$90 = \angle PQR + 24$

$66 = \angle PQR$

Hence the measure of angle PQR = 66

3. In the circle shown, BC is a diameter with center A. Given m∠ABE = 26 and m∠ADB=18

Find a) m∠DAB b) m∠BAE c) m∠DAE

Since A is the center of circle, so AB=AD=AE , as all are radii of same circle.

Therefore ABD is an isosceles triangle and hence base angles would be equal.

$\angle ADB=\angle ABD = 18$

Using triangle’s angle sum property,

$\angle ABD +\angle ADB +\angle DAB = 180$

$18+18 +\angle DAB = 180$

$\angle DAB = 180-(18+18)$

$\angle DAB = 144^{\circ}$

b) Using exactly same concept for triangle ABE, we have

$\angle AEB=\angle ABE = 26$

Using triangle’s angle sum property,

$\angle ABE +\angle AEB +\angle BAE = 180$

$26+26 +\angle BAE = 180$

$\angle BAE = 180-(26+26)$

$\angle BAE = 128^{\circ}$

c) We see that three angles make a complete angle of 360 at point A.

$\angle DAB +\angle BAE +\angle DAE = 360$

$144 +128 +\angle DAE = 360$

$\angle DAE = 360-(144 +128)$

$\angle DAE = 88^{\circ}$

4. In the figure below, O is the center of circle and AD is a diameter.

a. Find 𝑚∠𝐴OB.
b. If 𝑚∠BOC ∶ 𝑚∠𝐶OD = 6:5 , what is 𝑚∠𝐵OC?

Since OB = OD being radii of same circle,

$\therefore \angle OBD = \angle ODB$ as base angles of isoscele triangles are equal.

$\therefore \angle OBD = \angle ODB=24$

Using exterior angle property of triangles, exterior angle is equal to sum of opposite interior angles.

$\therefore ext\angle AOB = 24+24= 48$

$\angle BOD = 180-48= 132$

$\angle BOD= \angle BOC+\angle COD$

These two angles are given in the ratio 6 : 5

$\therefore 6x+5x= 132$

11x= 132

x= 12

$\angle BOC = 6x = 6*12 = 72$

$\angle BOC = 72^{\circ}$

In the given circle, suppose arcRQT = 106 and m

July 28, 2023/by admin_ct

In the given circle, suppose ${\color{Red} m\widehat{RQT}=106^{\circ}}$ and ${\color{Red} m\angle QRS = 73^{\circ}}$ Find the following.

Solution:

We know that,

Measure of inscribed angle = 1/2 × measure of intercepted arc

$\therefore \angle RST = \frac{1}{2}\times \widehat{RQT}$

$\therefore \angle RST = \frac{1}{2}\times 106 = 53^{\circ}$

Now look at the definition of cyclic quadrilateral.

A cyclic quadrilateral is a four sided shape that can be inscribed into a circle. Each vertex of the quadrilateral lies on the circumference of the circle and is connected by four chords.

Therefore given quadrilateral STQR is a cyclic quadrilateral.

And using the property of cyclic quadrilateral ‘The opposite angles of a cyclic quadrilateral have a total of $180°.$ $180° ‘$

we can easily find the remaining two angles.

$\angle RST +\angle RQT =180$

$53 +\angle RQT =180$

$\angle RQT =180-53=127^{\circ}$

Similarly

$\angle QTS =180-73=107^{\circ}$

$\mathbf{m\angle RQT =127^{\circ}}$

$\mathbf{m\angle QTS =107^{\circ}}$

Circles: Central angle, Chords and Arcs

July 25, 2023/by admin_ct

In the given circle , QS is a diameter. Suppose $\dpi{120} {\color{Red} m \widehat{QR}= 44^{\circ}}$ and $\dpi{120} {\color{Red} m\angle QRT = 57^{\circ}}$ . Find the following.

Solution: We know that,

Measure of inscribed angle = 1/2 × measure of intercepted arc

$\therefore \angle QSR = \frac{1}{2}\times \widehat{QR}$

$\angle QSR = \frac{1}{2}\times 44= 22^{\circ}$

Also $\angle QRT = \frac{1}{2}\times \widehat{QT}$

$57 = \frac{1}{2}\times \widehat{QT}$

$\widehat{QT}= 57\times 2=114^{\circ}$

Since QS is given diameter of the circle , Therefore arc QTS is a semicircle measuring 180.

$\widehat{ST}=\widehat{QTS}-\widehat{QT}$

$\widehat{ST}=180-114=66$

Again using Inscribed angle and intercepted arc theorem, we can find angle $\angle SRT=\frac{1}{2}\times \widehat{ST}$

$\angle SRT=\frac{1}{2}\times66 =33^{\circ}$

$\angle SRQ=57+33=90^{\circ}$

Using angle sum property of triangles, we know that sum of all angles of a triangle is 180

So we can easilt find third missing angle.

$\angle RQS=180-(22+90)=68^{\circ}$

$\mathbf{\angle SRT = 33^{\circ}}$

$\mathbf{\angle RQS = 68^{\circ}}$

Finding expressions for sine and cosine graphs.

July 25, 2023/by admin_ct

Determine the formula for cosine function graphed below.

Solution: First we write general equation of cosine function.

$Y = A cos(B(x-D))+C$

First we draw a mid line ( dashed line) passing horizontally through the middle of this graph and follow the procedure given below.

look at the distance of max or min point of this graph from this midline. This will give you amplitude A= 4
Look at the distance of mid line (dashed one) from x axis. This gives you vertical shift C =4
Look at the period which is the distance between either two consecutive max points or two min points. Then use formula $B=\frac{2\pi }{period}$
Here distance between two max points (period) = 7-1= 6.
$B=\frac{2\pi }{6} = \frac{\pi }{3}$
Phase shift is the horz shift. Here graph is shifted to right horizontally by 1 unit so D=1
Finally plugin all the values of A,B,C and D into general cosine fucntion and we get
$Y = 4 cos(\frac{\pi }{3}(x-1))+4$

Solved worksheets for AP calculus

August 29, 2020/by admin_ct

Homogeneous Differential Equations

January 16, 2020/by admin_ct

What is homogeneous differential equation?

If a first order, first degree differential equation is expressible in the form

$\dpi{120} \mathbf{\frac{dy}{dx}=\frac{f(x,y)}{g(x,y)}}$

where f(x,y) and g(x,y) are homogeneous functions of the same degree, then it is called a homogeneous differential equation.

Such type of equations can be reduced to variable separable form by some suitable substitution like y=vx.

What is homogeneous function?

A function f(x,y) is called a homogeneous function of degree n if

$\dpi{120} \mathbf{f(\lambda x,\lambda y)=\lambda ^{n}f(x,y)}$

For example ,

$\dpi{120} f(x,y)=x^{2}-y^{2}+5xy$

is a homogeneous function of degree 2 because

$\dpi{120} f(\lambda x,\lambda y)=\lambda ^{2}x^{2}-\lambda ^{2}y^{2}+5\lambda x\lambda y=\lambda ^{2}f(x,y)$

Example1: Solve the differential equation (x+y)dy+(x-y)dx=0 given that y=1 when x=1.

Solution: (x+y)dy+(x-y)dx=0

$\frac{dy}{dx}=\frac{y-x}{x+y}$

Here both numerator y-x and denominator x+y are functions of degree 1 , therefore this is homogeneous differential equation.

Using substitution, y=vx

$\frac{dy}{dx}=v+x\frac{dv}{dx}$

Original DE get changed to,

$v+x\frac{dv}{dx}=\frac{vx-x}{x+vx}$

Dividing numerator and denominator with x and subtracting v we get,

$x\frac{dv}{dx}=\frac{v-1}{1+v}-v$

$x\frac{dv}{dx}=\frac{v-1-v^{2}-v}{1+v}$

$x\frac{dv}{dx}=\frac{-(v^{2}+1)}{1+v}$

$\frac{v+1}{v^{2}+1}dv =\frac{-dx}{x}$

$\int \frac{v+1}{v^{2}+1}dv =\int \frac{-dx}{x}$

$\int \frac{v}{v^{2}+1}dv +\int \frac{1}{v^{2}+1}dv=-\int \frac{dx}{x}$

$\frac{1}{2}\int \frac{2v}{v^{2}+1}dv +\int \frac{1}{v^{2}+1}dv=-\int \frac{dx}{x}$

$\frac{1}{2}ln(v^{2}+1)+tan^{-1}(v)=-ln|x|+C$

$ln(v^{2}+1)+2ln|x|+2tan^{-1}(v)=2C$

$ln(v^{2}+1)+lnx^{2}+2tan^{-1}(v)=2C$

$ln[(v^{2}+1)x^{2}]+2tan^{-1}(v)=2C$

Plugin back v as y/x, we get expression as

$ln[(\frac{y^{2}}{x^{2}}+1)x^{2}]+2tan^{-1}(\frac{y}{x})= K where K=2C$

$ln(y^{2}+x^{2})+2tan^{-1}(\frac{y}{x})= K$

Using given condition that y=1 when x=1 we get,

$ln(1+1)+2tan^{-1}(1)= K$

$ln(2)+2(\frac{\pi }{4})= K$

$ln(2)+\frac{\pi }{2}= K$

Using value of constant K we get the solution as,

$ln(y^{2}+x^{2})+2tan^{-1}(\frac{y}{x})= ln(2)+\frac{\pi }{2}$

Example2: Solve the following differential equation.

${\color{Red} (4 x^{4}+x^{3}y+y^{4})dx-x^{4}dy=0}$

Solution:

$(4 x^{4}+x^{3}y+y^{4})dx=x^{4}dy$

$\frac{dy}{dx}=\frac{(4 x^{4}+x^{3}y+y^{4})}{x^{4}}$

Substitute y=vx and we get the above equation transformed as,

$v+x\frac{dv}{dx}=\frac{(4 x^{4}+x^{4}v+v^{4}x^{4})}{x^{4}}$

$v+x\frac{dv}{dx}= 4+v+v^{4}$

$x\frac{dv}{dx}= 4+v^{4}$

$\frac{dv}{4+v^{4}}= \frac{dx}{x}$

$\int \frac{dv}{4+v^{4}}= \int \frac{dx}{x}$

$\int \frac{dv}{2^{2}+(v^{2})^{2}}= \int \frac{dx}{x}$

$\frac{1}{2}tan^{-1}\left ( \frac{v^{2}}{2} \right )=ln|x|+C$

Plugin back v=y/x

$\frac{1}{2}tan^{-1}\left ( \frac{y^{2}}{2x^{2}} \right )=ln|x|+C$

Example3: Solve the following homogeneous differential equation

${\color{Red} xsin\left ( \frac{y}{x} \right )\frac{dy}{dx}=ysin\left ( \frac{y}{x} \right )+x}$

Solution:

$\frac{dy}{dx}=\frac{ysin\left ( \frac{y}{x} \right )+x}{ x sin\left ( \frac{y}{x} \right )}$

Substitute y=vx and we get the above equation transformed as,

$v+x\frac{dv}{dx}=\frac{(vx) sin\left ( \frac{vx}{x} \right )+x}{ x sin\left ( \frac{vx}{x} \right )}$

$v+x\frac{dv}{dx}=\frac{(vx) sin\left ( v\right )+x}{ x sin\left (v \right )}$

$v+x\frac{dv}{dx}=\frac{ x(v sin\left ( v\right )+1)}{ x sin\left (v \right )}$

$v+x\frac{dv}{dx}=\frac{ v sin\left ( v\right )+1}{ sin\left (v \right )}$

$x\frac{dv}{dx}=\frac{ v sin\left ( v\right )+1}{ sin\left (v \right )}-v$

$x\frac{dv}{dx}=\frac{ v sin\left ( v\right )+1-vsin(v)}{ sin\left (v \right )}$

$x\frac{dv}{dx}=\frac{ 1}{ sin\left (v \right )}$

$sin(v)dv= \frac{dx}{x}$

$\int sin(v)dv= \int \frac{dx}{x}$

-cos(v) = ln|x|+C

cos(y/x)=-ln|x|-C

Sometimes a homogeneous differential equation is expressible in the form,

$\dpi{120} \frac{dx}{dy}=\frac{f(x,y)}{g(x,y)}$

In such a situation, we substitute x=vy and proceed same way .

Example4: Solve

$\dpi{120} {\color{Red} 2ye^{\frac{x}{y}}dx +(y-2xe^{\frac{x}{y}})dy=0}$

Solution:

$\frac{dx}{dy}=\frac{2xe\frac{x}{y}-y}{2ye^{\frac{x}{y}}}$

Let x=vy, then

$\frac{dx}{dy}=v+y\frac{dv}{dy}$

And the given DE can be rewritten as,

$v+y\frac{dv}{dy}=\frac{2vye^{v}-y}{2ye^{v}}$

$y\frac{dv}{dy}=\frac{2ve^{v}-1}{2e^{v}}-v$

$y\frac{dv}{dy}=\frac{2ve^{v}-1-2ve^{v}}{2e^{v}}$

$y\frac{dv}{dy}=\frac{-1}{2e^{v}}$

$2e^{v}dv=-\frac{1}{y}dy$

$\int 2e^{v}dv=-\int \frac{1}{y}dy$

$2e^{v}=- \ln (y)+lnC$

$2e^{\frac{x}{y}}=ln|\frac{c}{y}|$

Practice problems:

Solve the following homogeneous differential equations.

1. $2xy\frac{dy}{dx}=x^{2}+y^{2}$

2. $xyln\left (\frac{x}{y} \right )dx+\left ( y^{2}-x^{2} ln\left ( \frac{x}{y} \right )\right )dy=0$

3. $xdy-ydx=\sqrt{x^{2}+y^{2}}dx$

Solve the following initial value problem

4. $x(x^{2}+3y^{2})dx+y(y^{2}+3x^{2})dy=0 ;y(1)=1$

Answers:

1. $x=c(x^{2}-y^{2})$

2. $\frac{x^{2}}{y^{2}}\left ( ln\left ( \frac{x}{y}\right )-\frac{1}{2} \right )+lny^{2}=c$

3. ${y+\sqrt{x^{2}+y^{2}}}= cx^{2}$

4. $x^{4}+6x^{2}y^{2}+y^{4}=8$

Archives

x2 + y2 + 2gx + 2fy + c = 0.

Practice problems:

Equation of a circle in standard form.

Theorem : The angle at the centre is twice the angle at the circumference subtended by the same arc.

Theorem : If two inscribed angles of a circle intercept the same arc , then the angles are congruent.

In the given circle , QS is a diameter. Suppose and . Find the following.

What is homogeneous differential equation?

What is homogeneous function?

x² + y² + 2gx + 2fy + c = 0.

In the given circle , QS is a diameter. Suppose $\dpi{120} {\color{Red} m \widehat{QR}= 44^{\circ}}$ and $\dpi{120} {\color{Red} m\angle QRT = 57^{\circ}}$ . Find the following.