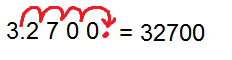1. If f(x)=|x-3| then f'(1) is
a) 0
b) 1
c) -1
d) Non existent
Solution: Derivative of this absolute function can be found either by using definition of absolute value function or by using formula.
Lets first use definition of absolute value function.
&space;=\begin{cases}&space;&&space;x-3&space;\text{&space;if&space;}&space;x\geq&space;3&space;\\&space;&&space;-(x-3)&space;\text{&space;if&space;}&space;x&space;<&space;3&space;\end{cases})
Since x=1 lie in second domain (x<3) so we use lower function.
f(x) = -(x-3)
f ‘(x) = -(1-0) =-1
Therefore f ‘(1) = -1. Option c is correct.
Other way: Using formula for derivative of absolute functions.
Let f(x) = |U| where U= g(x)
Then =\frac{U}{|U|}*U') or
or =\frac{g(x)}{|g'(x)|}*g'(x))
=\frac{(x-3)}{|x-3|}*(x-3)')
=\frac{(1-3)}{|1-3|}*1&space;=\frac{-2}{|-2|}&space;=\frac{-2}{2}=-1)
2. Given that &space;=x^{10}h(x)}) and h(-1)=4 , h'(-1) = 7 . Then find f ‘(-1).
and h(-1)=4 , h'(-1) = 7 . Then find f ‘(-1).
a) 4
b) -33
c)-40
d)-70
Solution: Since f(x) is a product of two functions x^10 and h(x) so we use product rule to find derivative f'(x)
=(x^{10})'h(x)+x^{10}h'(x))
=(10x^{9})'h(x)+x^{10}h'(x))
=10(-1)^{9}h(-1)+(-1)^{10}h'(-1))
Plugin given values of h(1) and h'(-1)
=&space;-10(4)+&space;(1)(7))
f ‘(-1) = -33
Option b) -33 is correct answer.
3. If &space;=\frac{(x+2)^2)(x^2&space;-1)}{3}}) and
and =&space;f(\sqrt{x+1})}) what is the value of g'(3) ?
what is the value of g'(3) ?
a) 16
b) 1/4
c) 4
d) 16
Solution : First we find derivative of g(x) using chain rule.
=&space;f'(\sqrt{x+1})*&space;(\sqrt{x+1})')
=&space;f'(\sqrt{x+1})*&space;\frac{1}{2\sqrt{x+1}})
=&space;f'(\sqrt{3+1})*&space;\frac{1}{2\sqrt{3+1}})
=&space;f'(2)*&space;\frac{1}{2*2})
To get f'(2) we plugin x=2 into given expression for f'(x)
&space;=\frac{(2+2)^2(2^2&space;-1)}{3}=&space;16)
Using f'(2)= 16 we get g'(3) as
g'(3) = 16 *(1/4) = 4
g'(3)= 4
So option c is the answer.
4. Functions f, g and h are twice differentiable functions with g(2)= h(2)= 4. The line }) is tangent to both the graphs of g at x=2 and graph of h at x=2.
is tangent to both the graphs of g at x=2 and graph of h at x=2.
a) find h'(2)
b) Let a be a function given as
=&space;3x^3&space;h(x)}) . Write an expression for a'(x) and a'(2).
. Write an expression for a'(x) and a'(2).
c) The function h satisfies that =&space;\frac{x^2-4}{1-(f(x))^3}&space;;&space;x&space;\neq&space;2}) . It is known that
. It is known that }) can be evaluated using L Hospital’s rule. Use this limit to find f(2) and f ‘(2).
can be evaluated using L Hospital’s rule. Use this limit to find f(2) and f ‘(2).
d) It is known that g(x) ≤ h(x) for 1<x<3. Let k be a function satisfying g(x)≤k(x)≤h(x) for 1<x<3. Is k continuous at x=2? Justify your answer.
Solution: It is known that slope of tangent line to the curve at given point is same the slope of curve at that point.
Slope of tangent line at x=2 is 2/3
and that would be the slope of curve h(x) at x=2. so h'(2) = 2/3.
b) =&space;3x^3&space;h(x)) . Since given function is product of two functions so using product rule,
. Since given function is product of two functions so using product rule,
![a'(x)= 3[(x^3)' h(x) + x^3 h'(x)]](https://latex.codecogs.com/gif.latex?a'(x)=&space;3[(x^3)'&space;h(x)&space;+&space;x^3&space;h'(x)])
![a'(x)= 3[(3x^2)' h(x) + x^3 h'(x)]](https://latex.codecogs.com/gif.latex?a'(x)=&space;3[(3x^2)'&space;h(x)&space;+&space;x^3&space;h'(x)])
![a'(2)= 3[(3(2)^2)' h(2) + 2^3 h'(2)]](https://latex.codecogs.com/gif.latex?a'(2)=&space;3[(3(2)^2)'&space;h(2)&space;+&space;2^3&space;h'(2)])
![a'(2)= 3[12*4 + 8*2/3]](https://latex.codecogs.com/gif.latex?a'(2)=&space;3[12*4&space;+&space;8*2/3])
a'(2) = 160
c)
=&space;\lim_{x\rightarrow&space;2}&space;\frac{x^2-4}{1-(f(x))^3})
It is given that this limit can be evaluated using L Hospital’s rule. Which means it would have intermediate form(0/0) when x approaches to 2. so we have
)^3}&space;=&space;\frac{0}{0})
)^3=0)
)^3=&space;1&space;\Rightarrow&space;f(2)=&space;1)
Since h(x) is continuous so we have,
=h(2))
Using L Hospital’s rule to find its limit,
=&space;\lim_{x\rightarrow&space;2}&space;\frac{(x^2-4)'}{(1-(f(x))^3)'}&space;=&space;\frac{2x-0}{0-3(f(x))^2&space;f'(x)}) = 4
= 4
)^2&space;f'(x)}&space;=4)
)^2&space;f'(2)}&space;=4)
^2&space;f'(2)}&space;=4)
}&space;=1)
)
d) Given that
\leq&space;k(x)\leq&space;h(x)&space;on&space;1<x<3)
Since g(x) and h(x) are given continuous and g(2)= h(2) = 4
&space;=4) and
and &space;=4) . Using sandwich theorem we can conclude that,
. Using sandwich theorem we can conclude that,
&space;=4) and k(2)= 4
and k(2)= 4
Therefore K(x) is continuous at x=2.
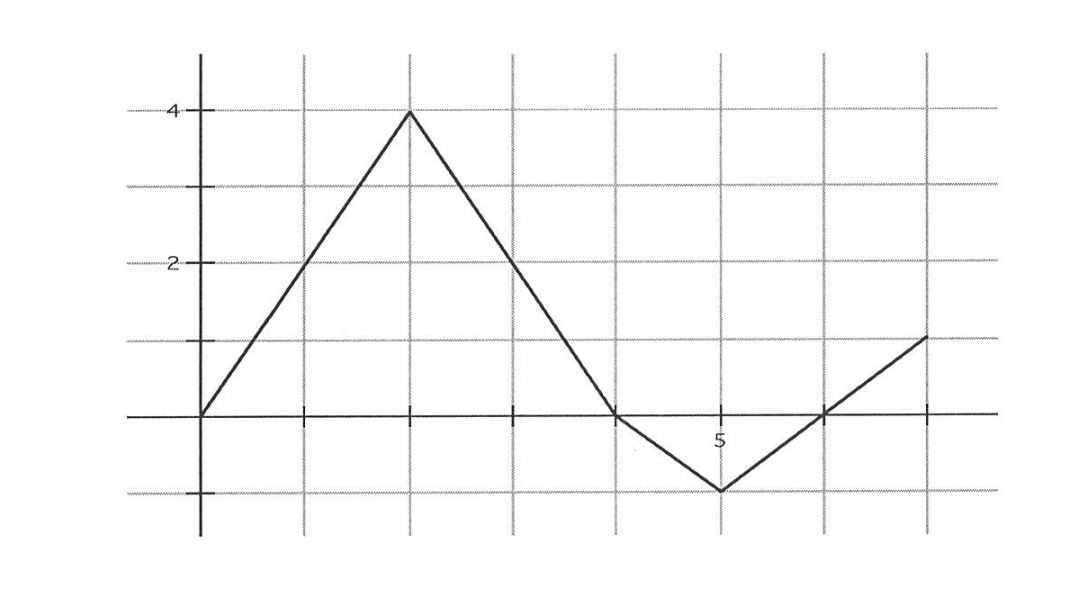
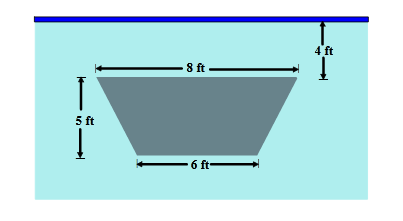
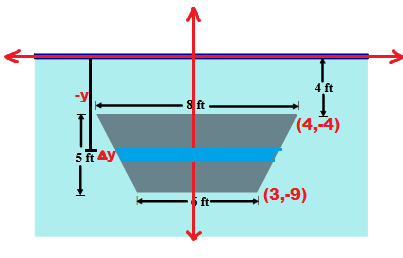
5. Let =&space;\int_{2}^{x}f(t)&space;dt}) for 0≤t≤7 where the graph of differentiable function f, is shown below.
for 0≤t≤7 where the graph of differentiable function f, is shown below.
a) Find g(3) , g'(3) and g”(3)
Using the given definition of g(x) we have,
=&space;\int_{2}^{3}f(t)&space;dt) which means the area under the curve f(t) from x=2 to x=3. This area can be found using geometric formulas.
which means the area under the curve f(t) from x=2 to x=3. This area can be found using geometric formulas.
Area under the curve for given x values is a trapezoid, so we can use trapezoid’s area formula.
A = 1/2 (sum of parallel sides)* distance between parallel sides.
g(3) = A= 1/2(2+4)*1 = 6/2 = 3
Using Fundamental Theorem of Calculus
g'(3) = f(3) = 2
And g”(3)= f ‘(3) which is slope of tangent line at x=3
slope = (4-0)/(2-4) = -2
so g”(3) = -2
b) Find average rate of change of g(x) on 0≤c≤3
Average rate = -g(0)}{3-0})
For that first we need to find g(0) , same way as we had found g(3).
=&space;\int_{2}^{0}f(t)&space;dt)
Which can be rewritten using property of definite integral.
=&space;-\int_{0}^{2}f(t)&space;dt) . which represent the area under the curve from 0 to 2.
. which represent the area under the curve from 0 to 2.
g(0) = – [(1/2)*2*4] = -4
Average rate = -g(0)}{3-0}&space;=&space;\frac{3-(-4)}{3}&space;=&space;\frac{7}{3})
c) For how many values of c, where 0<c<3, is g'(c) equal to average rate found in part b? Justify your answer.
We know that ,
=&space;\int_{2}^{c}f(t)&space;dt)
then g'(c) = f(c) = 7/3
And the function f(t) gets the value 7/3 twice on the interval 0<c<3.
d) Find the Graph of gx coordinate of each point of inflection of the graph of g on the interval 0<t<7. Justify your answer.
We know that g'(x) = f(x) and g”(x)= f'(x).
Graph of g will have inflection points where f(x) changes its direction. We can observe from given graph of f that it changes direction from increasing to decreasing at x=2 and again from decreasing to increasing at x=5. Also slopes f ”(2) and f”(5) are undefined being sharp corners. So the two inflections points are at x=2,5.
6. For what values of a and c , is the piecewise function differentiable.
=\begin{cases}&space;&&space;ax^2+sinx,&space;\text{&space;if&space;}&space;x\leq&space;\pi&space;\\&space;&&space;2x-c&space;,&space;\text{&space;if&space;}&space;x&space;>&space;\pi&space;\end{cases}&space;})
We know that functions 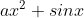 and 2x-c are continuous and differentiable in their respective domains.
and 2x-c are continuous and differentiable in their respective domains.
=\begin{cases}&space;&&space;2ax+cosx,&space;\text{&space;if&space;}&space;x\leq&space;\pi&space;\\&space;&&space;2&space;,&space;\text{&space;if&space;}&space;x&space;>&space;\pi&space;\end{cases})
We are given that piecewise function is differentiable at x=π too. That means left and right hand derivatives of given function would be same at x=π. Therefore,
=\begin{cases}&space;&&space;2a&space;\pi&space;+cos(\pi&space;)&space;,&space;\text{&space;if&space;}&space;x\leq&space;\pi&space;\\&space;&&space;2&space;,&space;\text{&space;if&space;}&space;x&space;>&space;\pi&space;\end{cases})
2aπ +cos(π) = 2
2aπ -1 = 2
2a π = 3
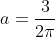
Also piecewise function is continuous at pi so left and right hand limits would be same as f(π)
Left limit is,
=&space;a\pi&space;^2+sin(\pi&space;)=&space;a\pi&space;^2) which is same as value of function , i.e f(π)
which is same as value of function , i.e f(π)
And right limit is ,
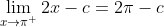
For the function to be continuous. we set left and right limits equal ,
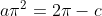

Plugin value of a = 3/2π , we get
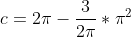
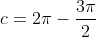
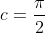
So the solution is
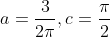
7. When the height of a cylinder is 12 cm and the radius is 4cm, the circumference of the cylinder is increasing at a rate of  cm/min, and the height of the cylinder is increasing four times faster than the radius. How fast is the volume of the cylinder changing?
cm/min, and the height of the cylinder is increasing four times faster than the radius. How fast is the volume of the cylinder changing?
Given: height of cylinder(h)= 12 cm
radius of cylinder(r) = 4 cm
Rate of increase of circumference (2πr)
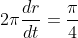
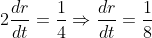
Height of cylinder is increasing 4 times faster than rate of change of radius.
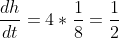
To find : Rate of change of volume 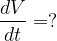
Volume of cylinder is given as,
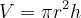
Differentiating both sides using product rule, with respect to time(t) ,
)
Plugin value into this expression.
\frac{1}{8}*12+4^2*\frac{1}{2}&space;\right&space;))
&space;=&space;20\pi)
So the volume of cylinder is changing at the rate of 20π cubic cm/min.
8. Let f be a function that is differentiable on open interval (1,10), If, f(1) = -6 ,f(5)= 2 , and f(10) = -4. Which of the following must be true. Justify your answer.
i. f has atleast two zeros.
ii. The graph of f has atleast one horizontal tangent.
iii. f ‘(5) =0
iv. For some c, 1<c<10 , f(c) =1
v. For some c, 1<c<10 , f ‘(c)= 2/9
i, ii, iv and v must be true. Here is the reason for each.
i. f has atleast two zeros.
When we move from left to right on interval (1,10) , y values goes from negative to positive (-6 to 2 ) and then again from positive to negative (from 2 to -4) that means function’s graph will cross x axis atleast twice. Which proves f has atleast two zeros.
ii. Since function’s graph cross x axis twice so graph will turn atleast once and there is horizontal tangent at each turn. This proves there is atleast one turn and hence atleast one horizontal tangent.
iv. Since the given function is differentiable and hence continuous. This graph is going from -6 to 2 when x is changing from 1 to 5 , that means continuous graph will pass through y value 1, while going from -6 to 2. So there must be some x value c on given interval such that f(c)=1
v. Since function is given differentiable and hence continuous on interval (1,10) , it satisfy hypothesis of Mean Value Theorem. That means there exist a number c on interval (1,10) which satisfy conclusion of MVT.
Therefoere,
=\frac{f(10)-f(1)}{10-1})
=\frac{-4+6}{9}=&space;\frac{2}{9})
which proves the statement “ For some c, 1<c<10 , f ‘(c)= 2/9″
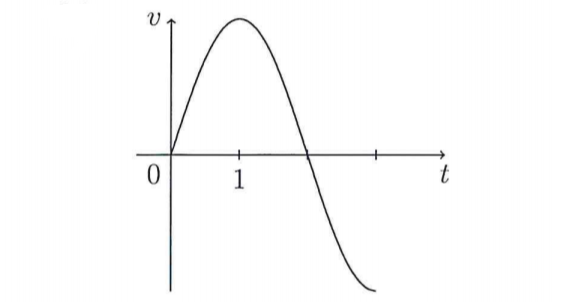
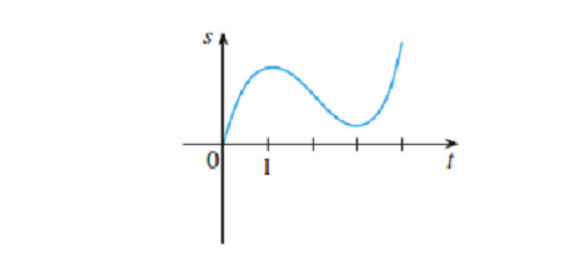
9. Graph of velocity function of a particle is shown below, where t is measured in seconds. Find the intervals when particle is speeding up and slowing down.
First we observe the given graph. We see that particle start at t=0 , reach max velocity at t=1 .
We make the following observations by looking at the graph :-
Acceleration is positive as long as velocity graph is increasing and acceleration is negative as long as velocity graph is decreasing because acceleration is nothing but the slope of velocity.
Velocity is positive as long as graph is above x axis and velocity is negative as long as graph is below x axis.
Velocity is 0 at t=0 and t=2 seconds. It reaches to max value at t=1. So we make the following chart.
0<t<1
- Velocity (V)
- Acceleration (A)
Rules to follow :
Particle is speeding up when velocity and acceleration both have same signs. Particle is slowing down when they have opposite signs.
So the answer is :
Particle is speeding up on intervals : (0,1) and (2,3)
slowing down on interval : (1,2)
10 . A particle moves according to position function =&space;\frac{t}{1+t^2}}) on the interval t ≥0 where t is measured in seconds and S in feet.
on the interval t ≥0 where t is measured in seconds and S in feet.
a) Find when particle is at rest.
Particle is at rest when its velocity is 0. So we find velocity function by taking its derivative and then set velocity function =0 and solve for t.
=S'(t)=&space;\frac{(1+t^2)t'&space;-&space;t(1+t^2)'}{(1+t^2)^2})
=&space;\frac{(1+t^2)1&space;-&space;t(2t)}{(1+t^2)^2}&space;=\frac{1+t^2&space;-2t^2}{(1+t^2)^2})
&space;=\frac{1-t^2}{(1+t^2)^2})
&space;=0&space;\Rightarrow&space;\frac{1-t^2}{(1+t^2)^2}=0)
This expression would be 0 when its numerator is 0 so,
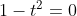
t = -1,1
But t=-1 doesn’t lie in the given domain so we accept only t=1.
That means particle is at rest at t=1 second
b) Find the intervals for which particle is moving in positive(right) and negative(left) directions.
Particle is moving towards right when velocity is positive and moving towards left when velocity is negative. So we need to check the intervals where velocity is positive and where it is negative. Domain is given [0,∞) which is divided into two intervals by t=1 (when velocity is 0) So we get the two intervals as,
[0,1) and (1,∞)
For interval [0,1) We get V(0.5) > 0
Velocity is positive, that means particle is moving towards right on [0,1)
For interval (1,∞) , We get V(2) < 0
Velocity is negative, that means particle is moving towards left on (1,∞)
c) Find the total distance traveled in first 8 seconds.
To find total distance, we find distance traveled in positive direction as well as in negative direction.
Distance traveled in positive direction:
-S(0)&space;\right&space;|=&space;\frac{1}{2}&space;-0&space;=&space;\frac{1}{2}) ft.
ft.
Distance traveled in negative direction:
-S(1)&space;\right&space;|=&space;\frac{1}{2}&space;-\frac{8}{65})
Total Distance :
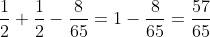 ft
ft
d) When the particle is speeding up and slowing down?
To find when the particle is speeding up or slowing down, we need to find acceleration function. We know that acceleration is derivative of velocity function. so,
=&space;V'(t)=\frac{(1+t^2)^2(1-t^2)'-((1+t^2)^2)'(1-t^2)}{(1+t^2)^4})
=&space;\frac{(1+t^2)^2(-2t)-2(1+t^2)(2t)(1-t^2)}{(1+t^2)^4})
![a(t)= \frac{(1+t^2)[(-2t)(1+t^2)-2(2t)(1-t^2)]}{(1+t^2)^4}](https://latex.codecogs.com/gif.latex?a(t)=&space;\frac{(1+t^2)[(-2t)(1+t^2)-2(2t)(1-t^2)]}{(1+t^2)^4})
![a(t)= \frac{[(-2t)(1+t^2)-2(2t)(1-t^2)]}{(1+t^2)^3}=\frac{-2t-2t^3-4t+4t^3}{(1+t^2)^3}](https://latex.codecogs.com/gif.latex?a(t)=&space;\frac{[(-2t)(1+t^2)-2(2t)(1-t^2)]}{(1+t^2)^3}=\frac{-2t-2t^3-4t+4t^3}{(1+t^2)^3})
=&space;\frac{-6t+2t^3}{(1+t^2)^3}=\frac{2t(t^2-3)}{(1+t)^3})
Setting a(t)=0 and solving for t, we get
=0)
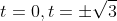
But -√3 doesn’t lie in the given domain, so we have only t=0 and t=√3 .
Using t=√3 , we get the domain t≥0 divided into two intervals as [0,√3) and (√3,∞). Now we check each interval one by one.
For interval [0,√3) we get ,
=\frac{2*1(1^2-3)}{(1+1)^3}&space;=&space;\frac{-1}{2}&space;<&space;0)
Acceleration is negative during this interval.
For interval (√3,∞)
=\frac{2*2(2^2-3)}{(1+2)^3}&space;=&space;\frac{4}{27}&space;>&space;0)
Acceleration is positive during this interval.
Lets make a sign chart using velocity and acceleration results,
0<t<1
- Velocity (v)
- Acceleration(a)
Using the fact that particle will be speeding up when both velocity and acceleration have same signs (either both positive or both negative) and speeding down when both have different signs, we get the following results.
Speeding up on 1<t<√3
Speeding down on 0<t<1 and t>√3.
Practice Worksheet
- Find derivative of given function:
=&space;2sin^{-1}(4x^3))
- Find second derivative of
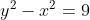
- Find x values of the horizontal tangents of the curve
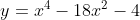
- Given the function
=&space;ax-bx^2) . Determine the values of a and b such that the line 3y-6x+6=0 is tangent to the function at x=3.
. Determine the values of a and b such that the line 3y-6x+6=0 is tangent to the function at x=3.
- At time t, the position of a body moving along the x-axis is given as
=&space;t^3&space;-21t^2&space;+144t) . Find the body’s acceleration
. Find the body’s acceleration
each time the velocity is zero.
- The graphs of f and g are shown below. Use them to evaluate
a) '(5)) b)
b) }{f(x)}&space;\right&space;)_{x=5})
7. A particle moves along a coordinate axis in the positive direction to the right. Its position at time  is given by
is given by  . Find
. Find  and
and  and use these values to answer the following questions.
and use these values to answer the following questions.
a) Is the particle moving from left to right or from right to left at time  ?
?
b) Is the particle speeding up or slowing down at time
8. The velocity-time graph of an object moving along a straight line is shown below. Find the intervals for which object is slowing down.
9. Find least value of a such that the function =&space;x^2+ax+1) is increasing on [1,2].
is increasing on [1,2].
10. A man is walking at the rate of 6.5 km/hr towards the foot of a tower 120 m high. At what rate is he approaching the top of tower when he is 50m away from tower?
Answers:
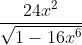
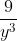
- x=-3, 0, 3
- a= 2/3 , b=-2/9
- a(6)= -6m/s^2 and a(8)=6m/s^2
- a) 1/6 b)7/24
- a) Right to left b) slowing down
- (1,3)
- -2
- 2.5 km/hr
to standard notation.
=
to standard form.
=
to standard form.
so the given number remain same without any change in it.