How to do partial fraction decomposition.
Any proper rational function }{g(x)}) can be expressed as a sum of rational functions. Each such fraction is called partial fraction and the process of obtaining them is called decomposition of into partial fractions.
can be expressed as a sum of rational functions. Each such fraction is called partial fraction and the process of obtaining them is called decomposition of into partial fractions.
The decomposition of }{g(x)}) into partial fractions mainly depand upon the nature of factors of g(x).
into partial fractions mainly depand upon the nature of factors of g(x).
Case 1:
When denominator g(x) is expressible as the product of non – repeating linear factors (x-a1)(x-a2)….(x-an) then rational function }{g(x)}) is decomposed as..
is decomposed as..
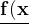}{g(x)}=&space;\frac{A_{1}}{(x-a_{1})}+\frac{A_{2}}{(x-a_{2})}+......+\frac{A_{n}}{(x-a_{n})}})
Where A1, A2,……An are constants and can be determined by equating the numerators on left side and right side and then substituting x=a1 , a2,…….. an
Example1:Resolve 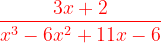 into partial fractions.
into partial fractions.
Solution: First we get factors of denominator as (x-1)(x-)(x-3). Since all are non repeated linear factors, so expression get decomposed like this:
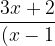(x-2)(x-3)}=\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{x-3})
Multiply each term on both sides with (x-1)(x-2)(x-3) and we get, (This is short way of doing common denominators)
(3x+2) = A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(x-2)
Values of constants A,B and C can be obtained by two ways.
First method: by substituting zeros of denominator as x values. Here zeros are 1,2 and 3 so we plugin x=1,2 and 3 one by one.
Let x=1 ,
(3*1+2) = A(1-2)(1-3)+B(1-1)(1-3)+C(1-1)(1-2)
5 = A(-1)(-2) +B(0)(-2) +C(0)(-1)
5 = 2A
5/2 = A
Let x=2 ,
(3*2+2) = 0 +B(2-1)(2-3) +0
8 = -B
-8 = B
Let x= 3,
(3*3+2) = 0+0+C(3-1)(3-2)
11 = 2C
11/2 = C
Using values of A,B and C given expression can be decomposed as,
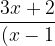(x-2)(x-3)}=\frac{5}{2(x-1)}-\frac{8}{x-2}+\frac{11}{2(x-3)})
Second method:By comparing coefficients of like terms. After getting rid of denominators on both sides, we multiply and simplify the terms on right side like this..
(3x+2)= A(x-2)(x-3) +B(x-1)(x-3) +c(x-1)(x-2)
(3x+2) = A(x^2 -5x+6 )+B(x^2 -4x+3 )+C(x^2-3x+2 )
(3x+2) =x^2 (A+B+C) + x(-5A-4B-3C)+ 6A+3B+2C
Comparing coefficients of like terms we get following three linear equations.
0=A+B+C 3=-5A-4B-3C 2=6A+3B+2C
Solving these three linear equations by substitution or elimination we get A=5/2 ,B=-8 and C=11/2
For non repeated linear factors ,first method is always helpful while second method is helpful for all other types.
Case 2:
When denominator is expressible as the product of linear factors such that some of them are repeating.
=(x-a)^{k}(x-a_{1})(x-a_{2}))
then,
![\dpi{120} \mathbf{\frac{f(x)}{g(x)}= \left [\frac{A_{1}}{(x-a)}+\frac{A_{2}}{(x-a)}+......+\frac{A_{k}}{(x-a)^{k}} \right ]+\frac{B_{1}}{(x-a_{1})}+\frac{B_{2}}{(x-a_{2})}}](https://latex.codecogs.com/gif.latex?\dpi{120}&space;\mathbf{\frac{f(x)}{g(x)}=&space;\left&space;[\frac{A_{1}}{(x-a)}+\frac{A_{2}}{(x-a)}+......+\frac{A_{k}}{(x-a)^{k}}&space;\right&space;]+\frac{B_{1}}{(x-a_{1})}+\frac{B_{2}}{(x-a_{2})}})
[for repeated linear factors] [non repeated]
Example2:Resolve the given expression into partial fractions and then evaluate the integral.
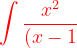^{3}(x+1)}dx})
Solution:
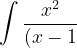^{3}(x+1)}dx=&space;\frac{A}{(x-1)}+\frac{B}{(x-1)^{2}}+\frac{C}{(x-1)^{3}}+\frac{D}{(x+1)})
Multiply both sides with ^{3}(x+1)) we get,
we get,
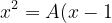^{2}(x+1)+B(x-1)(x+1)+C(x+1)+D(x-1)^{3})
Let x=1
1= A(0)(1)+B(0)(1)+C(1+1)+D(0)
1= 2C
½ = C
Let x=-1
(-1)^2= A(1)(0)+B(-2)(0)+C(0)+D
1 = -8D
-1/8 = D
Let x=0
0 =A(1)(1)+B(-1)(1)+C(1)+D(-1)
0 = A-B+C-D ———-(i)
Let x = 2
4 = 3A+3B+3C+D ——–(ii)
Plugin C=1/2 and D=-1/8 in equations (i) and (ii) we get,
A-B =-5/8 and A+B=7/8
Solving these two equations using elimination we get,
A = 1/8 , B= 3/4
Using values of A,B,C and D we get the expression decomposed as,
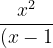^{3}(x+1)}=&space;\frac{1}{8(x-1)}+\frac{3}{4(x-1)^{2}}+\frac{1}{2(x-1)^{3}}-\frac{1}{8(x+1)})
And the integral becomes ,
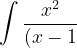^{3}(x+1)}dx=&space;\frac{1}{8}\int&space;\frac{1}{(x-1)}dx+\frac{3}{4}\int&space;\frac{1}{(x-1)^{2}}dx+\frac{1}{2}\int&space;\frac{1}{(x-1)^{3}}dx)
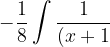}dx)
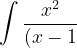^{3}(x+1)}dx=&space;\frac{1}{8}ln|x-1|+\frac{3}{4}\frac{(x-1)^{-1}}{-1}+\frac{1}{2}\frac{(x-1)^{-2}}{-2})
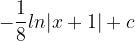
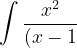^{3}(x+1)}dx=&space;\frac{1}{8}ln|x-1|-\frac{1}{8}ln|x+1|-\frac{3}{4(x-1)}-\frac{1}{4(x-1)^{2}}+c)
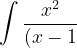^{3}(x+1)}dx=&space;\frac{1}{8}ln&space;\left&space;|\frac{x-1}{x+1}&space;\right&space;|&space;-\frac{3}{4(x-1)}-\frac{1}{4(x-1)^{2}}+c)
Case 3:
When some factors are quadratic along with some linear factors. Then for each linear factor we use numerator as constant alone and for each quadratic factor we use numerator as linear function of the form Ax+B.
Lets work on a similar example to understand this case .
Example3: Resolve the given expression into partial fractions.
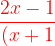(x^{2}+2)}dx})
Solution:
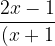(x^{2}+2)}dx=\frac{A}{(x+1)}+\frac{Bx+C}{x^{2}+2})
Multiply both sides with (x+1)(x^2+2)
(2x-1) = A(x^2 +2) +(Bx+C)(x+1)
(2x-1) = Ax^2 +2A+Bx^2 +(B+C)x + C
2x-1= (A+B)x^2 +(B+C)x +2A+C
Comparing coefficients of like terms,
0=A+B 2=B+C -1=2A+C
-A=B 2=-A+C -1=2A+C
Solving equations 2=-A+C and -1=2A+C together by subtracting
We get, A=-1
Using A=-1 we get B=-(-1)= 1
Using A=-1 we get C=2+A=2-1=1
Using A=-1 ,B=1 ,C=1 we get the given expression resolved as,
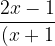(x^{2}+2)}dx=\frac{-1}{(x+1)}+\frac{x+1}{x^{2}+2})
Important: If a rational function contains only even powers of x in both numerator and denominator , then x^2 can be replaced with some other variable (say t) and proceed same way using linear factors.
Example4 : Resolve into partial fractions and then integrate the given expression.
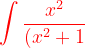(x^{2}+4)}dx})
Solution: Since top and bottom functions both have even powers of x so we assume x^2= t
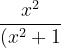(x^{2}+4)}&space;=\frac{t}{(t+1)(t+4)}=\frac{A}{t+1}+\frac{B}{t+4})
t = A(t+4) + B(t+1)
plugin t=-1, we get
-1 = A(-1+4) +B(0)
-1=3A
-1/3 = A
Plugin t=-4, we get
-4= A(0) +B(-3)
4/3 =B
Using values of A and B we get the expression decomposed as..
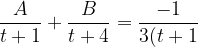}+\frac{4}{3(t+4)}=\frac{-1}{3(x^{2}+1)}+\frac{4}{3(x^{2}+4)})
Taking integral,
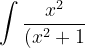(x^{2}+4)}dx&space;=\int&space;\frac{-1}{3(x^{2}+1)}dx+\int&space;\frac{4}{3(x^{2}+4)}dx)
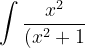(x^{2}+4)}dx&space;=\frac{-1}{3}\int&space;\frac{1}{(x^{2}+1)}dx+\frac{4}{3}\int&space;\frac{1}{(x^{2}+4)}dx)
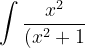(x^{2}+4)}dx&space;=\frac{-1}{3}tan^{-1}(x)+\frac{4}{3}*\frac{1}{2}tan^{-1}(\frac{x}{2})+c)
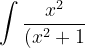(x^{2}+4)}dx&space;=\frac{-1}{3}tan^{-1}(x)+\frac{2}{3}tan^{-1}(\frac{x}{2})+c)
Case 4:
When factors are quadratic and repeating.
Following example illustrates the procedure.
Example5: Resolve the given expression into partial fractions.
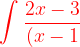(x^{2}+1)^{2}}dx})
Solution:
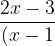(x^{2}+1)^{2}}=\frac{A}{x-1}+\frac{Bx+c}{(x^{2}+1)}+\frac{Dx+E}{(x^{2}+1)^{2}})
Multiplying both sides with (x-1) we get,
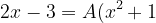^{2}+(Bx+C)(x-1)(x^{2}+1)+(Dx+E)(x-1))
Plugin x=1 we get,
-1 = A(1+1)^2
-1 = 4A
-1/4 =A
Comparing coefficients of like terms we get,
A+B=0 C-B=0 2A+B-C+D=0 C+E-B-D=2 A-C-E=-3
Substitute A=-1/4 and solving these equations, we get
B=C=1/4 D=1/2 and E= 5/2
Using values of A,B,C,D and E we get the given expression decomposed as,
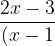(x^{2}+1)^{2}}=\frac{\frac{-1}{4}}{x-1}+\frac{\frac{1}{4}(x+1)}{(x^{2}+1)}+\frac{\frac{1}{2}x+\frac{5}{2}}{(x^{2}+1)^{2}})
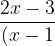(x^{2}+1)^{2}}=\frac{-1}{4(x-1)}+\frac{(x+1)}{4(x^{2}+1)}+\frac{x+5}{2(x^{2}+1)^{2}})
Here is an useful summary chart on partial decomposition rules.
| Type of factors
In denominator |
Expression |
Form of partial fractions |
| Linear factors
Repeated linear factors
Irreducible Quadratic factors
Repeated quadratic factors
|
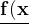}{(x+a)(x+b)}})
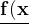}{(x+a)^{k}}})
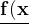}{(x+a)(ax^{2}+bx+c)}})
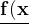}{(ax^{2}+bx+c)^{k}}})
|
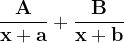
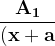}+\frac{A_{2}}{(x+a)^{2}}+.......+\frac{A_{n}}{(x+a)^{k}}})
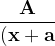}+\frac{Bx+C}{(ax^{2}+bx+c)}})
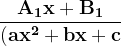}+\frac{A_{2}x+B_{2}}{(ax^{2}+bx+c)^{2}}+....+\frac{A_{k}x+B_{k}}{(ax^{2}+bx+c)^{k}}})
+ |
Practice problems:
Resolve the following expressions into partial fractions.
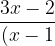^{2}(x+1)(x+2)})
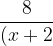(x^{2}+4)})
Evaluate the following integrals using partial fractions.
3. 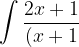(x-2)}dx)
4.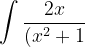(x^{2}+3)}dx)
Answers:
1. 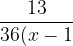}+\frac{1}{6(x-1)^{2}}-\frac{5}{4(x+1)}+\frac{8}{9(x+2)})
2. 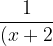}+\frac{-x+2}{x^{2}+4})
3. 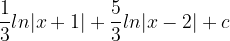
4. 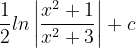
is positive and we assume a positive series ∑
for comparison .This test says:
[dividing both numerator and denominator with 3^n]
(which is a finite value)
(a finite value)
being a harmonic series , is always divergent,