Topic Archive - Page 5 of 7 - Celestial Tutors

Law of Cosines and its Applications

September 6, 2019/by admin_ct

Law of Cosines and its Applications

Law of Cosines is used to solve triangles in the following two cases.

Three sides (SSS)
Two sides and included angle (SAS)

because in these cases none of the ratios in law of Sines would be complete.

Example1. Using law of Cosines, solve the triangle with given sides a=10 , b=12 , c=16. Round your answers to two decimal places.

Solution: Using alternative form of law of Cosines,

$\dpi{120} cosA=\frac{b^{2}+c^{2}-a^{2}}{2bc}$

Plug in values of a, b and c

$\dpi{120} cosA=\frac{12^{2}+16^{2}-10^{2}}{2*12*16}= 0.78125$

$\dpi{120} A= cos^{-1}(0.78125)= 38.62^{\circ}$

$\dpi{120} cosB=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{10^{2}+16^{2}-12^{2}}{2*10*16}=0.6625$

$\dpi{120} B= cos^{-1}(0.6625)= 48.51^{\circ}$

To find third angle we can use angle sum property of triangles.

C = 180-(38.62+48.51) =92.87°

Example2. Determine whether the Law of Sines or the Law of Cosines is needed to solve the triangle. Then solve the triangle.

a=8, c=5, B=40

Solution: Given two sides and included angle so we use law of Cosines.

$\dpi{120} b^{2}=a^{2}+c^{2}-2accosB$

$\dpi{120} b^{2}=8^{2}+5^{2}-2*8*5cos(40)$

b^2 = 27.71644

b = 5.26

Next we can use law of Sines to find Angle A or C.

$\dpi{120} \frac{sinB}{b}=\frac{sinC}{c}$

$\dpi{120} \frac{sin40}{5.26}=\frac{sinC}{5}$

$\dpi{120} \frac{sin40}{5.26}*5=sinC$

$\dpi{120} sin^{-1}(0.6110)= C$

37.66° =C

To find angle A, we can use angle sum property of triangle

A= 180-(40+37.66) =102.34°

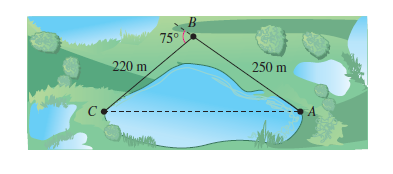
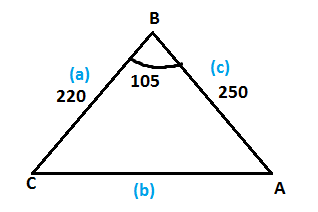
Example3. To approximate the length of a marsh, a surveyor walks 250 meters from point A to point B, then turns 75° and walks 220 meters to point C as shown in figure. Approximate the length AC of the marsh.

Solution: Here we know that < B =180-75=105 and we get the following equivalent geometric figure.

We need to find length AC which is side b, using law of Cosines,

$\dpi{120} b^{2}=a^{2}+c^{2}-2accosB$

$\dpi{120} b^{2}=220^{2}+250^{2}-2*220*250cos(105)$

b^2 = 139370.09496

b = 373.32 miles

So the length of marsh is 373.32 miles.

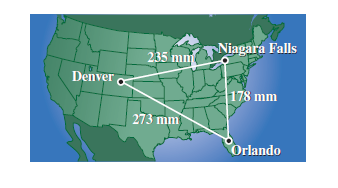
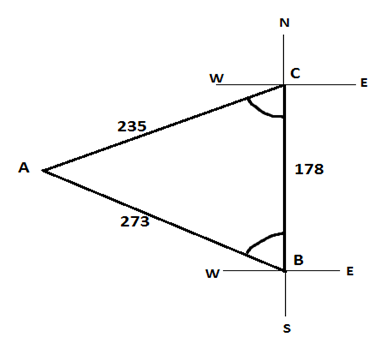
Example4. On a map, Orlando is 178 millimeters due south of Niagara Falls, Denver is 273 millimeters from Orlando, and Denver is 235 millimeters from Niagara Falls (see figure).

(a) Find the bearing of Denver from Orlando.

(b) Find the bearing of Denver from Niagara Falls.

Solution:

Here we need to find angle B and C for parts a and b respectively. So using law of Cosines,

$\dpi{120} cosB=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{178^{2}+273^{2}-235^{2}}{2*178*273}=0.524632$

$\dpi{120} B= cos^{-1}(0.524632)= 58.4^{\circ}$

Bearing of Denver is towards west of Orlando which is in north so it is written as

B = N58.4° W

$\dpi{120} cosC=\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{178^{2}+235^{2}-273^{2}}{2*178*235}=0.147979$

$\dpi{120} C= cos^{-1}(0.147979)= 81.5^{\circ}$

Bearing of Denver is towards west of Niagara which is in south so it is written as

C = S81.5° W

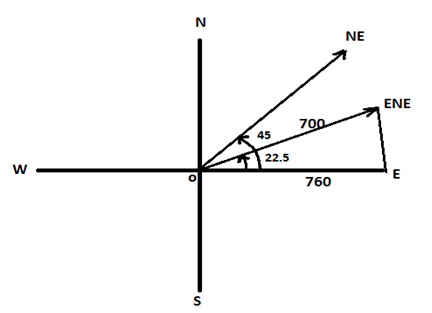
Example5. Two airplanes flying together in formation take off in different directions. One flies due east at 350 mph, and the other flies east-northeast at 380 mph. How far apart are the two airplanes 2 hr after they separate, assuming that they fly at the same altitude?

Solution: Following diagram will help to understand the given situation. Airplane 1 is moving along the track OE and airplane 2 is moving along track OENE. Angle between east and east northeast is always 22.5°

In 2 hrs. airplane 1 will travel the distance =350*2= 700 miles

In 2 hrs. airplane 2 will travel the distance =380*2= 760 miles

So we have sides as 700 and 760 and included angle as 22.5.

Using law of cosines,

$\dpi{120} b^{2}=a^{2}+c^{2}-2accosB$

$\dpi{120} b^{2}=700^{2}+760^{2}-2*700*760cos(22.5)$

b = 290.84 miles

So the two airplanes are 290.84 miles apart after 2 hours.

Practice problems:

Use law of Cosines to solve the following triangles .

a) A=120° , b= 6 , c=7

b) a=8, b=19, c=14

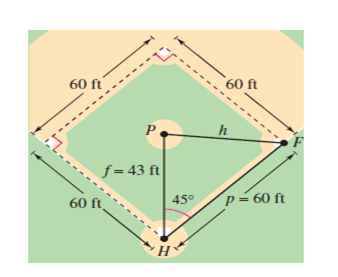
The pitcher’s mound on a women’s softball field is 43 feet from home plate and the distance between the bases is 60 feet, as shown in figure. (The pitcher’s mound is not halfway between home plate and second base.) How far is the pitcher’s mound from first base?

Answers:

a) B=27.46° , C=32.54° , a=11.27

b)A=22.08° , B=116.80° , C=41.12°

2. 42.43 ft.

Ferris Wheel problems (applications of trigonometric functions)

September 5, 2019/by admin_ct

Ferris Wheel (applications of trigonometric functions)

One of the most common applications of trigonometric functions is, Ferris wheel, since the up and down motion of a rider follows the shape of sine or cosine graph.

Equations used :

Y = aSin(bx-c)+d or

Y = aCos(bx-c)+d

Formula used :

Amplitude, $\dpi{120} \mathbf{a=\frac{\left | max-min \right |}{2}}$

$\dpi{120} \mathbf{b=\frac{2\pi }{period}}$ vertical shift d=(max+min)/2

Example1. A Ferris wheel has a diameter of 30 m with its center 18 m above the ground. It makes one complete rotation every 60 seconds. Assuming rider starts at the lowest point, find the trigonometric function for this situation and graph the function.

Solution:

Amplitude – radius of the wheel makes the amplitude so amplitude(a) = 30/2 =15.

Period– Wheel complete one rotation in 60 seconds so period is 60 sec. Using period we can find b value as,

$\dpi{120} b=\frac{2\pi }{p}=\frac{2\pi }{60}=\frac{\pi }{30}$

Phase shift– There is no phase shift for this cosine function so no c value.

Vertical shift– Centre of wheel is 18m above the ground which makes the mid line, so d= 18.

Lowest point would be 18-15=3m and highest point would be 18+15= 33m above the ground. So the rider will start from 3m and reach to a height of 33 m in half the period (30 sec) and come back to lowest point (3m) again in 60 secs. So its graph would look like this.

As the graph start from lowest point and the pattern is upside down so we put a negative sign in front of cos. Summing up all the parameters above we get trigonometric function as,

$\dpi{120} Y=-15cos\left ( \frac{\pi }{30}t \right )+18$

Example2. A water wheel on a paddle boat has a radius of 2 m. The wheel rotates every 30 secs and bottom 0.6m of wheel is submerged in water.

Considering the water surface as x axis , determine the cosine equation of the graph starting from a point at the top of wheel.
Graph the height of a point on the wheel relative to the surface of water, starting from highest point.
How long is the point on wheel under water.

Solution: a)

Radius of wheel gives the amplitude so a= 2

Period =30 secs , so

$\dpi{120} b=\frac{2\pi }{p}=\frac{2\pi }{30}=\frac{\pi }{15}$

Since radius is 2 and bottom point is -0.6, mid line will be at 2-0.6 =1.4m

Combining all the above parameters and considering top point as starting point , we get the cosine equation as,

$\dpi{120} Y=2cos\left ( \frac{\pi }{15}t \right )+1.4$

c) To find the time for wheel under water we need to find x intercepts , intersection of cosine function with y=0(water surface) using graphic calculator. We get the intersection points as x=11.2s and x=18.8s So the total time for wheel underwater is 18.8-11.2 = 6 seconds.

Example3. The earliest sunset occurs at 5:34 PM on Dec. 21 and latest at 11:45 PM on June 21.

Write cosine equation of the graph.
Draw the graph approximating the sunrise time during the year.
What is the sunset time on April 6.
The sunset time is earlier than 8PM for what percentage of the year.

Solution:

First of all we need to convert time from hour/min to decimal hour form. 5PM is equal to 17 hours and 34 min. are equal to 34/60=0.57 so we get 5:34PM equal to 17.57 hrs.

Same way we get 11:45PM equal to 23.75 hrs. because 11PM is equal to 12+11=23hrs and 45 min = 45/60 =0.75hrs.

Using these maximum and minimum values we get amplitude

$\dpi{120} a=\frac{\left | 23.75-17.57 \right |}{2}= 3.1$

For these type of problems, period is taken as 365 days. so,

$\dpi{120} b=\frac{2\pi }{p}=\frac{2\pi }{365}$
Starting the graph on Jan1, max. value occurs on 21 June so

c = 31+28+31+30+31+21=172 days

Central line would be

d = (23.75+17.57)/2 = 20.66

Combining all above parameters , we get cosine function as,

$\dpi{120} Y= 3.1 cos\left [ \frac{2\pi }{365}(x-172) \right ]+20.66$

This equation can also be written as,

$\dpi{120} Y= -3.1 cos\left [ \frac{2\pi }{365}(x+10) \right ]+20.66$ considering 21 Dec. as lowest point.

3) To find sunset time on April6, we find what day of year it is.

31+28+31+6 = 96

So we plug in x as 96 into the equation found in part a.

$\dpi{120} Y= 3.1 cos\left [ \frac{2\pi }{365}(96-172) \right ]+20.66 =21.46$

Converting back 21.46 into decimal hour form we get,

21-12=9 and .46*60= 28 min

So sunset time on April 6 is 9:28PM.

4) Sunset is earlier than 8PM for days 0 to 68 and then again days 276 to 365. So that total number of days are 157 which are 43 % of the year.

Example 4: The following table gives the average recorded monthly temperature throughout the year.

Write the cosine equation for the graph corresponding to the table given above.

Solution:

Amplitude, a = [22-(-17)]/2 =39/2 = 19.5

Period = 12 months, here months are used instead of days.

$\dpi{120} b=\frac{2\pi }{p}=\frac{2\pi }{12}=\frac{\pi }{6}$

Since the maximum temp. occur in the month of July which is the 7^th month so there is a phase shift of 7.

c = 7

Vertical shift d =[22+(-17)]/2 = 5/2 =2.5

Combining all the parameters above, we get the final equation as,

$\dpi{120} Y= 19.5 cos\left [ \frac{\pi }{6}(x-7) \right ]+2.5$

Where x represents number of months and y represents approximate temperature.

Practice problems:

1) A Ferris wheel with radius 40 ft complete one revolution every 60 seconds. The lowest point of wheel is 5 m above the ground.

Draw the graph of the situation, starting with a person getting on the bottom of the wheel at t=0 seconds.
Determine an equation representing the path of the person on Ferris wheel.
Determine how high the person will be after riding for 40 seconds.
When the person first reach 50 ft.

2) The bottom of a windmill is 8m above the ground, and the top is 22m above the ground. The wheel rotates once every 5 seconds.

Determine the cosine equation of the graph.
Draw the graph of two complete cycles.

3)The average temp. for Regina is hottest at 27 on July 28, and coolest at -16 on January 10.

Draw the graph and write the cosine equation for the graph.
The average temp. is higher than 23 for how many days.

4)The latest sunrise occurs at 9:10 AM on Dec 21. The earliest occurs at 3:43 AM on June 21. Write the cosine equation for the graph.

Answers:

1. $\dpi{120} Y=-40cos\left ( \frac{\pi }{30}x \right )+45$ , 65 ft , 16.2s
2. $\dpi{120} Y=-7cos\left ( \frac{2\pi }{5}x \right )+15$
3. $\dpi{120} Y=21.5 cos\left ( \frac{2\pi }{365}(x-209) \right )+ 5.5 , 72 days$
4. $\dpi{120} Y=-2.73cos\left ( \frac{2\pi }{365}(x-172) \right )+6.45$

Evaluating Trigonometric functions

September 5, 2019/by admin_ct

Evaluating Trigonometric functions

In this lesson we work on finding values of different trigonometric functions using various identities and formulas.

We can use sum and difference formulas, half angle and double angle formulas to evaluate the values of different trigonometric functions.

Example: Find the exact value of cos(π/12).

Solution: Here we use the fact that $\dpi{120} \frac{\pi }{12}=\frac{\pi }{3}-\frac{\pi }{4}$

Then using the formula cos(x-y) = cosx cosy + sinx siny

$\dpi{120} cos\frac{\pi }{12}=cos\left (\frac{\pi }{3}-\frac{\pi }{4} \right )$

= cos(π/3 ) cos( π/4) + sin(π/3) sin(π/4 )

$\dpi{120} =\frac{1}{2}*\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{2}$

$\dpi{120} = \frac{\sqrt{2}+\sqrt{6}}{4}$

Example: Find the exact value of sin(17π/12 ).

Solution: Here we use the fact that $\dpi{120} \frac{17\pi }{12}=\frac{9\pi }{4}-\frac{5\pi }{6}$

Then using the formula sin(x-y) = sinx cosy – cosx siny

$\dpi{120} sin\frac{17\pi }{12}=sin\left (\frac{9\pi }{4}-\frac{5\pi }{6} \right )$

sin(17π/12) = sin(9π/4)cos(5π/6) – cos(9π/4 )sin( 5π/6) ———(i)

Now we find exact values of sin(9π/4) , cos(5π/6) ,cos(9π/4) , sin(5π/6 ) using equivalent acute angles.

$\dpi{120} sin\left (\frac{9\pi }{4} \right )=sin\left ( 2\pi +\frac{\pi }{4} \right )=sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}$

$\dpi{120} cos\left (\frac{9\pi }{4} \right )=cos\left ( 2\pi +\frac{\pi }{4} \right )=cos\frac{\pi }{4}=\frac{\sqrt{2}}{2}$

$\dpi{120} sin\left (\frac{5\pi }{6} \right )=sin\left ( \pi -\frac{\pi }{6} \right )=sin\frac{\pi }{6}=\frac{1}{2}$

$\dpi{120} cos\left (\frac{5\pi }{6} \right )=cos\left ( \pi -\frac{\pi }{6} \right )=-cos\frac{\pi }{6}=-\frac{\sqrt{3}}{2}$

Plugin all these values into —(i) we get,

$\dpi{120} sin\left ( \frac{17\pi }{12} \right )=\frac{\sqrt{2}}{2}*\frac{-\sqrt{3}}{2}-\frac{\sqrt{2}}{2}*\frac{1}{2}=\frac{-\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{-\sqrt{6}-\sqrt{2}}{4}$

Example: Find the exact value of sin(u+v) given that sinu=5/13 and cosv = -3/5 (Both u and v are in quadrant II)

Solution: To find value of sin(u+v) we need to get values of sinv and cosu first, which can be found either by using Pythagorean identities or using right triangle. We also need to take care of signs used with sinv and cosu using ASTC rule.

$\dpi{120} cosu=\sqrt{1-sin^{2}u}= \sqrt{1-\left ( \frac{5}{13} \right )^{2}}= \sqrt{\frac{144}{169}}=\frac{12}{13}$

Since u is given in 2^nd quadrant so cosu would be negative .

Cosu = -12/13

$\dpi{120} sinv=\sqrt{1-cos^{2}v}= \sqrt{1-\left ( \frac{-3}{5} \right )^{2}}= \sqrt{\frac{16}{25}}=\frac{4}{5}$ [ sinv is positive being in 2^nd quadrant]

Now we can substitute the values of sinu, cosu, sinv and cosv into the following formula.

Sin(u+v) = sinu cosv +cosu sinv

$\dpi{120} =\frac{5}{13}*\frac{-3}{5}+\frac{-12}{13}*\frac{4}{5}$

$\dpi{120} =\frac{-15}{65}+\frac{-48}{65}=\frac{-63}{65}$

Example: Write the following trigonometric expression as an algebraic expression.

Sin(arcsin x+arcos x)

Solution: First we assume this given function as sin(u+v)

Sin(u+v) = sinu cosv + cosu sinv

Where u=arc sin x v=arc cosx

$\dpi{120} u=sin^{-1}x$ $\dpi{120} v= cos^{-1}x$

sinu =x cosv =x

Here we can use right triangles to find values of cosu and sinv.

$\dpi{120} cosu=\frac{\sqrt{1-x^{2}}}{1}$ $\dpi{120} sinv=\frac{\sqrt{1-x^{2}}}{1}$

Sin(arcsin x+arcos x) = sin(u+v) =sinu cosv + cosu sinv

$\dpi{120} =x*x+\frac{\sqrt{1-x^{2}}}{1}*\frac{\sqrt{1-x^{2}}}{1}$

$\dpi{120} =x^{2}+1-x^{2}=1$

Example: prove the identity. $\dpi{120} {\color{Red} cos\left ( \pi -\theta \right )+sin\left ( \frac{\pi }{2}+\theta \right )=0}$

Solution: Using identities cos(x-y) and sin(x+y) we get,

cos( π)cosθ + sin(π )sin(θ) +sin(π/2)cosθ +cos(π/2)sin(θ)=0

We know that cos(π) = -1 sin(π) = 0

cos(π/2) = 0 sin(π/2 ) = 1

Substituting these values we get,

(-1) cosθ + (0)sin( θ) + (1)cosθ +(0)sin(θ) = 0

-cos(θ) +0 +cos(θ) +0 = 0

-cos(θ ) + cos( θ) = 0

0 = 0

Example: Find exact value of the expression.

Sin 75 + sin15

Solution: To solve this, we make use of sum to product formula

$\dpi{120} sinx+siny=2sin\left ( \frac{x+y}{2} \right )cos\left ( \frac{x-y}{2} \right )$

$\dpi{120} sin75+sin15=2sin\left ( \frac{75+15}{2} \right )cos\left ( \frac{75-15}{2} \right )$

= 2sin(45) cos(30)

$\dpi{120} =2*\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{2}$

Practice problems:

Find the exact value of cos(13π/12).
Find the exact value of sin(u+v) given that sinu=-7/25 and cosv =-4/5 (Both u and v are in quadrant III)
Find the exact value of expression $\dpi{120} cos\left (\frac{3\pi }{4} \right )-cos\left ( \frac{\pi }{4} \right )$
Write the following trigonometric expression as an algebraic expression.

$\dpi{120} sin\left [ tan^{-1}(2x)-cos^{-1}(x) \right ]$

Prove the identity.

Cos(x+y)cos(x-y) = cos^2(x)-cos^2(y)

Answers:

$\dpi{120} \frac{-\sqrt{6}-\sqrt{2}}{4}$
-4/5
-√2
$\dpi{120} \frac{2x^{2}-\sqrt{1-x^{2}}}{\sqrt{1+4x^{2}}}$

Degree, Radians and their Conversions

September 5, 2019/by admin_ct

Degree, Radians and their conversions

Angle is generally measured in degrees or radians. Degree is written using symbol (° ) and radians is written without any symbol. 360° make up one circle.

Radian: one radian is the measure of an angle subtended at the centre of circle by an arc length equal to radius of circle.

Using this we have relation as,

$\dpi{120} \mathbf{\theta =\frac{s(arc length)}{r(radius)}}$

Relation among three measures of angles:

360° = 2π radians = 1 revolution

Here is an useful table showing relation among the three measures of angle(revolutions, degrees and radians)

words	rev	deg	rad

no turn	0	0°	0
quarter turn	1/4	90°	π/2
half turn	1/2	180°	π
three-quarter turn	3/4	270°	3π/2
full turn	1	360°	2π

Revolutions(turns) are a more natural unit of measure than degrees. To convert revolutions to degrees we multiply with 360 and to convert degree to revolutions we divide by 360.

Radians and degree conversion :

We know that,

360° = 2π

1° = 2π/360 = π/180

To convert degree to radians we multiply with π/180 and to convert radians to degrees we multiply with 180/π .

DEGREES to RADIANS: RADIANS to DEGREES :

Degree*π/180 = Radians Radians*180/π = Degrees

Example: Example:

120° =120*(π/180) = 2π/3 3π/4 =(3π/4)*(180/π) =3*45=135°

Example: Convert the following degrees into radians.

Solution: a) 22.5°

$\dpi{120} 22.5^{\circ}=\frac{225}{10}*\frac{\pi }{180}=\frac{225\pi }{1800}=\frac{\pi }{8}$

b) 315°

$\dpi{120} 315^{\circ}=315 *\frac{\pi }{180}=\frac{315\pi }{180}=\frac{7\pi }{4}$

Example : Convert the following radians into degrees.

Solution: a) 2π/15

$\dpi{120} \frac{2\pi }{15}=\frac{2\pi }{15}*\frac{180}{\pi }=\frac{360}{15}=24^{\circ}$

b) 7π/8

$\dpi{120} \frac{7\pi }{8}=\frac{7\pi }{8}*\frac{180}{\pi }=\frac{1260}{8}=157.5^{\circ}$

An angle in degrees can be written completely using minutes and seconds. As

1 = 60minutes (‘)

1’ = 60 seconds (”)

Lets work on some examples on how to convert radians into degrees, minutes and seconds.

Example: Convert the following radian measures into degree, minutes and seconds.

Solution:

a) π/8

$\dpi{120} \frac{\pi }{8}*\frac{180}{\pi }=\frac{45}{2}= \left (22\frac{1}{2} \right )^{\circ}=22^{\circ}\left ( \frac{1}{2}*60 \right )'=22^{\circ}30'$

b) 1/4

$\dpi{120} \frac{1}{4}*\frac{180}{\pi }=\frac{45}{\pi }=\left ( 45*\frac{7}{22} \right )=\left (\frac{315}{22} \right )^{\circ}=\left ( 14\frac{7}{22} \right )^{\circ}=14^{\circ}\left ( \frac{7}{22}*60 \right )'$

$\dpi{120} = 14^{\circ}\left ( 19\frac{1}{11} \right )'=14^{\circ}19'\left ( \frac{1}{11}*60 \right )''= 14^{\circ}19'\left ( \frac{60}{11} \right )''=14^{\circ}19'5''$

c) -2

$\dpi{120} -2 *\frac{180}{\pi }=\left ( \frac{-2*7*180}{22} \right )^{\circ}=\left ( -114\frac{6}{11} \right )^{\circ}=-114^{\circ}\left ( \frac{6}{11}*60 \right )'$

$\dpi{120} =-114^{\circ}\left ( 32\frac{8}{11} \right )'=-114^{\circ}32'\left ( \frac{8}{11}*60 \right )''=-114^{\circ}32'44''$

Convert minutes and seconds into degrees

$\dpi{120} 1'=\left ( \frac{1}{60} \right )^{\circ}$

$\dpi{120} 1''= \left ( \frac{1}{60} \right )'= \left ( \frac{1}{3600} \right )^{\circ}$

Lets work on some examples on how to convert minutes and seconds into degrees . Here is a video example.

Example : Convert the following degree, minutes and seconds into decimal degrees.

Solution:

1) 25°12′

$\dpi{120} 25^{\circ}12'= 25^{\circ}+\left ( \frac{12}{60} \right )^{\circ}=25^{\circ}+0.2^{\circ}=25.2^{\circ}$

2) 42°15’45”

$\dpi{120} 42^{\circ}15'45''=42^{\circ} +\left (15* \frac{1}{60} \right )^{\circ}+\left ( 45*\frac{1}{3600} \right )^{\circ}$

= 42° + 0.25° + 0.0125° = 42.2625°

Practice problems:

Convert the given angle measures from radians into degrees

18π/5
11

Convert the given angle measures from degrees to radians

–56°
47.5°

Convert the given angle measures from radians to degrees,

Minutes and seconds

6
π/32

Convert the given angle measures from degree, minutes and seconds to degrees only

40°20‘
5°37‘30”

Answers:

648°
630°
–14π/45
19π/72
343°38‘11”
5°37‘30”
(121/3)°
(45/8)°

De Moivre’s Theorem and nth Roots

September 2, 2019/by admin_ct

De Moivre’s Theorem and nth Roots

Complex plane :

Just as real numbers can be represented by points on the real number line, we can represent a complex number z= x+yi as a point (x,y) in the complex plane.

The horizontal axis is called real axis and vertical axis is called imaginary axis.

Example1. Plot u=1+3i , v=2-i , and u+v in the complex plane. These three points and the origin determine a quadrilateral. Is it a parallelogram?

Solution: u=1+3i , v=2-i

u+v =(1+3i) + (2- i) =2+3i

Now we plot these points 1+3i, 2-i and 2+3i in complex plane as shown below.

Figure (a) shows numbers plotted in complex plane and figure (b) shows that arithmetic is same as in vector addition.

The quadrilateral is a parallelogram because the arithmetic is exactly the same as in vector addition.

Trigonometric Form of Complex Numbers

The trigonometric form of a complex number is also called the polar form.

Because there are infinitely many choices for θ , the trigonometric form of a complex number is not unique. Normally, is restricted to the interval 0≤θ≤2π although on occasion it is convenient to θ<0.

Example2. Find the trigonometric form of the complex number where the argument satisfies 0≤θ≤2π.

Z = -2+ 2√3 i

Solution: The absolute value of z is,

$\dpi{120} r= \left | -2+2\sqrt{3}i \right |=\sqrt{(-2)^{2}+(2\sqrt{3})^{2}}= \sqrt{16}=4$

Argument $\dpi{120} tan\theta =\frac{2\sqrt{3}}{-2}= -\sqrt{3}$

$\dpi{120} \theta =tan^{-1}(-\sqrt{3})= \frac{2\pi }{3}$

So the polar form is

$\dpi{120} z = 4\left [ cos\frac{2\pi }{3}+ isin\frac{2\pi }{3} \right ]$

Multiplication and Division of Complex Numbers

The trigonometric form for complex numbers is particularly convenient for multiplying and dividing complex numbers. The product involves the product of the moduli and the sum of the arguments. (Moduli is the plural of modulus.) The quotient involves the quotient of the moduli and the difference of the arguments.

Product of two complex numbers:

Let $\dpi{120} z_{1}=r_{1}(cos\theta _{1}+i sin\theta _{1})$

And $\dpi{120} z_{2}=r_{2}(cos\theta _{2}+i sin\theta _{2})$

then product is given as,

$\dpi{150} \mathbf{z_{1}z_{2}=r_{1}r_{2}\left [ cos(\theta _{1}+\theta _{2})+i sin(\theta _{1}+\theta _{2}) \right ]}$

Example3. Find the product in two ways, (a) using the trigonometric form for z1 and z2 and (b) using the standard form for z1 and z2 .

Z1 = 3-2i Z2 = 1+i

Solution: a) we need to convert the two numbers into trigonometric form.

For Z1, $\dpi{120} r_{1}=\sqrt{(3)^{2}+(-2)^{2}}=\sqrt{13}$

$\dpi{120} \theta _{1}=tan^{-1}\left ( \frac{-2}{3} \right )=326.31$

For Z2, $\dpi{120} r_{2}=\sqrt{(1)^{2}+(1)^{2}}=\sqrt{2}$

$\dpi{120} \theta _{2}=tan^{-1}\left ( \frac{1}{1} \right )= 45^{\circ}$

$\dpi{120} z_{1}z_{2}=\sqrt{13}\sqrt{2}\left [ cos(326.31+45)+i sin(326.31+45) \right ]$

$\dpi{120} z_{1}z_{2}=\sqrt{26}\left [ cos(371.31)+i sin(371.31) \right ]$

= 4.9999 + 1.000 i

= 5 + i

b) algebraic method

Z1Z2 = (3-2i)*(1+i)

= 3 + 3i -2i -2i(i)

= 3 + i -2(-1) = 3 + i +2

= 5 + i

Quotient of Two Complex Numbers

Let $\dpi{120} z_{1}=r_{1}(cos\theta _{1}+i sin\theta _{1})$

And $\dpi{120} z_{2}=r_{2}(cos\theta _{2}+i sin\theta _{2})$

then quotient is given as,

$\dpi{150} \mathbf{\frac{z_{1}}{z_{2}}= \frac{r_{1}}{r_{2}}\left [ cos(\theta _{1}-\theta _{2})+isin\left ( \theta _{1}-\theta _{2} \right ) \right ] , r_{2}\neq 0}$

Example4. Find the quotient in two ways, (a) using the trigonometric form for Z1 and Z2 and (b) using the standard form for Z1 and Z2 .

Z1 = 3 + i Z2 = 5 – 3i

Solution: First we convert the two numbers into trigonometric form.

For Z1 , $\dpi{120} r_{1}=\sqrt{(3)^{2}+(1)^{2}}=\sqrt{10}$

$\dpi{120} \theta _{1}=tan^{-1}\left ( \frac{1}{3} \right )=18.43$

For Z2 , $\dpi{120} r_{2}=\sqrt{(5)^{2}+(-3)^{2}}=\sqrt{34}$

$\dpi{120} \theta _{2}=tan^{-1}\left ( \frac{-3}{5} \right )= 329.04^{\circ}$

$\dpi{120} \frac{z_{1}}{z_{2}}= \frac{\sqrt{10}}{\sqrt{34}}\left [ cos(18.43-329.04)+isin\left ( 18.43-329.04 \right ) \right ]$

= 0.54232[ 0.6509 + i 0.7591]

= 0.35 + 0.41 i

b) By algebraic method

$\dpi{120} \frac{z_{1}}{z_{2}}=\frac{3+i}{5-3i}*\frac{5+3i}{5+3i}=\frac{(3+i)(5+3i)}{(5-3i)(5+3i)}$

$\dpi{120} =\frac{15+9i+5i+3i^{2}}{5^{2}-(3i)^{2}}=\frac{15+14i-3}{25+9}$

$\dpi{120} =\frac{12+14i}{34}= 0.35+0.41i$

De Moivre’s Theroem

This theorem is used to raise a complex number to a power.

Let $\dpi{120} \mathbf{z=r\left [ cos\theta +isin\theta \right ]}$ and let n be a positive integer, then

$\dpi{150} \mathbf{Z^{n}=\left [ r(cos\theta +isin\theta ) \right ]^{n}= r^{n}\left [ cos(n\theta )+isin(n\theta ) \right ]}$

Example5: Use De Moivre’s Theorem to find the indicated power of the complex number. Write your answer in standard form.

$\dpi{150} {\color{Red} (1-\sqrt{3}i)^{3}}$

Solution: First we need to find trigonometric form of given complex number.

Z = 1-√3 i

$\dpi{120} r=\sqrt{(1)^{2}+(-\sqrt{3})^{2}}=\sqrt{4}=2$

$\dpi{120} \theta =tan^{-1}\left ( \frac{-\sqrt{3}}{1} \right )=\frac{5\pi }{3}$

Z = 2[ cos(5π/3) + i sin(5π/3) ]

Using De Moivre’s theorem,

$\dpi{120} z^{3}=\left [ 2\left (cos\frac{5\pi }{3}+isin\frac{5\pi }{3} \right ) \right ]^{3}$

$\dpi{120} =2^{3}\left [ cos(3*\frac{5\pi }{3})+isin\left ( 3*\frac{5\pi }{3} \right ) \right ]$

= 8 [cos 5π + i sin 5π ]

= 8 [ -1 + 0i] = -8

Finding nth Roots of a Complex Number

If $\dpi{120} \mathbf{z=r\left [ cos\theta +isin\theta \right ]}$ , then the n distinct complex numbers

$\dpi{150} \mathbf{\sqrt[n]{r}\left [ cos\left ( \frac{\theta +2\pi k}{n} \right )+isin\left ( \frac{\theta +2\pi k}{n} \right ) \right ]}$

Where k= 0,1,2,3….n-1, are the nth roots of complex number z.

Example6. Find cube roots of complex number

$\dpi{120} {\color{Red} z=3[cos\frac{4\pi }{3}+isin\frac{4\pi }{3}]}$

Solution: Using nth root formula,

$\dpi{120} \sqrt[n]{r}\left [ cos\left ( \frac{\theta +2\pi k}{n} \right )+isin\left ( \frac{\theta +2\pi k}{n} \right ) \right ]$

Plug in n=3 , r=3 and θ=4π/3

$\dpi{120} \sqrt[3]{3}\left [ cos\left ( \frac{\frac{4\pi }{3} +2\pi k}{3} \right )+isin\left ( \frac{\frac{4\pi }{3} +2\pi k}{3} \right ) \right ]$

$\dpi{120} \sqrt[3]{3}\left [ cos\left ( \frac{4\pi }{9}+\frac{2\pi k}{3} \right )+isin\left ( \frac{4\pi }{9}+\frac{2\pi k}{3} \right ) \right ]$

Now we can find cube roots using k=0,1 and 2

$\dpi{120} Z_{1}=\sqrt[3]{3}\left [ cos\left ( \frac{4\pi }{9}+\frac{2\pi (0)}{3} \right )+isin\left ( \frac{4\pi }{9}+\frac{2\pi (0)}{3} \right ) \right ]$

$\dpi{120} Z_{1}=\sqrt[3]{3}\left [ cos\left ( \frac{4\pi }{9} \right )+isin\left ( \frac{4\pi }{9}\right ) \right ]$

$\dpi{120} Z_{2}=\sqrt[3]{3}\left [ cos\left ( \frac{4\pi }{9}+\frac{2\pi (1)}{3} \right )+isin\left ( \frac{4\pi }{9}+\frac{2\pi (1)}{3} \right ) \right ]$

$\dpi{120} Z_{2}=\sqrt[3]{3}\left [ cos\left ( \frac{10\pi }{9} \right )+isin\left ( \frac{10\pi }{9}\right ) \right ]$

$\dpi{120} Z_{3}=\sqrt[3]{3}\left [ cos\left ( \frac{4\pi }{9}+\frac{2\pi (2)}{3} \right )+isin\left ( \frac{4\pi }{9}+\frac{2\pi (2)}{3} \right ) \right ]$

$\dpi{120} Z_{3}=\sqrt[3]{3}\left [ cos\left ( \frac{16\pi }{9} \right )+isin\left ( \frac{16\pi }{9}\right ) \right ]$

Example7. Find the cube roots of -1 .

Solution: First we write the complex number z=-1 in trigonometric form.

Z = -1 +0i = cosπ + i sinπ

The third roots of this complex number using r=1, θ=π and n=3 is written as,

$\dpi{120} \sqrt[3]{1}\left [ cos\left ( \frac{\pi +2\pi k}{3} \right )+isin\left ( \frac{\pi +2\pi k}{3} \right ) \right ]$

Using k=0,1,2 we get the three cube roots as

$\dpi{120} Z_{1}=\sqrt[3]{1}\left [ cos\left ( \frac{\pi +2\pi (0)}{3} \right )+isin\left ( \frac{\pi +2\pi (0)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[3]{1}\left [ cos\frac{ \pi }{3}+isin\frac{\pi }{3} \right ]=\frac{1}{2}+\frac{\sqrt{3}}{2}i$

$\dpi{120} Z_{2}=\sqrt[3]{1}\left [ cos\left ( \frac{\pi +2\pi (1)}{3} \right )+isin\left ( \frac{\pi +2\pi (1)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[3]{1}\left [ cos \pi +isin\pi \right ]= -1+0i$

$\dpi{120} Z_{3}=\sqrt[3]{1}\left [ cos\left ( \frac{\pi +2\pi (2)}{3} \right )+isin\left ( \frac{\pi +2\pi (2)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[3]{1}\left [ cos\frac{ 5\pi }{3}+isin\frac{5\pi }{3} \right ]=\frac{1}{2}-\frac{\sqrt{3}}{2}i$

Example8. Find the nth roots of the complex number for the specified value of n.

z = -2i , n=6

Solution: z = 0 -2i

$\dpi{120} r=\sqrt{(0)^{2}+(-2)^{2}}=2$

$\dpi{120} \theta =tan^{-1}\left ( \frac{2}{0} \right )= \frac{3\pi }{2}$ (point lying on negative y axis)

Plugin r=2 , θ=3π/2 and n=6 into following formula

$\dpi{120} \sqrt[n]{r}\left [ cos\left ( \frac{\theta +2\pi k}{n} \right )+isin\left ( \frac{\theta +2\pi k}{n} \right ) \right ]$

We get

$\dpi{120} \sqrt[6]{2}\left [ cos\left ( \frac{\frac{3\pi }{2} +2\pi k}{6} \right )+isin\left ( \frac{\frac{3\pi }{2} +2\pi k}{6} \right ) \right ]$

$\dpi{120} \sqrt[6]{2}\left [ cos \left ( \frac{\pi }{4}+\frac{\pi k}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi k}{3} \right ) \right ]$

$\dpi{120} Z_{1}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (0)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (0)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{\pi }{4} +isin\frac{\pi }{4}\right ]=\sqrt[6]{2}\left ( \frac{\sqrt{2}}{2} +\frac{\sqrt{2}}{2}i\right )$

$\dpi{120} Z_{2}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (1)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (1)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{7\pi }{12} +isin\frac{7\pi }{12}\right ]$

$\dpi{120} Z_{3}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (2)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (2)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{11\pi }{12} +isin\frac{11\pi }{12}\right ]$

$\dpi{120} Z_{4}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (3)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (3)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{5\pi }{4} +isin\frac{5\pi }{4}\right ]$

$\dpi{120} Z_{5}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (4)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (4)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{19\pi }{12} +isin\frac{19\pi }{12}\right ]$

$\dpi{120} Z_{6}=\sqrt[6]{2}\left [ cos\left ( \frac{\pi }{4}+\frac{\pi (5)}{3} \right )+isin\left ( \frac{\pi }{4}+\frac{\pi (5)}{3} \right ) \right ]$

$\dpi{120} =\sqrt[6]{2}\left [ cos\frac{23\pi }{12} +isin\frac{23\pi }{12}\right ]$

Example9. Determine z and the three cube roots of z if one cube root of z is 1 + √3 i

Solution: Given cube root of z = 1+ √3i

Therefore, $\dpi{120} z^{\frac{1}{3}}=1+\sqrt{3}i$

$\dpi{120} z=\left ( 1+\sqrt{3}i \right )^{3}$

After expanding cube we get,

$\dpi{120} z= 1+3\sqrt{3}i^{3}+3\sqrt{3}i+9i^{2}$

= 1-3 i +3 i – 9

= -8

For complex number z= -8+0i we have r=8 and θ=π , n=3

Plugin these values into formula

$\dpi{120} \sqrt[n]{r}\left [ cos\left ( \frac{\theta +2\pi k}{n} \right )+isin\left ( \frac{\theta +2\pi k}{n} \right ) \right ]$

$\dpi{120} \sqrt[3]{8}\left [ cos\left ( \frac{\pi +2\pi k}{3} \right )+isin\left ( \frac{\pi +2\pi k}{3} \right ) \right ]$

Using k=0,1,2 for three cube roots

$\dpi{120} Z_{1}=\sqrt[3]{8}\left [ cos\left ( \frac{\pi +2\pi (0)}{3} \right )+isin\left ( \frac{\pi +2\pi (0)}{3} \right ) \right ]$

$\dpi{120} =2\left [ cos\frac{\pi }{3}+isin\frac{\pi }{3} \right ]= 2\left ( \frac{1}{2}+\frac{\sqrt{3}}{2}i \right )= 1+\sqrt{3}i$

$\dpi{120} Z_{2}=\sqrt[3]{8}\left [ cos\left ( \frac{\pi +2\pi (1)}{3} \right )+isin\left ( \frac{\pi +2\pi (1)}{3} \right ) \right ]$

$\dpi{120} =2\left [ cos\pi +isin \pi \right ]= -2+0i$

$\dpi{120} Z_{3}=\sqrt[3]{8}\left [ cos\left ( \frac{\pi +2\pi (2)}{3} \right )+isin\left ( \frac{\pi +2\pi (2)}{3} \right ) \right ]$

$\dpi{120} =2\left [ cos\frac{5\pi }{3}+isin\frac{5\pi }{3} \right ]= 2\left ( \frac{1}{2}-\frac{\sqrt{3}}{2}i \right )= 1-\sqrt{3}i$

Practice problems:

Find the trigonometric form of given complex number.

Z = 3i

2. Write the complex number in standard form.

5[cos(-60)+ i sin(-60)

3. Find the product Z1*Z2 and quotient Z1/Z2 in two ways,

(a) using the trigonometric form for Z1 and Z2 and

(b) using the standard form for Z1 and Z2.

Z1 = 3 + i Z2 = 5 – 3i

4. Find fifth roots of given complex number

Cosπ + i sinπ

Answers:

3(cos(π/2) + i sin(π/2) )
$\dpi{120} \frac{5}{2}-\frac{5\sqrt{3}}{2}i$
a) 18-4i , 0.35 +0.41i b) same as part a

$\dpi{120} cos\frac{\pi }{5}+isin\frac{\pi }{5} , cos\frac{3\pi }{5}+isin\frac{3\pi }{5} , cos\frac{7\pi }{5}+isin\frac{7\pi }{5},cos\frac{9\pi }{5}+isin\frac{9\pi }{5}$

Co-terminal Angles

September 2, 2019/by admin_ct

Co-terminal angles

Lets be familiar with some basic concepts before moving on to co terminal and reference angles.

Unit circle is a circle of radius 1.That’s why it is called unit circle.
For positive angle move anticlockwise around the circle starting from positive x axis.
For negative angle move clockwise around the circle starting from positive x axis.
One complete revolution =360° or 2π radians.
Two complete revolutions = 720° or 4π radians.

Co terminal angles :

The angles which share the same initial and terminal sides , initial side being the positive x axis.

There are infinite number of co terminal angles that can be found for any given angle.

Coterminal angle for angle less than 360.

To find positive co terminal angle of any given angle we add 360 or multiple of 360.

To find negative co terminal angle we subtract 360 or multiple of 360.

If angle is in radians then we use 2π in place of 360.

Example : Find a positive and negative co terminal angle for each of the following angles.

50° b) -120° c) 2π/3

Solution:

Positive co terminal : 50+360= 410°

Negative co terminal : 50- 360 = -310°

2. -120

Positive co terminal angle : -120+360 =240°

Negative co terminal angle: -120-360= -480°

3. 2π/3

Positive co terminal angle: $\dpi{120} \frac{2\pi }{3}+2\pi = \frac{8\pi }{3}$

Negative co terminal angle : $\dpi{120} \frac{2\pi }{3}-2\pi = \frac{-4\pi }{3}$

Co terminal angle for angles greater than 360.

Keep on adding or subtracting 360 from the given angle until we reach at an angle which is less than 360 .

We can also subtract or add any multiple of 360 depending on the given angle value.

Examples: Find a positive and negative co terminal angles for each of the given angles.

a) 875 b)-1120

Solution:

a)875

To find positive co terminal angle we keep on subtracting 875 until we get an angle less than 360.

875-360 = 515

515-360 = 155

Or we can also subtract suitable multiple of 360

875-2(360) = 875-720 => 155

To find negative co terminal angle we subtract further 360 from 155 and get 155-360= -205°

b) -1120

To find negative co terminal angle keep on adding 360 to get an angle less than 360.

-1120 + 360= -760

-760+360 = -400

-400+360= -40

or we can add a suitable multiple of 360

-1120 +3(360)= -40

To find positive coterminal angle we further add 360 to -40

So positive coterminal angle is -40+360 = 320

Two angles are coterminal if the difference between them is a multiple of 360° or 2π.

Example: Determine if the following pairs of angles are coterminal.

30 and 390
120 and 450
-260 and 100

Solution:

30-390= -360 So this pair is coterminal.
120 -450= -330 This pair is not coterminal.
-260-100 =-360 This pair is coterminal.

Practice problems:

Find a coterminal angle for each of the following angles:

-330
245
-7π/6
3π/4

2. Find a positive and negative coterminal angle for each of the following.

11π/3
-5π/6
735
-1230

3. Determine if the following pairs of angles are coterminal.

-300 and -60
450 and 90
-340 and 70

Answers: 1)

30
-115
5π/6
-5π/4

1) positive : 5π/3 negative : -π/3

2) positive : 7π/6 negative : -17π/6

3) positive: 15 negative : -345

4) positive :210 negative : -150

1) No

2) Yes

3) No

Applications of Right triangle Trigonometry

September 1, 2019/by admin_ct

Applications of Right triangle Trigonometry

Right triangle trigonometry is used to find height and distances of various objects without actually measuring them. Before moving to this topic, first we need to understand the terms Angle of Elevation and Angle of Depression.

An angle of elevation is the angle through which the eye moves up from horizontal to look at something above, and an angle of depression is the angle through which the eye moves down from horizontal to look at something below.

Before moving to applications of right triangle trigonometry we should know how to convert degree minutes and seconds into decimal degrees.

Degree Decimals = degrees+ (minutes/60) +(seconds/3600)

Example:

$\dpi{120} 35^{\circ}15'45''= 35 +\frac{15}{60}+\frac{45}{3600} =35+0.25+0.0125=35.2625^{\circ}$

Example1. To measure the height of a cloud, you place a bright searchlight directly below the cloud and shine the beam straight up. From a point 100 ft away from the searchlight, you measure the angle of elevation of the cloud to be 83°12’ . How high is the cloud?

Solution:

First we convert 83° 12’ into decimal degrees and get,

83°12’ = 83+(12/60)=83.2°

Lets assume h as height of cloud C from search light A.

In right triangle ABC

$\dpi{120} \frac{opposite}{Adjacant}=tan\theta$

$\dpi{120} \frac{h}{100}=tan(83.2^{\circ})$

h = 100tan(83.2)

h = 838.625 ≈ 839 ft.

Example2. The angle of elevation from an observer to the bottom edge of the Delaware River drawbridge observation deck located 200 ft from the observer is 30° . The angle of elevation from the observer to the top of the observation deck is 40°. What is the height of the observation deck?

Solution:

In the figure drawn above AB is the observation deck with height as h, which we need to find.

In right triangle ACD

$\dpi{120} \frac{h+x}{200}=tan(40)$

h+x = 200 tan(40)———-(i)

In right triangle BCD

$\dpi{120} \frac{x}{200}=tan(30)$

x = 200tan(30) ———–(ii)

Substituting x as 200tan(30) into equation(i) we get,

h+ 200tan(30)=200tan(40)

h = 200tan(40)-200tan(30)

h = 200(tan40-tan30)

h = 52.3498 52.35 ft.

Example3. The angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line are complementary. Find the height of tower.

Solution:

In the figure drawn above AB is the tower and C, D are the points at 4m and 9m from the base of tower.

As the angles are complementary, so one angle is θ and other angle is 90-θ.

In right triangle ABC

$\dpi{120} \frac{AB}{4}=tan\theta$

In right triangle ABD

$\dpi{120} \frac{AB}{9}=tan(90-\theta )$

$\dpi{120} \frac{AB}{9}=cot\theta$ [tan(90-θ) = cotθ ]

Multiplying both the equations we get,

$\dpi{120} \frac{AB}{4}*\frac{AB}{9}=tan\theta *cot\theta$

$\dpi{120} \frac{AB^{2}}{36 }=tan\theta *\frac{1}{tan\theta }$

$\dpi{120} \frac{AB^{2}}{36}=1$

$\dpi{120} AB^{2}=36$

AB = 6

As the height can’t be negative , so dropping negative sign we get height of tower as 6m.

Example4. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of tower.

Solution:

In the figure drawn below AB is the building of height 7 m and CE is the tower whose height we need to find.

Also, AB=CD= 7m

In right triangle ABC

7/ BC = tan(45)

7/BC = 1 => BC = 7m

AD = BC = 7m

In right triangle ADE

DE/AD = tan(60)

DE/7 = √3

DE = 7√3

Height of tower CE= CD+DE

CE = 7+7√3 ≈ 19.12m

Example5. The Cerrito Lindo travels at a speed of 40 knots from Fort Lauderdale on a course of 65° for 2 hr and then changes to a course of 155° for 4 hr. Determine the distance and the bearing from Fort Lauderdale to the boat.

Solution: The figure drawn below models the situation.

Assuming AB a transversal line that cuts two parallel lines , we get alternate interior angle same as 65 and 25 is the supplement angle of 155. Consequently we get < ABC =90° and AC is the hypotenuse of right triangle ABC.

Using distance= speed* time formula we get,

AB= 40*2 = 80 nautical miles

BC = 40*4= 160 nautical miles

Using Pythagorean,

$\dpi{120} AC=\sqrt{AB^{2}+BC^{2}}$

$\dpi{120} AC=\sqrt{80^{2}+160^{2}}$

= √32000 = 178.88 nautical miles

$\dpi{120} \theta =tan^{-1}(\frac{160}{80}) =63.43$

Bearing of boat from Fort Lauder would be 65°+θ which is

65°+63.43 = 128. 43°

Example6. Milwaukee, Wisconsin, is directly west of Grand Haven, Michigan, on opposite sides of Lake Michigan. On a foggy night, a law enforcement boat leaves from Milwaukee on a course of 105° at the same time that a small smuggling craft steers a course of 195°from Grand Haven. The law enforcement boat averages 23 knots and collides with the smuggling craft. What was the smuggling boat’s average speed?

Solution: The figure drawn below models the given situation.

Enforcement boat is moving from A to C at the speed of 23 knots. Lets assume smuggling boat is moving from B to C at a speed of x knots.

Since the time travelled is same for both the boats so distances travelled would also be in same ratio as their speeds.

In right triangle ABC, using θ =15

BC/AC = tan(θ)

x/23 = tan(15)

x = 23 tan(15) = 6.16 knots

Practice problems:

From the top of the 100-ft-tall Altgelt Hall a man observes a car moving toward the building. If the angle of depression of the car changes from 22° to 46°during the period of observation, how far does the car travel?
A ramp leading to a freeway overpass is 470 ft long and rises 32 ft. What is the average angle of inclination of the ramp to the nearest tenth of a degree?
The angle of depression is 19° from a point 7256 ft above sea level on the north rim of the Grand Canyon level to a point 6159 ft above sea level on the south rim. How wide is the canyon at that point?
A shoreline runs north-south, and a boat is due east of the shoreline. The bearings of the boat from two points on the shore are 110°and 100°. Assume the two points are 550 ft apart. How far is the boat from the shore?

Answers:

151 ft.
3.9°
3186 ft.
2931 ft.

All Basic Trigonometric functions

August 31, 2019/by admin_ct

Basic trigonometric functions

Let θ be an angle in standard position with (x,y) a point on the terminal side of angle θ and $\dpi{120} r=\sqrt{x^2+y^2}\neq 0$

Sinθ = y/r Cosec = r/y

Cosθ = x/r Secθ = r/x

Tanθ = y/x Cotθ = x/y

Since r can’t be 0 so sine and cosine are defined for every real value of . However if x=0, then tan and sec are undefined. Similarly if y=0, then cosec and cot are undefined.

Example: Given point (-3,4) on terminal side of an angle in standard position. Determine the exact value of all six trigonometric functions.

Solution: From given point (x, y)= (-3,4), we have x=-3 and y= 4

$\dpi{120} r=\sqrt{x^2+y^2}$

$\dpi{120} r=\sqrt{(-3)^2+(4)^2}=\sqrt{25}=5$

So, we have the functions as follows:

Sinθ = 4/5 Cosecθ = 5/4

Cosθ = – 3/5 Secθ = – 5/3

Tanθ = – 4/3 Cot = – 3/4

ASTC rule:

X and Y axis divide whole space in 4 parts called quadrants. To know the sign of trigonometric ratios in these different quadrants, we use ASTC rule. We can use any mnemonic to memorize this rule like “ All Students Take Calculus” or “Add Sugar To Coffee”

All trigonometric ratios positive in first quadrant.

Only Sin and its reciprocal Cosec are positive in 2^nd quadrant, rest all are negative.

Only Tan and its reciprocal cot are positive in 3^rd quadrant , rest all are negative.

Only Cos and its reciprocal Sec are positive in 4^th quadrant, rest all are negative.

Quadrants	Range in degrees	Range in radians.
I	0 -90°	$\dpi{120} 0- \frac{\pi }{2}$
II	90° -180°	$\dpi{120} \frac{\pi }{2}-\pi$
III	180° -270°	$\dpi{120} \pi -\frac{3\pi }{2}$
IV	270° -360°	$\dpi{120} \frac{3\pi }{2}-2\pi$

Example: Find the values of the other five trigonometric functions of θ with given function value .

$\dpi{120} {\color{Red} tan\theta =- \frac{15}{8}}$ and constraint sinθ >0.

Solution: Note that tan is negative and sin is positive which is possible only in 2^nd quadrant.

Given that $\dpi{120} tan\theta =- \frac{15}{8}$

$\dpi{120} \frac{y}{x}=-\frac{15}{8}$

In 2^nd quadrant x is negative and y is positive.

So x=-8 and y= 15

Therefore $\dpi{120} r=\sqrt{(-8)^2+(15)^2}=\sqrt{289}= 17$

Sinθ = 15/17 Cosecθ = 17/15

Cosθ = -8/17 Secθ = – 17/8

Tanθ = -15/8 Cot = – 8/15

Since angle was in second quadrant, so we got only sin and cosec positive and rest all negative.

Example: If cosθ=-1/2 and $\dpi{120} {\color{Red} \pi <\theta <\frac{3\pi }{2}}$ then find the value of $\dpi{120} {\color{Red} 4tan^{2}\theta -3csc^{2}\theta }$

Solution: Since θ lies in third quadrant, therefore sin is negative and tan is positive.

Using basic Pythagorean identities given in previous section, we have,

$\dpi{120} sin\theta =\pm \sqrt{1-cos^{2}\theta }$

$\dpi{120} sin\theta =-\sqrt{1-\left ( \frac{-1}{2} \right )^{2} }$

$\dpi{120} sin\theta =-\sqrt{1-\frac{1}{4}} =-\sqrt{\frac{3}{4}} =-\frac{\sqrt{3}}{2}$

$\dpi{120} csc\theta =\frac{-2}{\sqrt{3}}$

Using basic trigonometric identities we have,

$\dpi{120} tan\theta =\frac{sin\theta }{cos\theta }= -\frac{\sqrt{3}}{2}*\frac{-2}{1}=\sqrt{3}$

$\dpi{120} 4tan^{2}\theta -3csc^{2}\theta = 4\left ( \sqrt{3} \right )^{2}-3\left ( \frac{-2}{\sqrt{3}} \right )^{2}$

=4(3)-3(4/3) = 12-4 = 8

Practice problems:

Given point (5,-12) on terminal side of an angle in standard position. Determine the exact value of all six trigonometric functions.
Find the values of the other five trigonometric functions of θ with given function value cosθ = -12/13 and constraint sinθ < 0.
If cosθ =-3/5 and $\dpi{120} \pi <\theta <\frac{3\pi }{2}$ then find the value of $\dpi{120} \frac{csc\theta +cot\theta }{sec\theta -tan\theta }$

Answers:

sin =-12/13 ,cos =5/13 ,tan =-12/5 ,cosec =-13/12 ,sec =13/5 , cot =-5/12
sin =-5/13 ,tan =5/12 ,cosec =-13/5 ,sec =-13/12 , cot =12/5
1/6

All Trigonometric Identities and Formulas

August 31, 2019/by admin_ct

All Trigonometric Identities and Formulas

Trigonometric identities are those equations which are true for all those angles for which functions are defined.

The equation sinθ = cosθ is a trigonometric equation but not a trigonometric identity because it doesn’t hold for all values of There are some fundamental trigonometric identities which are used to prove further complex identities.

Here is a list of all basic identities and formulas.

Pythagorean identities:

$\dpi{120} \mathbf{sin^{2}\theta +cos^{2}\theta =1}$
$\dpi{120} \mathbf{1+tan^{2}\theta =sec^{2}\theta }$
$\dpi{120} \mathbf{1+cot^{2}\theta =csc^{2}\theta}$

Reciprocal identities:

$\dpi{120} \mathbf{sin\theta =\frac{1}{csc\theta } }$ or $\dpi{120} \mathbf{csc\theta =\frac{1}{sin\theta }}$
$\dpi{120} \mathbf{cos\theta =\frac{1}{sec\theta }}$ or $\dpi{120} \mathbf{sec\theta =\frac{1}{cos\theta }}$
$\dpi{120} \mathbf{tan\theta =\frac{1}{cot\theta }}$ or $\dpi{120} \mathbf{cot\theta =\frac{1}{tan\theta }}$

Quotient identities:

$\dpi{120} \mathbf{tan\theta =\frac{sin\theta }{cos\theta }}$ or $\dpi{120} \mathbf{cot\theta =\frac{cos\theta }{sin\theta }}$

Even-Odd identities:

Only cos and sec are even functions ,rest are all odd.

Even: cos(-x) = cos(x) sec(-x) = sec(x)

Odd: sin(-x) =-sin(x) csc(-x) =-csc(x)

tan(-x)=-tan(x) cot(-x) =-cot(x)

Sum and difference formulas:

sin(u±v) = sin(u)cos(v)±cos(u)sin(v)
cos(u±v) = cos(u)cos(v)∓sin(u)sin(v)
$\dpi{120} \mathbf{tan(u\pm v)=\frac{tan(u)\pm tan(v)}{1\mp tan(u)tan(v)}}$

Double angle identities:

sin(2θ)= 2sinθ cosθ

$\dpi{120} \mathbf{cos(2\theta )= cos^{2}\theta -sin^{2}\theta }$

$\dpi{120} \mathbf{cos(2\theta )=2cos^{2}\theta -1}$

$\dpi{120} \mathbf{cos(2\theta )=1-2sin^{2}\theta }$

$\dpi{120} \mathbf{tan(2\theta )= \frac{2tan\theta }{1-tan^{2}\theta }}$

Half angle identities :

$\dpi{120} \mathbf{sin(\frac{\theta }{2})=\pm \sqrt{\frac{1-cos\theta }{2}}}$

$\dpi{120} \mathbf{cos(\frac{\theta }{2})=\pm \sqrt{\frac{1+cos\theta }{2}}}$

$\dpi{120} \mathbf{tan(\frac{\theta }{2})= \pm \sqrt{\frac{1-cos\theta }{1+cos\theta }}=\frac{sin\theta }{1+cos\theta }=\frac{1-cos\theta }{sin\theta }}$

Product to sum identities:

2sin(x)cos(y) = sin(x+y)+sin(x-y)

2cos(x)sin(y) = sin(x+y)-sin(x-y)

2cos(x)cos(y) = cos(x+y)+cos(x-y)

2sin(x)sin(y) = cos(x-y)-cos(x+y)

Sum to product identities:

$\dpi{120} \mathbf{sinx+siny =2sin(\frac{x+y}{2})cos\left ( \frac{x-y}{2} \right )}$

$\dpi{120} \mathbf{sinx-siny =2sin(\frac{x-y}{2})cos\left ( \frac{x+y}{2} \right )}$

$\dpi{120} \mathbf{cosx+cosy=2cos\left ( \frac{x+y}{2} \right )cos\left ( \frac{x-y}{2} \right )}$

$\dpi{120} \mathbf{cosx-cosy=-2sin\left ( \frac{x+y}{2} \right )sin\left ( \frac{x-y}{2} \right )}$ OR

$\dpi{120} \mathbf{cosx-cosy=2sin\left ( \frac{x+y}{2} \right )cos\left ( \frac{y-x}{2} \right )}$

Co-function identities:

$\dpi{120} \mathbf{\mathbf{sin(\frac{\pi }{2}-\theta )=cos\theta }}$ $\dpi{120} \mathbf{\mathbf{cos(\frac{\pi }{2}-\theta )=sin\theta }}$

$\dpi{120} \mathbf{\mathbf{tan(\frac{\pi }{2}-\theta )=cot\theta }}$ $\dpi{120} \mathbf{\mathbf{cot(\frac{\pi }{2}-\theta )=tan\theta }}$

$\dpi{120} \mathbf{\mathbf{sec(\frac{\pi }{2}-\theta )=csc\theta }}$ $\dpi{120} \mathbf{\mathbf{csc(\frac{\pi }{2}-\theta )=sec\theta }}$

Geometric Sequence

August 29, 2019/by admin_ct

Archives

Degree, Radians and their conversions

Radians and degree conversion :

Convert minutes and seconds into degrees

Trigonometric Form of Complex Numbers

Multiplication and Division of Complex Numbers

Product of two complex numbers:

Quotient of Two Complex Numbers

De Moivre’s Theroem

Finding nth Roots of a Complex Number

Co terminal angles :

Coterminal angle for angle less than 360.

Co terminal angle for angles greater than 360.

Two angles are coterminal if the difference between them is a multiple of 360° or 2π.