Dot product of Vectors

/by

Dot Product of Vectors

Dot product of two vectors is also called inner product or scalar product. Dot product of two vectors u=〈u1,u2〉  and v=〈v1,v2〉  is given as,

                   u.v=〈u1,u2〉.〈v1,v2〉  = u1v1 + u2v2 

 

Example1. Use dot product to find length of vector u= 〈4,-3〉   

Solution: From property of dot product we have

\dpi{120} \mathbf{\left | u \right |= \sqrt{u.u}}

\dpi{120} \left | u \right |= \sqrt{\left \langle 4,-3 \right \rangle.\left \langle 4,-3 \right \rangle}

\dpi{120} \left | u \right |= \sqrt{4*4 +(-3)*(-3)}

\dpi{120} \left | u \right |= \sqrt{4*4 +(-3)*(-3)}

 \dpi{120} \left | u \right |= \sqrt{25} =5

 

 

Angle between two vectors:

By the definition of dot product we have,

u.v =|u||v|cosθ

\dpi{120} \mathbf{\frac{u.v}{\left | u \right |\left | v \right |} =cos\theta }

 \dpi{150} \mathbf{\theta =cos^{-1}\left ( \frac{u.v}{\left | u \right |\left | v \right |} \right )}

 

Example2. Find the angle between two vectors u=〈-4 ,-3〉  and v=〈-1,5〉

Solution:           \dpi{120} \left | u \right |=\sqrt{(-4)^{2}+(-3)^{2}}=\sqrt{25}=5

\dpi{120} \left | u \right |=\sqrt{(-1)^{2}+(5)^{2}}=\sqrt{26}

u.v = (-4,-3).(-1,5) = (-4)(-1)+(-3)(5) = -11

Angle      \dpi{120} \theta = cos^{-1}\left ( \frac{-11}{5\sqrt{26}} \right )= 115.56^{\circ}

 

Orthogonal Vectors:

The vectors u and v are orthogonal if  and only  if

u.v =0

 

Example3. Determine whether u and v are orthogonal, parallel, or neither.

a) u = 〈5,3〉  v=〈-10/4 , -3/2〉                    b) u=〈-3,4〉   v =〈20,15〉

Solution:

a) Rewriting vector v, we get

v =〈-5/2, -3/2〉  =  – 1/2〈5,3〉

v = (-1/2) u

Vector v is a scalar multiple of vector u. That shows both vectors are parallel.

 

b) Rewriting vector v

u=〈-3,4〉   v =5〈4,3〉

u.v = 〈-3,4〉 . 5〈4,3〉

= 5 (-3*4+4*3)

= 5(0) = 0

As the dot product is 0, so both vectors are orthogonal.

 

Projecting one vector onto other

Example4. Find the vector projection of u onto v. Then write u  as a sum of two orthogonal vectors, one of which is  \dpi{120} {\color{Red} proj_{v}u}.

  u =〈8,5〉   v =〈-9,-2〉

Solution:           u.v =〈8,5〉.〈-9,-2〉

= 8*-9 +5*-2 = -82

\dpi{120} \left | v\right |^{2}=\left (\sqrt{(-9)^{2}+(-2)^{2}} \right )^{2}=\left (\sqrt{85} \right )^{2}=85

Let    \dpi{120} \mathbf{u_{1}=proj_{v}u=\left ( \frac{u.v}{\left | v \right |^{2}} \right )v}

\dpi{120} =\left ( \frac{-82}{85} \right )\left \langle -9,-2 \right \rangle=\left ( \frac{82}{85} \right )\left \langle 9,2 \right \rangle

 

\dpi{120} u_{2}= u-u_{1}=\left \langle 8,5 \right \rangle-\frac{82}{85}\left \langle 9,2 \right \rangle

\dpi{120} =\left \langle \frac{-58}{85},\frac{261}{85} \right \rangle =\frac{29}{85}\left \langle -2,9 \right \rangle

 

Thus,       \dpi{120} u=u_{1}+u_{2}=\frac{82}{85}\left \langle 9,2 \right \rangle+\frac{29}{85}\left \langle -2,9 \right \rangle

 

 

 

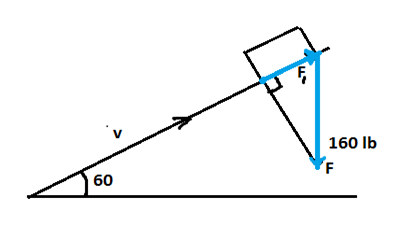
Example 5. Ojemba is sitting on a sled on the side of a hill inclined at 60° . The combined weight of Ojemba and the sled is 160 pounds. What is the magnitude of the force required for Mandisa to keep the sled from sliding down the hill?

Solution:

Since the combined weight acting downward is given 160 lb so force due to gravity is given as  F = -160j

And side of hill is represented by vector v making angle 60 with horizontal as show below.

 

v  = cos(60)i+sin(60)j

=  (1/2) i + (√3/2)  j

The force(F1 ) required to keep the sled from sliding down the hill is actually the  projection of vector F in vector v.

\dpi{120} F.v = -160j.\left \langle \frac{1}{2}i+\frac{\sqrt{3}}{2}j \right \rangle =-160*\frac{\sqrt{3}}{2}=-80\sqrt{3}

|v| = 1

\dpi{120} F_{1}=\left ( \frac{F.v}{\left | v \right |^{2}} \right )v

|F1 | = 80√3  *1 = 138.56 pounds

 

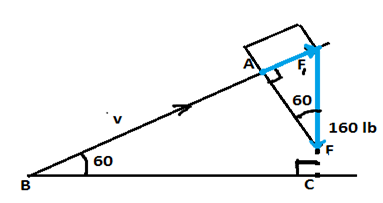
Other method:

 

Since triangles  B C  and A F  are similar triangles by AA rule, therefore   < A F1F  = <ABC = 60

Using right triangle AF1 F

\dpi{120} \frac{AF_{1}}{F_{1}F}=sin (60)

AF1=F1F * sin(60)

AF1  = 160* √3/2  = 80√3 = 138.56 pounds

 

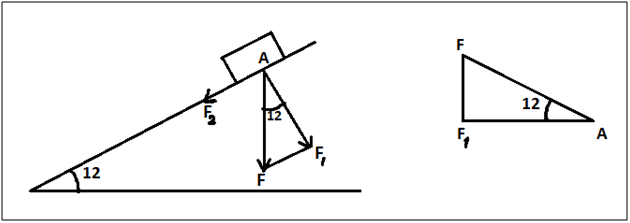
Example6. A 2000-pound car is parked on a street that makes an angle of  12°  with the horizontal (see figure).

 

(a) Find the magnitude of the force required to keep the car from rolling down the hill.

(b) Find the force perpendicular to the street.

Solution:

Weight of car 2000 pounds acting downwards is represented by vector F. This vector is resolved in two components. One F2  is acting along inclined plane  and other F1 is acting perpendicular to inclined plane .

a)  Magnitude of the force required to keep the car from rolling down the hill is given by F2 which can also be found by projection of F onto v.

Since F2   is parallel to FF1  so we find it using right triangle FF1A ,

FF1/FA     =  sin(12)

FF1    =  FA sin(12)

FF1  = 2000*sin(12) = 415.82 pounds

 

b)  Force perpendicular to street (AF1)

AF1/FA   = cos(12)

AF1 = FA cos(12)

AF1 = 2000*cos(12)

AF1  = 1956.30 pounds

 

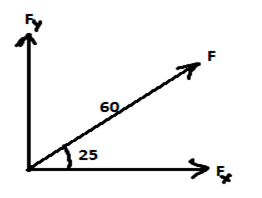
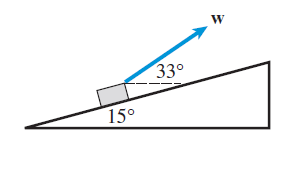
Example7. A 60-pound force F that makes an angle of 25° with an inclined plane is pulling a box up the plane. The inclined plane makes an angle 18° with the horizontal. What is the magnitude of the effective force pulling the box up the plane?

  

             

Solution:  Here effective force is parallel to inclined plane which is actually the horizontal component of force F. So we just need to find horizontal component of force.

\dpi{120} F_{x}=Fcos\theta

\dpi{120} F_{x}= 60 cos(25) =54.4 lbs

 

 

WORK :

The work done W by a constant force F acting along the line of motion of an object is given by

\dpi{150} \mathbf{W=\left | F \right |\left | \overrightarrow{AB }\right |}

If constant force F is not directed along line of motion, then work done is given by

\dpi{150} \mathbf{W=\left | F \right |\left | \overrightarrow{AB }\right |cos\theta }

 

The work done W by a constant force F as its point of application moves along the vector AB is given by either of the following.

  •  \dpi{150} \mathbf{W=\left | proj_{AB}F \right |\left | \overrightarrow{AB }\right |}         projection form
  •   \dpi{150} \mathbf{W= F . \overrightarrow{AB }}                                   dot product form

 

 

Example8. Find the work done lifting a 2600-pound car 5.5 feet.

Solution:

Since  force is acting along the line of motion (while lifting the car up to some distance) so we use formula

\dpi{120} W=\left | F \right |\left | \overrightarrow{AB }\right |

W = 2600 *5.5 = 14,300 ft pounds

 

Example9. The angle between a 75-pound force F and    \dpi{120} {\color{Red} \overrightarrow{AB}}    is 60° , where A=(-1,1) and B=(4,3). Find the work done by  F in moving an object from A to B.

Solution; Here force is not directed along line of motion but it is acting at an angle of  60°  with \dpi{120} \overrightarrow{AB}     so we use formula

\dpi{120} \overrightarrow{AB}     = (4,3)-(-1,1) = 〈5,2〉

\dpi{120} \left | \overrightarrow{AB }\right |=\sqrt{5^{2}+2^{2}}=\sqrt{29}

W = |F| |\dpi{120} \overrightarrow{AB} | cosθ

W = 75√29 cos(60)

= 75 √29(0.5)   = 201.94 ft pounds

 

 

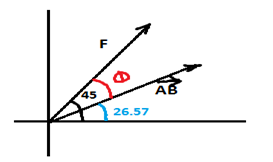
Example10.Find the work done by a force  F  of 30 pounds acting in the direction  〈2,2〉  in moving an object 3 feet from (0,0) to a point in the first quadrant along the line y = x/2 .

Solution;

We are given distance =3 ft. along the line y= (1/2)x so we can find the other point (x,y) using distance formula.

\dpi{120} D=\sqrt{(x-0)^{2}+(y-0)^{2}}

\dpi{120} 3=\sqrt{(x)^{2}+\left (\frac{x}{2} \right )^{2}}=\sqrt{\frac{5x^{2}}{4}}

\dpi{120} 3=\sqrt{5}\frac{x}{2}

x =6/√5

Y = x/2 = 3/√5    so the other point B is  (6/√5 , 3/√5 )

The force of magnitude 30 pounds acting in the direction 〈2,2〉

\dpi{120} F= 30\frac{\left \langle 2,2 \right \rangle}{\left | \left \langle 2,2 \right \rangle \right |}=30\frac{\left \langle 2,2 \right \rangle}{\sqrt{8}}

Work done

\dpi{120} W=F.\overrightarrow{AB}= 30\frac{\left \langle 2,2 \right \rangle}{\sqrt{8}}.\frac{\left \langle 6,3 \right \rangle}{\sqrt{5}}

\dpi{120} w=\frac{30}{\sqrt{40}}(12+6)= 85.38 ft. pound

 

Other way:

Given |F| =30 , |AB| = 3

Now we need to find angle between force and distance vectors.

 

Angle made by vector F

\dpi{120} tan^{-1}\left ( \frac{2}{2} \right )= 45^{\circ}

Angle made by distance vector

\dpi{120} \overrightarrow{AB}= tan^{-1}\left ( \frac{1}{2} \right )= 26.57^{\circ}

Angle between vectors F and \dpi{120} \overrightarrow{AB}

θ = 45-26.57 = 18.43°

Work done W = |F| |AB| cosθ

W = 30*3 *cos(18.43)

W = 85.38 ft pounds

 

 

 

 

Practice problems:

  1. Find the vector projection of u onto v. Then write u as a sum of two orthogonal vectors, one of which is \dpi{120} proj_{v}u.

u = 〈2,2〉      v =〈6,1〉

  1. Determine whether u and v are orthogonal, parallel, or neither.   u= 2i-2j    ,    v= -i-j
  2. Juan is sitting on a sled on the side of a hill inclined at 45°. The combined weight of Juan and the sled is 140 pounds. What force is required for Rafaela to keep the sled from sliding down the hill?
  3. Find the work done by a force F of 12 pounds acting in the direction 〈1,2〉 in moving an object 4 feet from (0,0) to (4,0).

 

 

 

 

 

 

 

 

 

 

Answers:

  1. 1/37〈84,14〉 ,  1/37〈-10,60〉
  2. orthogonal
  3. 99 pounds
  4. 21.47 ft pounds

All about Vectors in Plane

/by

Vectors in the Plane

A two dimensional vector V, is an ordered pair of real numbers, denoted in component form as <a,b>. The numbers a and b are the components of the vector v. The standard representation of the vector <a, b> is the arrow from the origin to the point (a, b) as shown below .

Here origin O is the initial point and  (a,b) is the terminal point.

Vector v is given as terminal point  minus original point.

          \dpi{120} \vec{v}    = <a, b> = (a,b)-(0,0)

 

 

Magnitude and Direction

The magnitude of v is the length of the arrow, and the direction of v is the direction in which the arrow is pointing.

If v is represented by arrow from (x1,y1 ) to (x2,y2 ) then magnitude of v is given as

\dpi{150} \mathbf{\left | v \right |=\sqrt{\left ( x_{2}-x_{1} \right )^{2}+\left ( y_{2}-y_{1} \right )^{2}}}

If v =  <a, b> then,

\dpi{150} \mathbf{\left | v \right |= \sqrt{a^{2}+b^{2}}}

The direction angle  for a vector v =  <a, b> is given as

\dpi{150} \mathbf{tan\theta =\frac{b}{a}}                            or

\dpi{150} \mathbf{\theta =tan^{-1}\left ( \frac{b}{a} \right )}

 

Example1.Using algebraic method, find magnitude and direction of given vector v = 3i-4j

Solution: Here we have the components a=3 and b=-4

Magnitude    \dpi{120} \left | v \right |= \sqrt{a^{2}+b^{2}}

\dpi{120} \left | v \right |= \sqrt{3^{2}+(-4)^{2}}=\sqrt{25}

|v| = 5

Direction angle

\dpi{120} \theta =tan^{-1}\left ( \frac{b}{a} \right )

\dpi{120} \theta =tan^{-1}\left ( \frac{4}{3} \right ) =53.13

Since given point (3,-4) lie in 4th quadrant so to find direction angle in 4th quadrant we subtract this angle from 360.

                                 θ = 360- 53.13 = 306.87°

 

 

 

 

Example2. Find     (a) u + v,     (b) u – v,    and     (c) 2u – 3v,    Then sketch the resultant vector.

     u = <2,1>  and v = <1,3>

Solution:

a) u+v = <2,1> + <1,3>

= <2+1 ,1+3> =   <3,4>

 

 

b) u-v = <2,1> – <1,3>

= <2-1 ,1-3> =     <1,-2>

 

c) 2u-3v =2<2,1>-3<1,3> = <4,2> – <3,9>

= <4-3 ,2-9> =    <1,-7>

 

 

 

 

Unit vector :

let v be any non zero vector then its unit vector ‘u’  is given as,

\dpi{150} \mathbf{u = \frac{v}{\left | v \right |}}

The vector u is called unit vector in the direction of v because its magnitude is always  unity(1).

 

Example3. Find a unit vector in the direction of given vector  v = -i-2j.  Write your answer in  

  a) component form   b)  linear combination of I and j.

Solution: First we find  magnitude of given vector v = <-1,-2>

\dpi{120} \left | v \right |= \sqrt{(-1)^{2}+(-2)^{2}}=\sqrt{5}

Unit vector

\dpi{120} u = \frac{v}{\left | v \right |}=\frac{\left \langle -1,-2 \right \rangle}{\sqrt{5}}

a)  Component form

\dpi{120} u=\left \langle \frac{-1}{\sqrt{5}},\frac{-2}{\sqrt{5}} \right \rangle

b)  Linear combination form

\dpi{120} u =\frac{-1}{\sqrt{5}}i-\frac{2}{\sqrt{5}}j

 

Resolving the vector in components

If vector v has direction angle θ,  then components of v can be found using this formula

\dpi{150} \mathbf{V=\left \langle \left | v \right |cos\theta , \left | v \right |sin\theta \right \rangle}

Where |v|cos  is called horizontal component and |v|sin  is called vertical component.

 

Example4. An airplane is flying on a bearing of 335°  at 530 mph. Find the component form of the velocity of the airplane.

Solution: Bearing is always measured from North (positive y axis)  and Direction angle is measured from positive x axis as shown in figure given below.

 

So direction angle  = 90+25=115

Horizontal component  |v|cos = 530 cos(115)

= -223.99

Vertical component |v|sin  = 530sin(115)

= 480.34

So velocity vector is given as

v = <-223.99, 480.34>

 

 

Example5. An airplane is flying on a compass heading (bearing) of  340°  at 325 mph. A wind is blowing with the bearing 320° at 40 mph.

(a) Find the component form of the velocity of the airplane.

(b) Find the actual ground speed and direction of the plane.

Solution:

Lets first sketch a diagram to represent the given situation.

 

Here AB represent velocity of airplane  which is making 110 with positive x axis. AC represent the wind velocity which is making 130 with positive x axis. AV is the resultant vector which we need to find.

a)   Resolving airplane velocity in components we get,

\dpi{120} \overrightarrow{AB}=\left \langle 325cos(110) , 325sin(110) \right \rangle =\left \langle -111.16,305.40 \right \rangle

 

b)  Resolving wind velocity in components we get,

\dpi{120} \overrightarrow{AC}=\left \langle 40cos(130) , 40sin(130) \right \rangle =\left \langle -25.71,30.64 \right \rangle

 

Resultant vector v is given as,

\dpi{120} V=\overrightarrow{AB}+\overrightarrow{AC}

V = 〈-111.16, 305.40〉 + 〈 -25.71, 30.64〉

= 〈-136.87, 336.04〉

Actual ground speed

\dpi{120} \left | v \right |= \sqrt{(-136.87)^{2}+(336.04)^{2}}

= 362.85 mph

Direction angle

\dpi{120} \theta =tan^{-1}\left ( \frac{336.04}{136.87} \right )=67.84

θ  = 180-67.84=112.16°

as the point (-136.87,336.04) lie in  2nd quadrant.

Bearing of angle 112.16°  would be  337.84°

 

 

Example6. Suppose a box is being towed up the inclined plane, as shown in the figure below. Find the force w needed in order for the component of the force parallel to the inclined plane to be 2.5 lb. Give the answer in component form.

 

Solution: Force w is making angle 33-15=18°  with the inclined plane. So w is written in component form as,

\dpi{120} w_{p}=\left \langle w cos(18),w sin(18) \right \rangle

But horizontal component parallel to inclined plane is given 2.5lb.

2.5 = w cos(18)

2.5 /cos(18)    = w

2.63 = w

 

Resultant Force making angle 33°  with horizontal is given in component form as

\dpi{120} w_{p}=\left \langle w cos(18),w sin(18) \right \rangle

 

 

Example7. Juana and Diego Gonzales, ages six and four respectively, own a strong and stubborn puppy named Corporal. It is so hard to take Corporal for a walk that they devise a scheme to use two leashes. If Juana and Diego pull with forces of 23 lb and 27 lb at the angles shown in the figure, how hard is Corporal pulling if the puppy holds the children at a  standstill?

 

Solution:

Force exerted by Juana =〈23 cos(18), 23sin(18)〉 = 〈21.87 , 7.11〉

Force exerted by Diego = 〈27cos(-15),27sin(-15)〉 = 〈26.08, -6.99〉

Total force exerted by both=〈 21.87+26.08, 7.11-6.99〉 = 〈47.95, 0.12〉

So, Corporal must be pulling with an equal force in opposite direction which is given as, 〈-47.95, -0.12〉

Magnitude of corporal force is given as

\dpi{120} \left | F \right |=\sqrt{(-47.95)^{2}+(-0.12)^{2}} =47.95 lb

 

 

Example8. A ship is heading due north at 12 mph. The current is flowing southwest at 4 mph. Find the actual bearing and speed of the ship.

Solution:

 

AN represent speed of ship due North making angle 90 with positive x axis  and AB represent speed of current to Southwest.

Southwest always makes angle 45 with horizontal axis . AV is the resultant vector which represent actual speed of ship.

Ship speed in component form = 〈12cos90 , 12sin90〉 = 〈 0, 12 〉

Current speed in component form= 〈4cos225, 4sin225〉 = 〈-2.83 ,-2.83〉

Actual (resultant) speed of ship= 〈0-2.83, 12-2.83〉 = 〈-2.83, 9.17〉

\dpi{120} \left | v\right |=\sqrt{(-2.83)^{2}+(9.17)^{2}}

|v| = 9.6mph

Direction angle of ship

\dpi{120} \theta =tan^{-1}\left ( \frac{9.17}{2.83} \right )=72.86

= 180-72.86 = 107.14°

Bearing of ship(measured from North) =342.86°

 

 

 

 

Practice problems:

  1. Forces with magnitudes of 125 newtons and 300 newtons act on a hook . The angle between the two forces is 45°. Find  the direction and magnitude of resultant of these forces.
  1. Three forces with magnitudes of 100 pounds, 50 pounds, and 80 pounds act on an object at angles of 50°, 160°and -20° respectively, with the positive -axis. Find the direction and magnitude of the resultant of these forces.
  2. loaded barge is being towed by two tugboats, and the magnitude of the resultant is 6000 pounds directed along the axis of the barge (see figure). Find the tension in the tow lines if they each make an angle of 18° with the axis of the barge.

 

 

 

 

Answers:

  1. 12.8°, 398.32N
  2.  35.65°, 113.81 lb
  3.   3154.4lb

Verify Trigonometric Identities

/by

How to verify trigonometric identities.

Trigonometric identities are those equations which are true for all those angles for which functions are defined.

The equation sinθ= cosθ is a trigonometric equation but not a trigonometric identity because it doesn’t  hold for all values of θ. There are some fundamental trigonometric identities  which are used to prove further complex identities.

We can use any of the given basic identities  or formulas to prove any identity  or evaluating  value of any  trigonometric function.

Lets look  at some examples:

Example1: prove the given identity.

\dpi{120} {\color{Red} sin^{3}x + sinx cos^{2}x =sinx}

Solution:  Solving left  side we get

\dpi{120} sinx(sin^{2}x+cos^{2}x)=sinx               [ factor out sinx]

sinx (1)  =  sinx                     [used Pythagorean identity]

sinx   =   sinx                            \dpi{120} \left [sin^{2}x+cos^{2}x=1 \right ]

 

Example2: Verify the given identity.

\dpi{120} {\color{Red} sin^{2}x-sin^{4}x=cos^{2}x-cos^{4}x}

Solution: Starting with left side,

\dpi{120} sin^{2}x-sin^{4}x=sin^{2}x\left ( 1-sin^{2}x \right )           factored out

\dpi{120} =sin^{2}x\left \left [cos^{2}x \right \right ]                 Applied Pythagorean identity

\dpi{120} =\left ( 1-cos^{2}x \right )cos^{2}x          Applied Pythagorean identity

\dpi{120} =cos^{2}x-cos^{4}x                   multiply

\dpi{120} sin^{2}x-sin^{4}x=cos^{2}x-cos^{4}x

Hence  verified the identity.

 

Example3: Verify the given identity

\dpi{120} {\color{Red} \frac{(1+sinx)}{cosx}+\frac{cosx}{1+sinx}=2secx}

Solution: Simplifying left side,

\dpi{120} \frac{(1+sinx)}{cosx}+\frac{cosx}{1+sinx}=\frac{(1+sinx)}{cosx}*\frac{1+sinx}{1+sinx}+\frac{cosx}{1+sinx}*\frac{cosx}{cosx}                                      [made the denominators same]

\dpi{120} =\frac{(1+sinx)^{2}}{cosx(1+sinx)}+\frac{cos^{2}x}{cosx(1+sinx)}

\dpi{120} =\frac{(1+sinx)^{2}+cos^{2}x)}{cosx(1+sinx)}

\dpi{120} =\frac{1+sin^{2}x+2sinx+cos^{2}x}{cosx(1+sinx)}

\dpi{120} =\frac{1+sin^{2}x+cos^{2}x+2sinx}{cosx(1+sinx)}          [rearranged the terms]

\dpi{120} =\frac{2+2sinx}{cosx(1+sinx)}

\dpi{120} =\frac{2(1+sinx)}{cosx(1+sinx)}                        [ factored out 2]

= 2/cosx     =   2secx

Hence verified the identity.

 

Example4:  Verify the following identity.

\dpi{120} {\color{Red} tan\left ( sin^{-1}\left ( \frac{x-1}{4} \right ) \right )=\frac{x-1}{\sqrt{16-(x-1)^{2}}}}

Solution:  Here we need to use trigonometric substitution.

Let  x-1= 4 sinθ               and we need to work on both sides .

Working on both sides  simultaneously ,

\dpi{120} tan\left ( sin^{-1}\left ( \frac{4sin\theta }{4} \right ) \right )=\frac{4sin\theta }{\sqrt{16-\left ( 4sin\theta \right )^{2}}}

\dpi{120} tan\left ( sin^{-1} sin\theta \right )=\frac{4sin\theta }{\sqrt{16-16sin^{2}\theta }}

 

\dpi{120} tan\theta =\frac{4sin\theta }{\sqrt{16(1-sin^{2}\theta )}}

\dpi{120} tan\theta =\frac{4sin\theta }{\sqrt{16cos^{2}\theta }}

\dpi{120} tan\theta =\frac{4sin\theta }{4cos\theta }

 

\dpi{120} tan\theta =\frac{sin\theta }{cos\theta }

tanθ         =        tanθ

Hence verified the identity.

 

Example5: Use the cofunction identities to evaluate the expression without using a calculator.

\dpi{120} {\color{Red} cos^{2}20+cos^{2}52+cos^{2}38+cos^{2}70}

Solution:

We notice that 20 and 70  are complimentary angles, same way 52 and 38 are complimentary angle.

So we can use  them  for co function identities.

\dpi{120} cos^{2}20+cos^{2}70+cos^{2}52+cos^{2}38

\dpi{120} cos^{2}20+\left (cos70 \right )^{2}+cos^{2}52+\left (cos38 \right )^{2}

\dpi{120} cos^{2}20+\left (cos(90-20) \right )^{2}+cos^{2}52+\left (cos(90-52) \right )^{2}

\dpi{120} cos^{2}20+\left (sin20 \right )^{2}+cos^{2}52+\left (sin52 \right )^{2}

\dpi{120} cos^{2}20+sin^{2}20 +cos^{2}52+sin^{2}52

\dpi{120} \left [cos^{2}20+sin^{2}20 \right ] +\left [cos^{2}52+sin^{2}52 \right ]

1       +       1  =            2

 

 

 

 

 

 

 

 

 

 

 

Practice problems:

Verify the following identities:

 

  •  \dpi{120} \frac{sec\theta -1}{1-cos\theta }= sec\theta

 

  • (1+siny)[1+sin(-y)] = cos^2(y)

 

  • \dpi{120} tan\left ( cos^{-1}\frac{x+1}{2} \right )=\frac{\sqrt{4-(x+1)^{2})}}{x+1}

 

  •  \dpi{120} tan^{2}63+ cot^{2}16-sec^{2}74-csc^{2}27                             [answer:  -2]

 

 

 

 

Solving Trigonometric equations

/by

How to solve trigonometric equations.

To solve a trigonometric equation, we use standard algebraic techniques such as collecting like terms and factoring. Our preliminary goal in solving a trigonometric equation is to isolate the trigonometric function in the equation. We can use trigonometric equations  to solve a variety of real life problems.

Lets first look at some basic equations in this video.

 

Example1: Solve  sinx +√2  = -sinx

Solution:  First we collect like terms.

sinx + sinx +√2  = 0

2sinx +√2  = 0                               [ add like terms]

sinx  = -√2/2                                        [isolate sinx ]

x  = 5π/4  ,  7π/4

First we find all possible solutions in interval [0,2π ], then we add multiples of 2π  to each of these solutions to get general form. So its general solution is given as,

\dpi{120} x=\frac{5\pi }{4}+2n\pi ,\frac{7\pi }{4}+2n\pi    where n is an integer.

 

Example2: Solve the given trigonometric equation and write all possible general solutions.

                         \dpi{120} {\color{Red} 3sec^{2}x-4=0}

Solution:

\dpi{120} 3sec^{2}x-4=0

\dpi{120} 3sec^{2}x=4

\dpi{120} sec^{2}x=\frac{4}{3}              [square root both the sides]

\dpi{120} secx=\pm \sqrt{\frac{4}{3}}

\dpi{120} \frac{1}{cosx}= \pm \frac{2}{\sqrt{3}}

\dpi{120} cosx = \pm \frac{\sqrt{3}}{2}

Since cos has a period of [0, 2π]  so we find all the solutions in this interval ,taking into account both positive and negative signs. So we get,

x =π/6 , 5 π/6  , 7π/6 , 11π/6

General solution is given as,

\dpi{120} x=\frac{\pi }{6}+2n\pi , \frac{5\pi }{6}+2n\pi , \frac{7\pi }{6}+2n\pi , \frac{11\pi }{6}+2n\pi

Where n is an integer.

 

Solving trigonometric equations given in quadratic form.

Some trigonometric equations are given in quadratic form or they are given in such form which can be converted to quadratic form. Such equations can be solved using factoring by different ways as shown in these following examples.

Example: Find all solutions of the equation in the interval [0,2π]. 

{\color{Red} 2cos^2(x)-5cosx+2=0}

Solution:

As this equation is quadratic in nature  so we use factoring to get its factors.

To make factoring process easy, we can assume cosx  as y and get the factors of

\dpi{120} 2y^{2}-5y+2 =0

(2y-1)(y-2) = 0

Plug in back y and we can get the factors as,

(2cosx-1)(cosx-2) = 0

2cosx -1 = 0                          cosx -2 = 0

Cosx = 1/2                                cosx = 2 [no solution]

Note: Here no solution possible for cosx =2 as 2 lie outside the range of cosine function.

So its solution in the given interval  is,

cosx =\frac{1}{2}

x=\frac{\pi }{3}, \frac{5\pi }{3}

 

Example : Solve the given trigonometric equation and find  its general solutions.

{\color{Red} tan^4(\theta )-13tan^2(\theta )+36 =0}

Example3: Solve the given trigonometric equation and write all possible general solutions.

\dpi{120} {\color{Red} cos^{3}x=cosx}

Solution:

\dpi{120} cos^{3}x=cosx

\dpi{120} cos^{3}x-cosx=0

\dpi{120} cosx \left (cos^{2}x-1 \right )=0                   [factored out cosx]

set each factor =0 and solve for x,

cosx =0                                           \dpi{120} cos^{2}x-1=0

x = π/2 , 3π/2                                \dpi{120} cosx=\pm 1

x = π/2 , 3π/2                                       x = 0, π

These are the solutions  in the interval  [0,2π]

To get general solutions we add 2nπ to each primary solution.

x=π/2+2nπ , 3π/2+2nπ ,0+2nπ, π+2nπ

π/2+2nπ , 3π/2+2nπ can be combined to get π/2+nπ  and hence general solutions are given as,

x =  π/2+nπ , 2nπ  , π+2nπ   ,     n∈Z

 

 

Solving trigonometric equations by squaring both sides.

Sometimes we are not able to solve trigonometric equations either by factoring or using any identity. In such case we can try squaring both sides and then solving it further as shown in following examples.

Example: Find all solutions of the equation in the interval [0,2π]

cscx + cotx = 1

Solution:  In such cases we square both sides  and solve .

\dpi{120} \left ( cscx \right )^{2}=\left ( 1-cotx \right )^{2}

\dpi{120} csc^{2}x= 1-2cotx +cot^{2}x

\dpi{120} csc^{2}x-cot^{2}x=1-2cotx

1= 1-2cotx

0=-2cotx

0= cotx

\frac{\pi }{2}= x

 

Example : Solve the given trigonometric equation and write its general solutions. Also check extreneous solutions.

{\color{Red} sin(\theta )-1=cos(\theta )}

 

 

Solving multiple angle trigonometric equations.

Example: Solve the multiple angle equation and write its general solution.

\dpi{120} {\color{Red} cos\left ( \frac{x}{2} \right )=\frac{\sqrt{2}}{2}}

Solution:

\dpi{120} cos\left ( \frac{x}{2} \right )=\frac{\sqrt{2}}{2}

\dpi{120} \frac{x}{2}= \frac{\pi }{4}, \frac{7\pi }{4}                      [cos being positive in  1st and 4th quadrants]

This is the solution in the interval [0,2π]  as cos has a period of 2π.

Its general solution would be given as,

\dpi{120} \frac{x}{2}=\frac{\pi }{4}+2n\pi , \frac{7\pi }{4}+2n\pi

Multiplying  both sides by 2 to Isolate  x we get,

\dpi{120} x=\frac{\pi }{2}+4n\pi , \frac{7\pi }{2}+4n\pi , n\in Z

 

 

 

 

Practice problems:

Solve the given trigonometric equation and write all possible general solutions.

  • \dpi{120} cotx cos^{2}x =2cotx
  • \dpi{120} 2sec^{2}x +tan^{2}x-3=0
  • Sin(2x) = -√3/2
  • \dpi{120} 2sin^{2}x +3cosx-3 =0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answers:

  • \dpi{120} x=\frac{\pi }{2}+n\pi
  • \dpi{120} x=\frac{\pi }{6}+2n\pi ,\frac{5\pi }{6}+2n\pi ,\frac{7\pi }{6}+2n\pi ,\frac{11\pi }{6}+2n\pi
  • \dpi{120} x=\frac{2\pi }{3}+n\pi , \frac{5\pi }{6}+n\pi
  • \dpi{120} x=2n\pi ,\frac{\pi }{3}+2n\pi ,\frac{5\pi }{3}+2n\pi

Where n is an integer.

 

SOHCAHTOA rule and word problems.

/by

SOHCAHTOA rule and word problems.

Trigonometry is all about triangles and it has numerous applications in science and engineering.

Lets learn about some terms related with right triangle.

 

Opposite side: The side which is opposite to angle θ

Adjacent side: The side on which angle θ is based.

Hypotenuse:  The longest side and opposite to 90°  angle.

Basic three functions of trigonometry are Sine, Cosine and Tangent. These are just the ratios of sides of right triangle.  That’s why these are also called trigonometric  ratios and in short they are abbreviated as sin, cos and tan.

Fundamental trigonometric identities:

  • sinθ =1/cscθ     or    cosecθ  = 1/sinθ
  • cosθ=1/secθ      or    sec  = 1/cosθ
  • tanθ = 1/cotθ    or   cotθ  =1/tanθ
  • tanθ =sinθ/cosθ    or   cot  =cosθ/sinθ

Pythagorean identities:

  • \dpi{120} \mathbf{sin^{2}\theta +cos^{2}\theta =1}
  • \dpi{120} \mathbf{1+tan^{2}\theta =sec^{2}\theta }
  • \dpi{120} \mathbf{1+cot^{2}\theta =csc^{2}\theta }

 

Example: Using given right triangle find all six trigonometric  function of θ.

 

Solution:  First, we find hypotenuse using Pythagorean identity.

\dpi{120} \mathbf{\left ( hyp \right )^{2}= \left ( adj \right )^{2}+\left ( opp \right )^{2}}

\dpi{120} \left ( hyp \right )^{2}= \left ( 4 \right )^{2}+\left ( 3 \right )^{2}

\dpi{120} \left ( hyp \right )^{2}= 16+9=25

hyp = 5

Using  SOHCAHTOA  rule, we get

Sinθ = O/H= 3/5                                 Cosecθ =H/O= 5/3

Cosθ = A/H= 4/5                                 Secθ = H/A = 5/4

Tanθ =O/A = 3/4                                 Cotθ = A/O =4/3

 

Example: Find each angle measure to nearest degree.

   a)tanA = 0.6249                        b) sinX = 0.4540

Solution:  To  solve these type of problems we need calculator. Since these use  inverse functions so we need to be familiar with inverse trigonometric buttons on our calculator.

a)             tanA = 0.6249

\dpi{120} A= tan^{-1}(0.6249)

Enter 0.6249 in your calculator  and press  arctan \dpi{120} \left ( tan^{-1} \right )  button

We get,          A = 32.001

Which when rounded to nearest degree become 32°

If your calculator doesn’t have  inverse trigonometric functions  then press inverse(INV) button after entering the number and inverse functions will appear .

b)            sinx = 0.4540

\dpi{120} x=sin^{-1}(0.4540)

x = 27.0006  ≈  27°

 

Example: Find the missing side of given right triangle round to nearest tenth.

 

Solution:  Given Adjacent side(A) =x

Hypotenuse (H)= 17

Angle(θ ) = 30

We know that ,            Cosθ = A/H

Cos(30)  =  x/17

17 cos(30) = x

14.7   = x

 

Example: A wheelchair ramp is 4.2 m long. It rises 0.7 m. What is its angle of inclination to the nearest degree?

Solution: Lets  make a picture to understand  this problem better. Ramp makes the hypotenuse and rise of 0.7 make opposite side for right triangle.

 

Here we need to find angle θ.

We know that,  sinθ   = O/H

sinθ   = 0.7 /4.2

\dpi{120} \theta =sin^{-1}\left ( \frac{0.7}{4.2} \right )

θ  = 9.59 ≈ 10°

 

Example: The angle of elevation of the sun is 68° when a tree casts a shadow 14.3 m long. How tall is the tree, to the nearest tenth of a meter?

 

Solution:  Here opposite(vertical) side form the height of tree and adjacent(horizontal) side form the shadow of tree and angle  of elevation is given 68 degrees.

 

We know that                    tanθ= O/A

tan(68) = x/14.3

14.3*tan(68) =x

35.393  =   x

35.4 m  =  x

 

 

 

 

 

Practice problems:

  • Find all the six trigonometric functions of  θ for a given right triangle with hypotenuse as 41 and opposite side as 9.
  • An airplane is flying at an altitude of 6000 m over the ocean directly toward a coastline. At a certain time, the angle of depression to the coastline from the airplane is 14°. How much farther (to the nearest kilometer) does the airplane have to fly before it is directly above the coastline?
  • A 9.0 m ladder rests against the side of a wall. The bottom of the ladder is 1.5 m from the base of the wall. Determine the measure of the angle between the ladder and the ground, to the nearest degree.
  • A person flying a kite has released 176 m of string. The string makes an angle of 27° with the ground. How high is the kite? How far away is the kite horizontally? Answer to the nearest meter.

 

 

 

 

 

Answers:

  • Sin=9/41 , cos=40/41 ,tan=9/40 , csc=41/9 , Sec=41/40 ,cot =40/9
  • 24 km
  • 80°
  • 80 m high, 157 m away

 

Graphing Sine and Cosine functions ( vertical & Horizontal Translation)

/by

Sine and Cosine Functions

Horizontal Translation:

In the standard equation y=asin(bx-c)+d , constant c creates the horizontal translation of basic sine and cosine curves. Comparing y= aSin(bx) with y= aSin(bx-c) , we find that graph of y= aSin(bx-c) completes one cycle from bx-c=0  to bx-c =2π .  By solving for x, we can find the interval for new cycle as,

Function                     left end point                     Right end point

Y= aSin(x)                     x=0                                       x =2π

Y= aSin(bx)                   x=0                                        x=2π/b

Y= asin(bx-c)               x = c/b                                   x = c/b  + 2π/b         

We see that period interval  of old sine function y= aSin(bx)  is [0,2π/b] whereas the period interval for new horizontally translated function would be   \dpi{120} \left [ \frac{c}{b},\frac{c}{b}+\frac{2\pi }{b} \right ]

 

 

This implies that the period of y=aSin(bx-c) is  2π/b  and the graph is shifted by an amount c/b. The number c/b is the phase shift.

 

 

Example1. Find amplitude ,period and phase shift for the following function and analyze its graph in terms of horizontal translation.

  Y= 2Sin(x – π/3)

Solution: Comparing this equation with standard equation

y= aSin(bx-c) we get,

Amplitude(a) = 2

b=1  =>  period =2π/b  =2π/1  = 2π

Phase shift =c/b  = π/3  (right)

By solving the equations,

\dpi{120} x-\frac{\pi }{3}=0 \Rightarrow x=\frac{\pi }{3}

\dpi{120} x-\frac{\pi }{3}=2\pi \Rightarrow x=\frac{\pi }{3}+2\pi =\frac{7\pi }{3}

So we get new interval for one cycle as  \dpi{120} \left [ \frac{\pi }{3},\frac{7\pi }{3} \right ] . That means complete cycle of interval [0,2π ] of  y= 2sinx get shifted to right by π/3 . Now we get its 5 key points by dividing interval \dpi{120} \left [ \frac{\pi }{3},\frac{7\pi }{3} \right ]  into 4 equal parts and they are,

Intercept             max.             intercept                     min.                       intercept

   (π/3,0)          (5π/6,  2)        (4π/3 ,0)               (11π/6 ,-2)                 (7π/3 ,0)

By connecting these points we get the following graph.

 

 

Example2. . Find amplitude ,period ,phase shift  and frequency  for the following function and analyze its graph in terms of horizontal translation.

                      Y= -3cos(2πx+4π)

Solution: Comparing it with standard equation y= aCos(bx-c) we get,               Amplitude(a)= 3

b = 2π    =>   period =2π/b  =2π/2π  = 1

Phase shift =c/b  =-4π/2π  = -2 (left)

Frequency(f) =b/2π  = 1/2π

Solving the equations,

2π x+4π  = 0

2πx = -4π

x =-4π/2π  = -2(left end point)

2π x+4π  = 2π

2π x = -2π

x =-2π/2π  = -1 (right end point)

So we get the interval [-2,-1] for  one cycle of graph. Now we divide this interval into equal 4 parts to get  key points.

Intercept             max.            intercept                 min.                        intercept

   (π/3 ,0)          (5π/6 ,2)        (4π/3,0)               (11π/6,-2)                 (7π/3,0)

Connecting these points we get following graph.

 

Vertical Translation:

This type of transformation is caused by constant d in the equation  y=asin(bx-c)+d.

Graph get shifted up by d units for d>0 and it get shifted down by d units for d<0.

In other words, graph oscillates about the horizontal line y=d instead of  x axis.

 

Example: Sketch the graph of y=2+3cos2x. Also find its amplitude, period ,phase shift, vertical shift  and equation of new central axis.

Solution: Comparing it with standard cosine equation

y= aCos(bx-c)+d we get,

Amplitude(a) = 3

b =2   =>   period =2π/b   = 2π/2  = π

c =0   =>  Phase shift =c/b  =0/b  = 0

d= 2  =>   vertical shift = 2 units up

Equation of new central axis  y= 2

Vertical translation has  the effect on y coordinates  which get increased or decreased  depending on value of d. Here we have the period interval [0,π ].  We divide this interval into 4 equal parts to get key points and they are:

Intercept             max.                  intercept               min.                    intercept

   (0,5)                   (π/4,2)               (π/2,-1)               (3π/4,2)                 (π,5)

Connecting all these points , we get the following graph.

 

 

 

 

 

 

 

 

Practice problems:

Describe the relationship between graphs of f and g  and graph them on same set of axis.

  1. f(x) = sin(2x)

g(x) = 3 +sin(2x)

2.  f(x) = sin(4x)

g(x) = sin(4x+π) +2

3. g(x) is related to a parent function f(x)= sinx or f(x)= cosx

Describe the sequence of transformations from f(x) to g(x)  and sketch the graph of g(x)

g(x)= 2sin(4x-π )-3

g(x) = cos(x-π ) +2

 

 

 

Graphing Sine and Cosine functions(stretching & shrinking)

/by

Sine and Cosine functions (Stretching&Shrinking)

Sinx and cosx are the two basic and frequently used trigonometric functions. Their graphs have same properties. Lets have a look at these properties.

  • Domain of both sinx and cosx is all real numbers (-∞ , ∞).
  • Range of each function is [-1,1].
  • Amplitude of each of these functions is 1.
  • Each of them has same period of 2π . (Period is the length of one complete cycle here).
  • Maximum and minimum values of both functions are 1 and -1 respectively but they occur at different points for each of these functions

 

Important terms related with graphs of trigonometric functions:

  • Amplitude: It is the distance between central line and peak of the graph. Or it is the height from central line  to either maximum  or minimum point. Amplitude(a) is half the distance between maximum  and minimum points.

\dpi{120} \mathbf{|a|=\frac{y_{max}-y_{min}}{2}}

  • Period: It is the time in which one cycle is completed. Horizontal length of each cycle is called period. For a function y=asin(bx) or acos(bx) , period is given by the formula,

  period=2π/b

  • Phase shift: Phase shift is how far a graph is shifted horizontally from its usual position. It is denoted by c so positive  c means  shift to left and negative c means shift to right.
  • Vertical shift: This is how far a graph is shifted up or down from its usual position. It is denoted by d so +d means shifted up and –d means shifted down.
  • Frequency: it is the number of cycles completed in one second. It is the reciprocal of period so its formula is given as

   freq(f) =b/2π 

Putting all the above terms together, we get the following equation.

Y= asin(b(x-c))+d                                    OR

y= acos(b(x-c))+d                 

 

Using key points to sketch a curve:

To sketch the basic sine and cosine functions by hand it helps to note five key points  in one period. These key points are : intercepts, maximum and minimum points.

 

 

Example: Sketch the following function using five key points on the interval [-π , 4π]

                             Y = 2sinx

Solution: When we compare it with y= asin(b(x-c))+d, we see that there is no phase shift and vertical shift (c=0,d=0).

Here we have amplitude ,  a=2

Using   b=1  ,   period = 2π/b  =2π/1  = 2

Now we divide this period of 2π  into 4 parts  to get key points.

Initial point of sinx curve is (0,0) which is also x intercept.

Intercept                max.                 intercept                    min.                           intercept

   (0,0)                     (π/2 ,2)              ( π,0)                        (3π/2 ,-2)                      ( 2π,0)

After connecting all these five points we get a smooth curve. Extending  this curve in both directions over the interval  [-π , 4π ] we get the graph as shown below. Graph of 2sinx  is same as sinx, except amplitude get doubled.

 

 

Here is a summary of vertical and horizontal shrink and stretch and their effects on amplitude and period.

 

 

Function Transformation Effected para-meters              Graphs
\dpi{120} \mathbf{y=asinx , a>0} Vertical stretch Amplitude get increased
\dpi{120} \mathbf{y=\frac{1}{a}Sinx}

a>0

 Vertical shrink Amplitude get reduced
\dpi{120} \mathbf{y=acos(bx)}

a>0, b>0

 Horizontal shrink Period get decreased
\dpi{120} \mathbf{y=acos\left ( \frac{x}{b} \right )}

a>0, b>0

 Horizontal stretch Period get increased
\dpi{120} \mathbf{y=-asin(x)}

a>0

 Reflection across x axis Max. and min. get  reversed

 

Example2. Sketch the graph of y= sin(x/2).Compare it  with the graph of basic function y=sinx. How its parameters amplitude and period get effected?

Solution: Comparing the given equation y= sin(x/2) with standard basic sin function y= aSin(bx), we get

Amplitude(a) = 1   and  b =1/2

\dpi{120} period= \frac{2\pi }{b}=\frac{2\pi }{\frac{1}{2}}= 4\pi

So this function has period interval [0, 4π ] as compared to the basic period interval of [0, 2π ]. Now we divide this interval into 4 equal parts with values π, 2π , 3π  to get five key points.

Intercept             max.           intercept             min.             intercept

   (0,0)                  (π,1)             ( 2π,0)                (3π,-1)              (4π ,0)

Connecting all these points , we get the following graph.

 

We can observe that there is no effect on amplitude  but period get doubled. So there is horizontal stretch.

Same way we can draw the graphs for functions like y=sin(2x)  where period get reduced by half so new period  would be [0,π ]. Then we divide this period into 4 equal parts and get a graph which is compressed horizontally .

For the function y= aSinx  or Y= aCosx  its amplitude get increased  by factor ‘a’  so there would be vertical stretch and for the function  y= (1/a) Sinx amplitude get decreased by  factor ‘a’ causing vertical shrink. X coordinates of 5 key points will remain same as period remain unaffected but y coordinates changed to –a and a accordingly.

 

 

 

 

Practice problems:

  • Find period and amplitude for the following functions and then graph them using five key points.
  1. Y= Cos(2x)
  2. Y=-4Sin(x)
  3. Y= Sin(x/3 )
  4. Y=(1/4) Cos(x)

 

 

 

 

 

 

 

Answers:

amp.= 1 , period =[0 π]

amp.= 4 ,period =[0,2π ]

amp. =1 ,period= [0,6π ]

amp. = 0.25 , period= [0,2π]

 

Reference Angle

/by

Reference angle: 

Let  θ be an angle in standard position. Its reference angle θ’ is the acute angle  formed by the terminal side of  θ and the horizontal axis.

 

The values of the trigonometric functions of angles greater than (or less than ) can be determined from their values at corresponding acute angles called reference angles.

 

Below are the rules to find reference angles of θ in quadrants II , III and IV .

 

            Quadrants                            Formula

  Radians                                   Degrees
                 II       π-θ                                        180-θ
                III        θ-π                                       θ-180
                 IV      2π-θ                                       360-π

 

 

 

 

Lets look at this video lesson :

 

 

Example: Find reference angle θ’ of  each of the following angles.

      a)315°                       b) -150°                        c) 1.8°

Solution:  a) 315°

Since it lie in 4th  quadrant  so we  use  rule  θ’=360-θ

Reference angle  is θ’=360-315 = 45°

b) -150°

First we find positive  coterminal angle of  -150

Positive coterminal angle = -150+360= 210

Since 210 lie in 3rd  quadrant  so we  use  rule θ’ = θ – 180

Reference angle  is θ’ = 210-180 =30°

c) 1.8

This angle is given in radians and it lie in 2nd quadrant .

Considering  π= 3.14

π/2   = 3.14/2  =1.57

1.8 lie between 1.57 and 3.14  which is 2nd quadrant (π/2<θ<π )

For 2nd quadrant  we use θ’ = π-θ

= 3.14-1.8 = 1.34 radians

 

 

 

Practice problems:   

Find reference angle of  each of the following angles.

  • 57°
  • -210°
  • 1.2
  • 11π/6
  • 3.5

 

 

 

 

 

 

 

Answers:

  • 57°
  • 30°
  • 1.2 radians
  • π/6
  • 0.36 radians

Law of Sines and its Applications

/by

Law of Sines and its Applications

Law of Sines is used to solve oblique triangles. Oblique triangles are the triangles which have no right angles. As standard notation for law of Sines and Cosines , the angles of a triangle are labeled  as A,B and C and their opposite sides are labeled as a, b and c as shown in figure given below.

 

Law of Sines is used to solve the oblique triangle in any of the following two cases.

  1. Two angles and any side.
  2. Two sides and an angle opposite to one of them.

 

Law of Sines can also be written in reciprocal form.

 

\dpi{150} \mathbf{\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}}

 

 

Example1. Because of prevailing winds, a tree grew so that it was leaning 4° from the vertical. At a point 40 meters from the tree, the angle of elevation to the top of the tree is 30°  . Find the height  h of the tree.

 

Solution: lets first get a geometrical diagram to represent the given situation.

 

Here we have <A=90+4=94, <B=30 , therefore using angle sum property of triangles we get,

C = 180-(94+30)= 56

Side c opposite to angle C is given 40m and  side b which is height of tree, is to be found.

By law of Sines we have,

\dpi{120} \frac{b}{sinB}=\frac{c}{sinC}

\dpi{120} \frac{h}{sin30}=\frac{40}{sin56}

h  = (40/sin56)*sin(30) =24.12m

Therefore height of tree is 24.12m

 

 The Ambiguous case (SSA)

If two sides and one opposite angle are given then three possible  situations can occur.

  • No such triangle exist (no solution)
  • One such triangle exist(one solution)
  • Two distinct triangle exist (two solutions)

 

No solution case

Example2: show that there is no such triangle for which a=15, b=25 and  A=85° .

Solution: Using law of Sines,

\dpi{120} \frac{sinB}{b}=\frac{sinA}{a}

SinB = b* (sinA/a)

SinB = 25*(sin85/15)

SinB = 1.660 > 1

Which is not possible because Sin ranges from -1 to 1, so no triangle is possible with these sides.

 

One solution case

Example3:For a given triangle ABC, given that a=22inches, b= 12inches  and <A=42° . Find remaining side and angles.

Solution: By the law of Sines,

\dpi{120} \frac{sinB}{b}=\frac{sinA}{a}

sinB    = b*(sinA/a)

sinB = 12*(sin42/22)

\dpi{120} B= sin^{-1}(0.36498)= 21.4^{\circ}

Now we can find third angle easily, using angle sum property of triangles.

<C = 180-(42+21.4) = 116.6°

Using two angles  and one side we can find third side,

\dpi{120} \frac{b}{sinB}=\frac{c}{sinC}

\dpi{120} \frac{12}{sin21.4}=\frac{c}{sin116.6}

\dpi{120} \frac{12}{sin21.4}*sin116.6 =c

 

29.40 = c

 

Two solutions case

Example4. Find two triangles for which a=12m, b=31m and <A=20.5°

Solution: By the law of Sines,

\dpi{120} \frac{sinB}{b}=\frac{sinA}{a}

\dpi{120} \frac{sinB}{31}=\frac{sin20.5}{12}

\dpi{120} sinB=31*\frac{sin20.5}{12}=0.9047

\dpi{120} B= sin^{-1}(0.9047)

There are two angles B1= 64.8°  and B2=(180-64.8)=115.2°   ,

So there are two possible triangle solutions.

For B1=64.8° , we get <C = 180-(20.5+64.8) = 94.7°

\dpi{120} \frac{c}{sinC}=\frac{a}{sinA}

\dpi{120} \frac{c}{sin94.7}=\frac{12}{sin20.5}

c = (12/sin20.5)*sin(94.7)

c = 34.15m

For B2 =115.2°  , we get C =180-(20.5+115.2)= 44.3°

\dpi{120} \frac{c}{sin44.3}=\frac{12}{sin20.5}

c  = (12/sin20.5)*sin(44.3)

c  = 23.93m

 

 

Area of Oblique Triangle :

The area of any triangle is one half  the product of two sides times the sine of their included angle.

\dpi{150} \mathbf{A=\frac{1}{2}bcsinA =\frac{1}{2}abainC=\frac{1}{2}acsinB}

 

Example5. Find the area of  triangle having  angle and sides as,

          A=43° 45’ , b=57 and c=85

Solution: First we convert the angle from degree and minutes to decimal degrees so that we can calculate sine of angle using calculator.

43°45’ = 43 + 45/60  = 43.75°

\dpi{120} Area A=\frac{1}{2}bcsinA

\dpi{120} A=\frac{1}{2}(57)(85)sin(43.75) =1675.2

A = 1675.2  sq. units

 

 

Example6. A boat is sailing due east parallel to the shoreline at a speed of 10 miles per hour. At a given time, the bearing to the lighthouse is S70°E, and 15 minutes later the bearing is S63°E. The lighthouse is located at the shoreline. What is the distance from the boat to the shoreline?

 

Solution: First we draw the  given situation as geometric diagram as under,

 

Here A,B are the two different position of boat and C is the shoreline. CD is the perpendicular distance from boat to shoreline.

To find the distance between two positions of boat A and B  we use distance =speed*time formula.

Distance AB = 10mph *(15/60)hrs

= 10*  = 2.5 miles

Angle B= 90+63 = 153°

Using law of Sines,

\dpi{120} \frac{x}{sin20}= \frac{2.5}{sin7}

x  = (2.5/sin7) *sin20

x = 7.016 miles

To find perpendicular distance between boat and shoreline we use right triangle BCD.

y/7.016  = sin(27)

y = (7.016)sin(27)

y = 3.2 miles

So the distance from boat to shoreline is 3.2 miles.

 

 

 

Practice problems:

  1. Use the Law of Sines to solve the triangle. If two solutions exist, find both. Round your answers to two decimal place.

A=58° ,  a=11.4,  b=12.8

  1. Find the area of triangle having angle and sides as ,

B =72°30′  a=105, c=64

  1. The angles of elevation to an airplane from two points A and B on level ground are 55° and 72° The points  A and B  are 2.2 miles apart, and the airplane is east of both points in the same vertical plane. Find the altitude of the plane.
  2. A bridge is to be built across a small lake from a gazebo to a dock . The bearing from the gazebo to the dock is S41°W From a tree 100 meters from the gazebo, the bearings to the gazebo and the dock are S74°E and S28° E respectively. Find the distance from the gazebo to the dock.

 

 

 

 

 

 

 

Answers:

1.Two solutions:  B=72.21°, C=49.79° , c=10.27

B=107.79°, C=14.21° , c=3.30

  1. 3204.5 sq. units
  2. 5.86 miles
  3. 77m

 

 

 

 

 

Graphs of other Trigonometric functions (tanx , cotx, secx, cscx)

/by

Graphs of other Trigonometric functions

(tanx , cotx, secx, cscx)

Tan(-x)= -Tanx

Tan(x) being an odd function is symmetric with respect to origin.

We know from the identity  tanx = sinx/cosx

So tanx  is undefined where cosx is 0. We know that cos is 0 at each odd multiple of π/2. Tanx will have vertical asymptotes where cosx  is 0 so tanx  has vertical asymptotes at each odd multiple of π/2. Also period of tan(x) is π so vertical asymptotes  are

\dpi{120} x= \frac{\pi }{2}+ n \pi

where n is an integer.

 

Sketching  the graph of tangent functions y= atan(bx-c)is similar to sketching the graph of  y=asin(bx-c) where we locate key points , vertical asymptotes and x intercepts. Two consecutive asymptotes are found  by solving equations,

bx-c = -π/2                                         bx-c = π/2

Similarly cotx = cosx/sinx  so this would be undefined  where sinx is 0. As sinx is 0 at each multiple of  π so cotx has vertical asymptotes  at nπ  where n is an integer.

Two consecutive vertical asymptotes of the graph of

y= acot(bx-c)

can be found by solving the equations bx-c=0 and bx-c =π .

Here is a summary of all properties of tan and cot functions.

            tan(x)             cot(x)
Domain   \dpi{120} x\neq (2n+1)\frac{\pi }{2}, x\in R      \dpi{120} x\neq n\pi , x\in R
Range          (-∞,∞)           (-∞ ,∞)
Vertical asymptotes        \dpi{120} x=(2n+1)\frac{\pi }{2}        x = nπ
Period                   π              π
Symmetry Symmetric with respect to origin Symmetric with respect to origin

 

Mid point between two vertical asymptotes is the x intercept. After plotting  vertical asymptotes and x intercept we find one additional point between each asymptote and x intercept to know the direction of graph. Amplitude of tangent,cotangent functions is not defined. Lets work on some examples to understand this graphing.

 

 

Example 1. Find vertical asymptotes and x intercepts of y=-3tan(2x)  and graph one complete cycle.

Solution: By solving the equations,

2x = – π/2               and                     2x = π/2

x = – π/4                                               x =π/4

We see that two consecutive vertical asymptotes occur at -π/4   and  π/4. Between these two points we find mid point  which is x intercept  and one point each between asymptote and x intercept as shown in table.

x    -π/4    -π/8       0     π/8    π/4
Y=-3tan(2x) Undef.      3       0     -3 Undef.

 

We observe that graph of y=-3tan(2x) decrease between each consecutive vertical asymptotes because here amplitude a(-3)<0.In other words graph for a<0 is a reflection in the x axis of graph for a>0.

 

Example2. Find vertical asymptotes and x intercepts of  y=2cot(x/3)  and graph one complete cycle.

Solution: By solving equations,

x/3 = 0                     and                    x/3 = π

x = 0                                                   x = 3π

We get vertical asymptotes at x=0 and 3π . Here period is 3π  which is the distance between consecutive asymptotes. Between these two vertical asymptotes we plot x intercept and other points between each asymptote and x intercept as shown in table.

x     0    3π/4      3π/2     9π/4     3π
Y=2cot(x/3) Undef.      2       0     -2 Undef.

 

 

 

 

Graphs of reciprocal functions(Secant and Cosecant) :

 

Graphs of Secant and Cosecant can be obtained from sine and cosine using  reciprocal identities.

Sec x = 1/cosx                                    Cosec x = 1/sinx

Y coordinate of sec x is the reciprocal of y coordinate of cosx, same way, y coordinate of cosec x is the reciprocal of y coordinate of sin x for same values of x. But reciprocals doesn’t exist  when sinx and cosx are 0.

The graph of secx has vertical asymptotes at x= π/2+ nπ  and  cosec x has vertical asymptotes at x= nπ where n is an integer.

Here is a summary of all the properties of both reciprocal functions.

            Csc(x)             Sec(x)
Domain       \dpi{120} x\neq n\pi , x\in R     \dpi{120} x\neq (2n+1)\frac{\pi }{2}, x\in R
Range        (-∞ ,-1]U[1,∞ )     (-∞ ,-1]U[1,∞ )
Vertical asymptotes        X = nπ       \dpi{120} x=(2n+1)\frac{\pi }{2}
Period                   2π                   2π
Symmetry Symmetric with respect to origin. Symmetric with respect to y axis.

 

To sketch the graph of Sec x and Cscx we draw a table of x,y values where y values are just the reciprocals  of y values of cosx and sinx except at vertical asymptotes. Maximum value of sinx becomes the minimum value of cscx and minimum value become the maximum value between each vertical asymptotes. All x intercepts of sinx and cosx changes to vertical asymptotes of  cscx and secx.

Lets work on a few examples to understand its working better.

 

Example3. Find the vertical asymptotes and sketch the graph of

                             Y= 2Csc(x+π/4 )

Solution:           Y= 2Csc(x+π/4 )

\dpi{120} y =\frac{2}{sin\left ( x+\frac{\pi }{4} \right )}

By solving the equations,

x+π/4  = 0                          and              x+π/4  = π

x = -π/4                                                     x = π-π/4  = 3π/4

we get vertical asymptotes as   \dpi{120} x=-\frac{\pi }{4},\frac{3\pi }{4},\frac{7\pi }{4}   etc.

which are the zeros of sin(x+π/4) . Divide the space between two vertical asymptotes using five key points and get following table of values. We get values of 2sin(x+π/4)  as well as 2Csc(x+π/4 ) to understand  how they are related with each other.

      x  -π/4    0  π/4  π/2  3π/4  π  5π/4  3π/2  7π/4
2sin(x+π/4 )  0  √2   2  √2   0  -√2  -2  –√2   0
2Csc(x+π/4 ) V.A.  2√2   2  2√2 V.A.  -2√2  -2  -2√2 V.A.

 

Plotting these points of both functions on same grid we get the following graph.

 

 

 

Practice problems:

  1. Sketch the graph of the following functions. Include two full periods.

Y = tan(4x)

Y = 2cot(x+π/2 )

Y = 2Csc(x-π)

Y = sec(3x)

 

 

Check : Draw these graphs manually using the process as explained above and then check them using graphing calculator. You can use many graphing tools available online.