Subtopic Archive - Page 8 of 10

Pascal’s Triangle and Binomial Theorem

August 22, 2019/by admin_ct

An algebraic expression containing two terms is called binomial expression. The general form of the binomial expression is (x+a) and the expansion of $\mathbf{(x+a)^{n}}$ , where n is a natural number, is called binomial theorem. It gives a formula for the expansion of the powers of binomial expression.

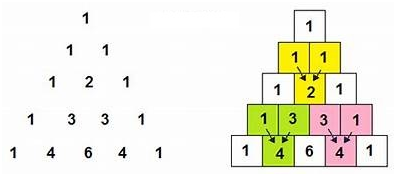
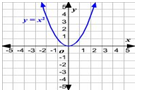
The coefficients in the binomial expansion follow a specific pattern known as Pascal’s triangle.

Following are some important features of Pascal’s triangle.

–Each row is bounded by 1 on both sides.

-Any entry except first and last, is the sum of two entries in preceding row , one on the immediate left and other on immediate right.

Here are some examples using Pascal’s triangle.

Example1. Expand ${\color{Red} (x+a)^{3}}$ using Pascal’s Triangle.

Solution: For n=3 , the numbers in 4th row of Pascal’s triangle are 1,3,3,1. Using them we get,

$\dpi{120} (x+a)^{3}= 1(x)^{3}a^{0}+3x^{2}a^{1}+3x^{1}a^{2}+1x^{0}a^{3}$

$\dpi{120} {\color{Red} 1}x^{3}+{\color{Red} 3}x^{2}a+{\color{Red} 3}xa^{2}+{\color{Red} 1}a^{3}$

Example2. Expand $\dpi{120} {\color{Red} (x-a)^{5}}$ using Pascal’s Triangle.

Solution: For n=5, the numbers in the 6^th row of Pascal’s Triangle are 1,5,10,10,5,1.

$\dpi{120} (x-a)^{5}=1x^{5}a^{0}-5x^{4}a^{1}+10x^{3}a^{2}-10x^{2}a^{3}+5x^{1}a^{4}-1x^{0}a^{5}$

$\dpi{120} ={\color{Red} 1}x^{5}-{\color{Red} 5}x^{4}a+{\color{Red} 10}x^{3}a^{2}-{\color{Red} 10}x^{2}a^{3}+{\color{Red} 5}xa^{4}-{\color{Red} 1}a^{5}$

Important: Each term has combined power same as n, i.e sum of powers in each term is same as n.

Exponent of first term in binomial expansion start with n and keep on decreasing till it reaches to 0 in last term, same way exponents of second term start with 0 and keep on increasing till it reach to n in last term.

General formula for Binomial Theorem

$\dpi{150} \mathbf{(x+a)^{n}= \sum_{r=0}^{n}\binom{n}{r}x^{n-r}a^{r}}$

Some important conclusions from the Binomial Theorem:

Total number of terms in binomial expansion is n+1.
The coefficients of terms equidistant from the beginning and end are equal. These coefficients are known as binomial coefficients.
The terms in the expansion of $\dpi{120} \mathbf{(x-a)^{n}}$ are alternatively positive and negative first being positive always.
The coefficient of $\dpi{120} \mathbf{x^{r}}$ in (r+1)th term in the expansion of $\dpi{120} \mathbf{(x+a)^{n}}$ is $\dpi{120} \mathbf{\binom{n}{r}}$ .

Pascal’s Triangle is not easy to use as it is not easy to memorize or draw Pascal’s triangle every time for large value of n so here combination formula comes handy. This is also called binomial coefficient formula and is represented as $\dpi{120} \mathbf{\binom{n}{r}}$ .

Combination formula:

$\dpi{150} \mathbf{\binom{n}{r}={^n}C_r=\frac{n!}{r!(n-r)!}}$

Example: $\dpi{120} \mathbf{\binom{7}{3}={^7}C_3=\frac{7!}{3!(7-3)!}} =35$

Formula for rth term in binomial expansion:

$\dpi{150} \mathbf{T_{r+1}=\binom{n}{r}x^{n-r}a^{r}}$

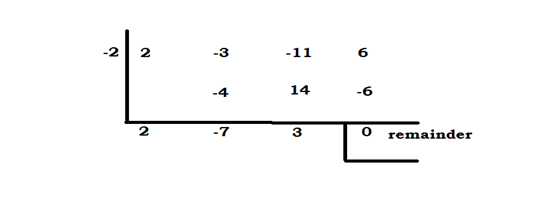
Example3. Find 13^th term in the expansion of $\dpi{120} {\color{Red} \left ( 9x-\frac{1}{3\sqrt{x}} \right )^{18}}$

Solution: $\dpi{120} T_{13}= T_{12+1}=\binom{18}{12}9x^{18-12}\left ( \frac{-1}{3\sqrt{x}} \right )^{12}$

$\dpi{120} =\frac{18!}{12!6!}(9x)^{6}\frac{1}{3^{12}\left ( \sqrt{x} \right )^{12}}$

$\dpi{120} =\left (18564 \right ) 9^{6}x^{6}\frac{1}{3^{12}x^{6}}$

= 18564

Example4. Find a, if 17^th and 18^th terms in the expansion of $\dpi{120} {\color{Red} (2+a)^{50}}$ are equal.

Solution: Using formula for rth term in binomial expansion,

$\dpi{120} T_{17}= T_{16+1}=\binom{50}{16}2^{50-16}a^{16}$

$\dpi{120} =\frac{50!}{16!34!}2^{34}a^{16}$

$\dpi{120} T_{18}= T_{17+1}=\binom{50}{17}2^{50-17}a^{17}$

$\dpi{120} =\frac{50!}{17!33!}2^{33}a^{17}$

Given that, $\dpi{120} \mathbf{T_{17}=T_{18}}$

$\dpi{120} \frac{50!}{16!34!}2^{34}a^{16}=\frac{50!}{17!33!}2^{33}a^{17}$

$\dpi{120} \frac{2^{34}}{16!34!}a^{16}=\frac{2^{33}}{17!33!}a^{17}$ ( cancelled 50! from both sides)

$\dpi{120} \frac{2^{34}}{16!34!}*\frac{17!33!}{2^{33}}=\frac{a^{17}}{a^{16}}$

$\dpi{120} \frac{2*17}{34}=a$

1 =a

Example5. Find 4^th term from the end in the expansion of $\dpi{120} {\color{Red} \left ( \frac{3}{x^{2}}-\frac{x^{3}}{6} \right )^{7}}$

Solution: Clearly, the given expansion contain 8 terms.

So, 4^th term from end = (8-4+1) =5^th term from the beginning.

So, required term

$\dpi{120} T_{5}= T_{4+1}=\binom{7}{4}\left ( \frac{3}{x^{2}} \right )^{7-4}\left ( \frac{-x^{3}}{6} \right )^{4}$

$\dpi{120} =\frac{7!}{4!3!}\left ( \frac{3}{x^{2}} \right )^{3}\left ( \frac{-x^{3}}{6} \right )^{4}$

$\dpi{120} =35 \frac{3^{3}}{\left ( x^{2} \right )^{3}}*\frac{\left ( -x^{3} \right )^{4}}{6^{4}}$

$\dpi{120} =35\frac{27x^{12}}{1296x^{6}}=\frac{35x^{6}}{48}$

Example6. Find the middle term in the expansion of $\dpi{120} {\color{Red} \left ( \frac{x}{3}+9y \right )^{10}}$

Solution: Here n=10 which is an even number. So $\dpi{120} \left ( \frac{10}{2} +1\right )th$ = 6^th term is the middle term. Hence middle term is,

$\dpi{120} T_{6}= T_{5+1}=\binom{10}{5}\left ( \frac{x}{3} \right )^{10-5}\left ( 9y \right )^{5}$

$\dpi{120} =\frac{10!}{5!5!}\frac{x^{5}}{3^{5}}9^{5}y^{5}$

$\dpi{120} =252\frac{x^{5}}{3^{5}}9^{5}y^{5}$

$\dpi{120} =252* 3^{5}x^{5}y^{5}= 61236 x^{5}y^{5}$

Note: When n is odd then there are two middle terms given as,

$\dpi{120} \left ( \frac{n+1}{2} \right )th$ and $\dpi{120} \left ( \frac{n+1}{2} +1\right )th$

For example when n is 7 then there are two middle terms

$\dpi{120} \left ( \frac{7+1}{2} \right )th = 4th$ and $\dpi{120} \left ( \frac{7+1}{2} +1\right )th =5th$

Example7. Find the term independent of x in the expansion of $\dpi{120} {\color{Red} \left ( 3x^{2}-\frac{1}{2x^{3}}\right )^{10}}$

Solution: Let (r+1)th term is independent of x in the given expression.

$\dpi{120} T_{r+1}=\binom{10}{r}\left ( 3x^{2} \right )^{10-r} \left (\frac{-1}{2x^{3}} \right ) ^{r}$

$\dpi{120} = \binom{10}{r}3^{10-r}\left (x^{2} \right )^{10-r}\left ( \frac{-1}{2} \right )^{r}\left ( \frac{1}{x^{3}} \right )^{r}$

$\dpi{120} =\binom{10}{r}3^{10-r}\left ( \frac{-1}{2} \right )^{r}x^{20-2r}\left ( x^{-3} \right )^{r}$

$\dpi{120} =\binom{10}{r}3^{10-r}\left ( \frac{-1}{2} \right )^{r}x^{20-5r}$

This term will be independent of x if ,

20-5r = 0

r = 4

Therefore,(4+1)=5^th term is independent of x.

Practice problems:

Find 7^th term in the expansion of $\dpi{120} \left ( 3x^{2}-\frac{1}{x^{3}} \right )^{10}$
If the coefficients of (2r+4)th and (r-2)th terms in the expansion of $\dpi{120} \left ( 1+x \right )^{18}$ are equal, then find r.
Find the term independent of x in the following expression. $\dpi{120} \left ( 2x+\frac{1}{3x^{2}} \right )^{9}$
Find the middle term in the expansion of $\dpi{120} \left ( x-\frac{1}{x} \right )^{10}$

Answers:

1) $\dpi{120} \frac{17010}{x^{10}}$

2) r = 6

3) 1792/9

4) -252

End Behavior of a Polynomial

August 21, 2019/by admin_ct

How to determine end behavior of a Polynomial function

End behavior describes the behavior of the function towards the ends of x axis when x approaches to –infinity or + infinity.

The two important factors determining the end behavior are its degree and leading coefficient.

Degree: it is the highest exponent of variable present in the polynomial .

Leading coefficient: It is the constant attached with leading term(term having highest exponent).

Here is a summary of all the possible cases.

Degree	Leading coefficient	End behavior	Graph examples.
Even	Positive	Both ends up Y–>∞ as X–>-∞ Y–>∞ as X–>∞	$\mathbf{Y=x^{2}}$
Even	Negative	Both ends down Y–>-∞ as X–>-∞ Y–>-∞ as X–>∞	$\mathbf{Y=-x^{2}}$
Odd	Positive	Falls to left and rise to right Y–>-∞ as X–>-∞ Y–>∞ as X–>∞	$\mathbf{Y=x^{3}}$
Odd	Negative	Falls to left and rise to right Y–>∞ as X–>-∞ Y–>-∞ as X–>∞	$\mathbf{Y=-x^{3}}$

Example1: Find end behavior of the given polynomial function.

${\color{Red} P(x)= 3x^{5}+x^{4}-5x^{2}+2x-1}$

Solution: Degree = 5(odd)

Leading coefficient = Positive

This is third case from the table given above so its left end will fall and right end will rise.

Y–>- ∞ as X–>-∞

Y–>∞ as X–>∞

Example2: Find end behavior of given polynomial function.

${\color{Red} P(x)= -x^{4}+4x^{2}}$

Solution: Degree = 4(even)

Leading coefficient = Negative

This is second case from the table given above so its both ends will fall down.

Y–>-∞ as X–>-∞

Y–>-∞ as X–>∞

Practice problems:

Determine end behavior of the following polynomial functions.

$P(x)=-x^{3}+2x^{2}-5x$
$P(x)=x^{6}-4x^{4}$

Answer:

Y–>∞ as X–>- ∞, Y–>-∞ as X–>∞
Y–> ∞ as X–>-∞ , Y–>∞ as X–>∞

Graphing Polynomials

August 21, 2019/by admin_ct

How to graph Polynomials

To graph any polynomial function, we need to know the real roots(zeroes) along with their multiplicity and end behavior of the polynomial. As we are already aware about end behavior of polynomials in previous section, we will talk about roots and their multiplicity. How multiplicity affect the graph of polynomial.

While sketching the graphs of polynomial functions we should keep in mind that graph of polynomials is always smooth without any holes, breaks or sharp corners.

Multiplicity of zeroes: This refers to the number of times a factor associated with that zero repeat itself in the polynomial expression. In simple words it is the exponent of the associated factor.

Some facts:

If x=a is a zero of the polynomial p(x) with multiplicity k $p(x)=(x-a)^{k}$ then,

If k is odd then graph will cross the x-axis at x=a.
If k is even then graph only touch the x-axis and not actually cross it. It bounce back in same direction.
If then the graph will flatten out at x=a .
A polynomial with degree n will have at most n-1 turning points(humps) in the graph.

It is easy to sketch the polynomial when given in factored form. If not given in factored form then we have to find its zeroes using rational root theorem and factoring which is another topic to be discussed separately.

Steps used in graphing Polynomials:

Predict the end behavior of given polynomial using degree and leading coefficient .
Find zeroes of given polynomial and rewrite it in factored form if not given already in factored form.
Find y intercept by substituting x as 0 in the given function.
Plot the x intercepts(zeroes) and y intercept using rules of multiplicity given above.
Connect all the points keeping in mind the end behavior.

Example1: Graph the polynomial function

${\color{Red} p(x)=x^{3}-x^{2}-2x}$

Solution:

Step 1) degree = 3(odd)

Leading coefficient= Positive

This graph will fall towards left and rise to right.

Step 2)

$p(x)=x\left ( x^{2}-x-2 \right )$

=x(x-2)(x+1)

Zeros are x=-1 ,0, 2

Step 3) Plug in x=0 to find y intercept.

P(0) = 0-0-2(0)= 0

Y intercept : (0,0)

Step 4 ) Plotting all the points we get following graph.

Example2: Graph the polynomial function

${\color{Red} p(x)=x(x+1)^{2}(x-1)^{3}}$

Solution:

Step 1) Degree= 1+2+3= 6 (even)

leading coefficient = positive

Both ends will rise up.

Step 2) Already in factored form.

X=-1 ,multiplicity 2(touch x axis at -1and bounce back)

X=0 , multiplicity 1 (intersect at x=0)

X=1 ,multiplicity 3 (cross x axis but get flat at x=1)

Step 3) Plug in x=0 to find y intercept.

P(0)= 0(1)(-1) = 0 => (0,0)

Step 4) Plotting all the x intercepts(zeroes) and y intercept and connecting them we get the following graph.

Practice problems:

Sketch the following polynomial functions.

$p(x)=x^{4}-x^{3}-6x^{2}$
$p(x)=-x^{5}+4x^{3}$
p(x)=-x(x+2)(x-2)(x+3)
$p(x)= (x-1)(x+2)^{2}$

Solving Polynomial inequalities

August 21, 2019/by admin_ct

How to solve Polynomial Inequalities

A polynomial function f(x) which takes of any of these forms f(x)>0 , f(x) ≥0 , f(x)<0, f(x)≤0 is called polynomial inequality.

To solve polynomial inequalities , following procedure is used.

Find polynomial function in factored form if not given already in factored form. Then find its zeros.
Find intervals using these zeros on a number line.
Check each interval by substituting any point from that interval into the factored form of polynomial function.
Make a sign chart which will help you to decide the domain for final answer.

Example1: Determine the x values that cause the polynomial function to be (a) zero, (b) positive, and (c) negative.

f(x)=(x+2)(x+1)(x-5)

Solution:

Step 1) As the given polynomial function already in factored form so we just need to find the zeros.

(x+2)(x+1)(x-5) = 0

x+2 =0 , x+1 =0 , x-5 =0

Zeros are : x = -2,-1,5

Step 2) Using these zeros on a number line, we get the number line divided into following intervals.

(- ∞,-2) , (-2,-1), (-1,5) ,(5,∞)

Step 3) Next we check these intervals by substituting any point from each interval into factored form of polynomial function. Remember not to use end points of these intervals and we are concerned only with signs not the exact values.

For interval (-∞,-2) , lets substitute x= -3

f(-3) = (-3+2)(-3+1)(-3-5)

= (-)(-)(-) < 0 (Negative)

For interval (-2,-1), lets substitute x = -1.5

f(-1.5) = (-1.5+2)((-1.5+1)(-1.5-5)

= (+)(-)(-) > 0 (positive)

For interval (-1,5) , lets substitute x=0

f(0) = (0+2)(0+1)(0-5)

= (+)(+)(-) < 0 (Negative)

For interval (5, ) , lets assume x=6

f(6) = (6+2)(6+1)(6-5)

= (+)(+)(+) > 0 (Positive)

Now we can write answer for each part .

Zeros x= -2,-1,5
Positive (-2,-1) U (5,∞ )
Negative (-∞ ,-2) U (-1,5)

This process was explained in detailed steps given above. Once we understand the process ,we don’t need to show all this work and all this work can be squeezed into a sign chart.

Intervals	(x+2)(x+1)(x-5)	Result
(-∞,-2)	(-)(-)(-)	(-)	< 0
(-2,-1)	(+)(-)(-)	(+)	> 0
(-1,5)	(+)(+)(-)	(-)	< 0
(5,∞ )	(+)(+)(+)	(+)	> 0

Example2. Complete the factoring if needed, and solve the polynomial inequality using a sign chart.

${\color{Red} 2x^{3}-3x^{2}-11x+6\geq 0}$

Solution:

step1) First we assume all possible rational zeros using Rational root theorem.

±1, ±2, ±3, ±6, ±1/2, ±3/2

Step2 ) We can check these zeros one by one using synthetic division. After checking several zeros we got that-2 gives 0 remainder. So we got first zero as x=-2 .

Step 3) using the terms in the bottom line we get the quotient polynomial as $2x^{2}-7x+3$ which can be factored further to get remaining two zeros. Since this is quadratic polynomial so we can try factoring .

$2x^{2}-7x+3$

$2x^{2}-6x-x+3$

2x(x-3)-1(x-3)

(x-3)(2x-1)

Using zero product rule, we get the zeros as

x-3=0 , 2x-1 =0

x = 3 , x = 1/2

We get the complete factored form as:

(x+2)(x-3)(2x-1) ≥ 0

Step 4) Now we use these three zeros to find intervals on number line.

(-∞, -2) , (-2, 1/2 ), (1/2 ,3) ,(3, ∞ )

Step 5) Next we check each interval by substituting any point from each interval into factored form of original equation and make a sign chart. For answer we accept only those intervals which have positive results because this polynomial inequality has ≥ sign.

Intervals	(x+2)(x-3)(2x-1)	Result
(-∞ ,-2)	(-)(-)(-)	(-)	Not accepted
(-2, 1/2 )	(+)(-)(-)	(+)	Accepted
(1/2 ,3)	(+)(-)(+)	(-)	Not accepted
(3, ∞ )	(+)(+)(+)	(+)	Accepted

Step 6) The intervals having positive results are accepted and forms the final answer but we need to use closed intervals because of sign.

So answer is : [-2, ½ ] U [3,∞ )

Example3. Solve the following inequalities for the given polynomial functions.

a) f(x)>0 b) f(x)≥ 0 c) f(x)<0 d) f(x) ≤ 0

1) ${\color{Red} f(x)=\left ( x^{2}+4 \right )\left ( 2x^{2}+3 \right )}$

Solution: Using zero product rule, we get its solution as non real numbers. Also when we look at this function, we see that both factors have positive terms ( $x^{2}$ is always a positive term).

This means this function will always be positive for all real values of x. So the answer for part a and part b will be all real numbers which is represented in interval forms as (-∞,∞ )

This function will never be negative. So answers for different parts can be written as,

(-∞,∞ )
(-∞,∞ )
No solution
No solution

2) ${\color{Red} f(x)=\left ( x^{2}+1 \right )\left ( -2-3x^{2} \right )}$

Rewriting this function in simplified form by taking out negative sign,

$f(x)=-\left ( x^{2}+1 \right )\left ( 2+3x^{2} \right )$

Here both factors have positive terms so both factors are positive but negative sign outside, make the result negative. That means this function will always remain negative for all real values of x (-∞,∞ ). So answers for different parts can be written as,

No solution
No solution
(-∞,∞ )
(-∞,∞ )

Example 4. Consider the collection of all rectangles that have lengths 2 in. less than twice their widths. Find the possible widths (in inches) of these rectangles if their perimeters are less than 200 in.

Solution:

Lets assume width of rectangle = x

Then length of rectangle = 2x-2

Given that , Perimeter < 200

2( length+ width) < 200

2( 2x-2 +x ) < 200

3x -2 < 100

3x < 102

x < 34

As length and width always positive integers(>0) so,

x > 0 and 2x-2 >0

2x >2 => x > 1

So the possible widths of rectangles are given as,

1 < x < 34 (inches)

Practice problems:

1) Determine the x values that cause the polynomial function to be (a) zero, (b) positive, and (c) negative.

$f(x)=(x+7)(x+4)(x-6)^{2}$

2) Complete the factoring if needed, and solve the polynomial inequality using a sign chart.

$2x^{3}-5x^{2}-x+6 \geq 0$

3) Solve the following inequalities for the given polynomial functions.

a) f(x)>0 b) f(x)≥ 0 c) f(x)<0 d) f(x)≤ 0

$f(x)=\left (2x^{2}-2x+5 \right )\left ( 3x-4 \right )^{2}$

4)The Grovenor Candy Co. finds that the cost of making a certain candy bar is $0.13 per bar. Fixed costs amount to $2000 per week. If each bar sells for $0.35, find the minimum number of candy bars that will earn the company a profit.

Answers:

1) a. x=-7,-4,6 b. (-∞ ,-7)U(-4,6)U(6,∞ ) c) (-7,-4)

2) (-1, 3/2 ) U (2,∞ )

3) a.(-∞, 4/3 )U(4/3 ,∞ ) b. (-∞,∞ ) c) No solution d) x=4/3

4) Minimum 9091 candies

Solving Rational equations in one variable

August 20, 2019/by admin_ct

How to solve Rational equations in one variable

Equations involving rational expressions or fractions of the form $\frac{f(x)}{g(x)}$ , are called rational equations. To solve rational equations we use the following procedure:

Step 1) First find least common denominator (LCD) of all the terms of the equation. LCD may contain variables .

Step2) Get rid of fractions by multiplying both sides of the equation with LCD. Simplify the equation.

Step 3) Resulting simplified algebraic equation may have solutions that are not the solutions of original equation. These are extraneous solutions. For this reason we must check each solution by substituting in original equation.

Example1. Solve the equation algebraically. Support your answer numerically .

${\color{Red} x+5=\frac{14}{x}}$

Solution: step1)

Here only rational expression is $\frac{14}{x}$ . So LCD = x.

Step 2) To get rid of this fractional term we multiply both sides with x.

x(x+5) = 14

$x^{2}+5x-14=0$ Subtract 14 from both sides.

(x+7)(x-2) = 0 Get the factors

(x+7) =0 or (x-2) =0 Zero factor property

x = -7 , x =2

Step 3) Confirm Numerically,

For x =-7, $-7+5 = \frac{14}{-7}$

-2 = -2 It is working !

For x= 2, 2+5 = 14/2

7 = 7 This too is working !

So the solutions are x=-7 ,2

Example2. Solve the equation algebraically. Support your answer numerically and identify any extraneous solutions.

${\color{Red} x + \frac{4x}{x-3}=\frac{12}{x-3}}$

Solution: step 1) LCD = (x-3)

Step2) Multiply all the terms with (x-3) and we get,

x(x-3) + 4x = 12

x(x-3) +4x-12 = 0

x(x-3) +4(x-3) = 0

(x-3)(x+4) = 0

(x-3)=0 or (x+4) = 0

x= -4, 3

step 3) Confirm numerically,

For x= -4 , Plugin into original equation.

$-4+\frac{4(-4)}{-4-3}=\frac{12}{-4-3}$

$-4 +\frac{16}{7}=-\frac{12}{7}$

$-\frac{12}{7}=-\frac{12}{7}$ This is working !

For x= 3,

$3+\frac{4(3)}{3-3}=\frac{12}{3-3}$

$3+\frac{12}{0}=\frac{12}{0}$ which is not defined, so not working.

Extraneous solution is x=3.

Only solution is x= -4 .

Example3. Solve the equation algebraically. Support your answer numerically and identify any extraneous solutions.

${\color{Red} \frac{3}{x+2}+\frac{6}{x^{2}+2x}=\frac{3-x}{x}}$

Solution: Step 1) Write the denominators in factored form wherever possible and then find LCD.

$\frac{3}{x+2}+\frac{6}{x(x+2)}=\frac{3-x}{x}$

LCD = x(x+2)

Step2 ) Multiply all the terms with LCD to get rid of fractions.

3(x)+6 = (3-x)(x+2)

$3x+6=3x+6-x^{2}-2x$

$x^{2}+2x=0$

x(x+2) = 0

x = -2,0

Step 3) Confirm numerically,

For x=-2, Plugin into original equation

$\frac{3}{-2+2}+\frac{6}{(-2)^{2}+2(-2)}=\frac{3-(-2)}{-2}$

$\frac{3}{0}+\frac{6}{0}= -\frac{5}{2}$ Which is not defined.

So x=-2 not working.

For x= 0 ,

$\frac{3}{0+2}+\frac{6}{(0)^{2}+2(0)}=\frac{3-(0)}{0}$

$\frac{3}{2}+\frac{6}{0}=\frac{3}{0}$ which is again not defined.

So x=0 also not working. Hence both solutions are extraneous solutions.

So this rational equation doesn’t have any solutions.

Example 4. Solve the equation algebraically. Support your answer numerically and identify any extraneous solutions.

${\color{Red} \frac{4x}{x+4}+\frac{5}{x-1}=\frac{15}{x^{2}+3x-4}}$

Solution: step 1) Write the denominators in factored form wherever possible and then find LCD.

$\frac{4x}{x+4}+\frac{5}{x-1}=\frac{15}{(x+4)(x-1)}$

LCD = (x+4)(x-1)

Step 2) Multiply all the terms with LCD to get rid of fractions.

4x(x-1) + 5(x+4) = 15

$4x^{2}-4x+5x+20-15=0$

$4x^{2}+x+5=0$

This quadratic equation is not factorable. So we can use quadratic formula to get the solutions for x.

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a} = \frac{-1\pm \sqrt{1^{2}-4(4)(5)}}{2(4)}$

$x=\frac{-1\pm \sqrt{-79}}{8}$ which are not real solutions.

So no real solutions possible for this rational equation.

Example 5. Mid Town Sports Apparel, Inc., has found that it needs to sell golf hats for $2.75 each in order to be competitive. It costs $2.12 to produce each hat, and it has weekly overhead costs of $3000.

(a) Let x be the number of hats produced each week. Express the average cost (including overhead costs) of producing one hat as a function of x.

(b) Solve algebraically to find the number of golf hats that must be sold each week to make a profit. Support your answer graphically.

(c) How many golf hats must be sold to make a profit of $1000 in 1 week? Explain your answer.

Solution:

Part a) Cost of producing one hat =$2.12

Cost of producing x hats = 2.12x

Total cost function C(x) = variable cost+ fixed cost

C(x) = 2.12x +3000

Average cost function $\frac{C(x)}{x}= \frac{2.12x+3000}{x}$

Part b) To make a profit we need to find break even point , when cost function is equal to revenue function.

Sale price of each hat = $2.75

Revenue function R(x) = 2.75x

C(x) = R(x)

2.12x +3000 = 2.75x

3000 = 0.63x

4761.90 = x

x ≈ 4762

4762 hats must be sold each week to make a profit.

Part c) Revenue – cost = profit

2.75x–(2.12x+3000) = 1000

0.63x -3000 = 1000

x = 4000/0.63 = 6349.206

x ≈ 6350

6350 hats must be sold each week to earn a profit of $1000.

Practice problems:

Solve the following equations algebraically. Support your answer numerically and identify any extraneous solutions.

$\frac{x-3}{x}-\frac{3}{x+1}+\frac{3}{x^{2}+x}=0$
$2-\frac{1}{x+1}=\frac{1}{x^{2}+x}$
$x^{2}+\frac{5}{x}=8$

4) Consider all rectangles with an area of 182 sq.ft . Let x be the length of one side of such a rectangle.

(a) Express the perimeter P as a function of x.

(b) Find the dimensions of the rectangle that has the least

perimeter. What is the least perimeter ?

Answers:

X=0,5 ; extraneous solution x=0
X=-1 , ½ ; extraneous solution x=-1
x≈-3.1 , x≈0.661, x≈2.439
a) P(x) = 2x+(364/x) b) x ≈13.49 , p=53.96

Solving Rational Inequalities

August 20, 2019/by admin_ct

How to solve rational inequalities

The inequalities having rational expressions or fractions either on one side or on both sides are called rational inequalities. This is similar to solving rational expression in one variable but solving rational inequalities also consists of making intervals and sign chart after finding zeros.

Here is the procedure to solve rational inequalities.

Step 1) Move all the terms to left side, making right side as 0.

Step2) Then find least common denominator (LCD) of all the terms of the equation. LCD may contain variables .

Step3) Simplify the terms on top after making same denominators.

Step4) Find the zeros and the x values where function is undefined. To get these values we set numerator and denominator = 0 and solve.

Step5) Using these x values, find intervals on number line.

Step6) Then check these intervals and make a sign chart. Depending on the inequality sign we choose the intervals for final answer. Open and closed intervals are also chosen according to the given inequality sign.

Lets work on some examples to understand the process.

Example1: Solve the following inequality.

$\dpi{120} {\color{Red} \frac{2x+4}{x-1}\geq 5}$

Solution: Step1) Move all the terms to left to get right side as 0

$\dpi{120} \frac{2x+4}{x-1}- 5\geq 0$

Step2) Here LCD=(x-1) lets make all denominators same using LCD.

$\dpi{120} \frac{2x+4}{x-1}- \frac{5}{1}\frac{\left (x-1 \right )}{\left (x-1 \right )}\geq 0$

Step3) Simplify the terms on top.

$\dpi{120} \frac{2x+4-5(x-1)}{x-1}\geq 0$

$\dpi{120} \frac{-3x+9}{x-1}\geq 0$

Step4) Setting numerator and denominator =0 and solving , we get x = 1,3

X=3 is the zero of the function and at x=1 this function is undefined so we consider both these values to get intervals.

Step 5) Intervals are (-∞,1) ,(1,3), (3,∞) . Then we check each interval by testing any point from each interval into simplified rational expression in step 3.

Step 6) lets get a sign chart.

Intervals	$\dpi{120} \frac{-3x+9}{x-1}$	result
(-∞, 1)	$\dpi{120} \frac{\left ( + \right )}{\left ( - \right )}$	–	Not accepted
(1,3)	$\dpi{120} \frac{\left ( + \right )}{\left ( + \right )}$	+	Accepted
(3, ∞)	$\dpi{120} \frac{\left ( - \right )}{\left ( + \right )}$	–	Not accepted

Since this inequality has ≥ sign so we choose that closed interval which gives positive result.

But x=1 make this function undefined so 1 can’t be included in the solution interval. Therefore final answer is (1,3]

Example2. Solve the following inequality using a sign chart.

$\dpi{120} {\color{Red} \frac{x^{3}(x-2)}{(x+3)^{2}}< 0}$

Solution: Here we have the rational expression already factored and simplified. So we don’t need to work for initial three steps and can directly jump to step 4. For that we set numerator and denominator =0 and get x values as x=-3,0 and x=2.

Using these x values, we get intervals as, (-∞,-3) ,(-3,0) ,(0,2) and (2,∞). Now we get a sign chart.

Intervals	$\dpi{120} \frac{x^{3}(x-2)}{(x+3)^{2}}$	result
(-∞,-3)	$\dpi{120} \frac{(-)(-)}{(+)}$	+	Not accepted
(-3,0)	$\dpi{120} \frac{(-)(-)}{(+)}$	+	Not accepted
(0,2)	$\dpi{120} \frac{(+)(-)}{(+)}$	–	Accepted
(2, ∞)	$\dpi{120} \frac{(+)(+)}{(+)}$	+	Not accepted

Since this inequality has < sign so we accept those open intervals which gives negative results.

Therefore final answer is (0,2).

Rational inequalities involving absolute value.

We have to be careful while solving rational inequalities with absolute sign, sometimes we need to use definition of absolute function to get perfect sign chart. We consider both positive and negative cases while simplifying rational inequality with absolute sign. Follow the given examples to understand the concept.

Example 3. Solve the following rational inequality using sign chart.

$\dpi{120} {\color{Red} \frac{(x-3)}{\left | x+2 \right |}< 0}$

Solution: Setting numerator =0 we get the zero as x=3 and x=-2 make this function undefined. Using these two points we get the intervals on number line as (-∞, -2) ,(-2,3) and (3, ∞). Lets get a sign chart.

Intervals	$\dpi{120} \frac{(x-3)}{\left \| x+2 \right \|}$	Result
(-∞,-2)	$\dpi{120} \frac{(-)}{(+)}$	–	Accepted
(-2,3)	$\dpi{120} \frac{(-)}{(+)}$	–	Accepted
(3,∞)	$\dpi{120} \frac{(+)}{(+)}$	+	Not accepted

Since this inequality has < sign so we choose those open intervals which gives negative result.

Therefore final answer is (-∞, -2)U(-2,3).

Example4. Solve the following rational inequality.

$\dpi{120} {\color{Red} \frac{\left | x-1 \right |}{x+2}< 1}$

Solution: Step 1) First we subtract 1 from both sides to get right side as 0.

$\dpi{120} \frac{\left |x-1 \right |}{x+2}- 1< 0$

Step2) LCD = (x+2) lets make all denominators same .

$\dpi{120} \frac{\left |x-1 \right |}{(x+2)}- 1\frac{\left (x+2 \right )}{\left (x+2 \right )}< 0$

Step 3) Simplify the terms on top

$\dpi{120} \frac{\left | x-1 \right |-(x+2)}{x+2}< 0$

We have to simplify the top having absolute value, so two cases arise using definition of absolute functions.

$\dpi{120} \left | x-1 \right |=\begin{cases} -(x-1) & \text{ if } x< 1\\ (x-1) & \text{ if } x\geq 1 \end{cases}$

Case 1. When x-1 ≥ 0 => x ≥ 1 Then we have |x-1|= (x-1)

$\dpi{120} \frac{(x-1)-(x+2)}{x+2}< 0$

$\dpi{120} \frac{-3}{x+2}< 0$

x+2 > 0

x > -2

But domain is x≥ 1 so solution set would be [1,∞)

Case 2. When x-1 < 0 => x < 1 then we have |x-1|=-(x-1)

$\dpi{120} \frac{-(x-1)-(x+2)}{x+2}< 0$

$\dpi{120} \frac{-(2x+1)}{x+2}< 0$

Multiply both sides with -1 and inequality sign get reversed.

$\dpi{120} \frac{(2x+1)}{x+2}> 0$

Now set numerator and denominator =0 to get x values for intervals. We get x = -1/2 and x= -2 so the intervals are :

(-∞,-2) , (-2, -1/2) ,(-1/2 ,∞)

Intervals	$\dpi{120} \frac{2x+1}{x+2}$	result
(-∞, -1/2)	$\dpi{120} \frac{(-)}{(-)}$	+	Accepted
(-2, -1/2)	$\dpi{120} \frac{(-)}{(+)}$	–	Not accepted
( -1/2 , ∞ )	$\dpi{120} \frac{(+)}{(+)}$	+	Accepted

As this inequality has > sign so we accept those open intervals which gives positive results. But in this case domain is x<1 so the answer is (-∞,-2)U( -1/2 ,1 ) .

For final answer we have to combine the results of case 1 and case 2 both. Combining them we get final answer as,

(-∞,-2)U( -1/2, ∞ )

Solving an inequality involving a Radical.

Example5. Solve the following inequality.

$\dpi{120} {\color{Red} (2x-1)\sqrt{x+4}< 0}$

Solution: We know that radicals are not defined for negative values so,

x+4 ≥ 0 => x ≥ -4

We have to consider this domain while solving this inequality.

Zeros of this function are x= ½ and x=-4

So we get the intervals as (-4,½) , (½ ,∞)

As this inequality has < sign so we accept those open intervals which gives negative result.

So the final answer is (-4, ½)

Practice problems:

1) Determine the real values of x that cause the function to be

(a) zero, (b) undefined, (c) positive, and (d) negative.

$\dpi{120} \frac{\sqrt{x+5}}{(2x+1)(x-1)}$

Solve the following inequalities using sign chart wherever possible.

2) $\dpi{120} \frac{1}{(x+1)}+\frac{1}{(x-3)}\leq 0$

3) $\dpi{120} \frac{(x-5)\left | x-2 \right |}{2x-3}\geq 0$

4) $\dpi{120} (x-3)\sqrt{x+1}\geq 0$

Answers:

x=-5 b. x=-½, 1 and x < -5 c. (-5, -1/2) U(1,∞) d) (-1/2,1)
(-∞,-1) U [1,3)
[5,∞)
{-1} U [3,∞)

Logistic Functions and their graphs

August 19, 2019/by admin_ct

Logistic functions use exponential function. This function, though related to exponential function , can’t be obtained from by translations, reflections ,horizontal and vertical stretches or shrinks. So we give logistic function a formal introduction.

Let a, b, c and k be positive constants with 0<b<1. A logistic growth function in x is a function that can be written in the form,

$\dpi{150} \mathbf{f(x)= \frac{c}{1+ab^{x}}}$ or $\dpi{150} \mathbf{f(x)= \frac{c}{1+ae^{-kx}}}$

where constant C is limit to growth and is also called carrying capacity.

If b>1 or k<1 then these formulas yield logistic decay functions.

Unless otherwise stated , all logistic functions are taken as logistic growth functions.

If we set a=c=k=1 then we obtain basic logistic function as,

$\dpi{150} \mathbf{f(x)= \frac{1}{1+e^{-x}}}$

All logistic functions have graphs like basic logistic function as shown below.

Following are the properties of logistic function graph:

Horizontal lines y=0 and y=c are the horizontal asymptotes.
Y intercept is $\dpi{120} (0,\frac{c}{1+a})$
Domain of logistic function is all real numbers (-∞,∞ ) and range is (0,c) i.e 0<y<c
Graph is increasing from left to right.
Central point $\dpi{120} \left ( \frac{lna}{k},\frac{c}{2} \right )$ is the point of maximum growth. This is also called point of symmetry. To the left of this point, growth rate is increasing and towards right of this point, growth rate is decreasing.

Example1: Graph the following logistic function. Identify the asymptotes, y-intercept, and point of maximum growth.

${\color{Red} f(x)= \frac{5}{1+e^{-10x}}}$

Solution: Comparing the given function with $\dpi{120} f(x)= \frac{c}{1+ae^{-kx}}$

We get a=1,k=10 and c=5

Horizontal asymptote: y=0 and y=5

Y intercept :

$\dpi{120} \left (0,\frac{c}{1+a} \right )=(0,\frac{5}{1+1})= (0, 2.5)$

Point of maximum growth:

$\dpi{120} \left ( \frac{lna}{k},\frac{c}{2} \right )=\left ( \frac{ln1}{10},\frac{5}{2} \right )= (0,2.5)$

End behavior :

$\dpi{120} \lim_{x->-\infty }f(x) = 0$

$\dpi{120} \lim_{x->\infty }f(x) = 5$

Using the above information we can draw the graph manually.

Example2: The number of students infected with flu at Springfield High School after t days is modeled by the function

$\dpi{120} {\color{Red} f(x)= \frac{800}{1+49e^{-0.2t}}}$

(a) What was the initial number of infected students?

(b) When will the number of infected students be 200?

(c) The school will close when 300 of the 800-student body are infected. When will the school close?

Solution: To find initial number of infected students at the end of first day , we plugin t=0.

$\dpi{120} f(0)= \frac{800}{1+49e^{-0.2*0}}$

$\dpi{120} f(0)= \frac{800}{1+49(1)}= \frac{800}{50} = 16$

So 16 students were infected initially.

b) We are given f(t) = 200 and we need to find t (number of days).

$\dpi{120} 200= \frac{800}{1+49e^{-0.2t}}$

$\dpi{120} 1+49e^{-0.2t}=\frac{800}{200}=4$

$\dpi{120} 49e^{-0.2t}= 4-1 =3$

$\dpi{120} e^{-0.2t}=\frac{3}{49}$

$\dpi{120} -0.2t = ln\left ( \frac{3}{49} \right )$

$\dpi{120} t = \frac{-1}{0.2}ln\left ( \frac{3}{49} \right )$

t = 13.996 ≈ 14 days

$\dpi{120} 300= \frac{800}{1+49e^{-0.2t}}$

$\dpi{120} 1+49e^{-0.2t}=\frac{800}{300}=\frac{8}{3}$
$\dpi{120} 49e^{-0.2t}= 4-1 =3$

$\dpi{120} e^{-0.2t}=\frac{3}{49}$

$\dpi{120} -0.2t = ln\left ( \frac{3}{49} \right )$

$\dpi{120} t = \frac{-1}{0.2}ln\left ( \frac{3}{49} \right )$

t = 16.904 17 days

School will close after 17 days.

Practice problems:

Graph the following logistic function. Identify the asymptotes, y-intercept, and point of maximum growth.

$\dpi{120} f(x)= \frac{6}{1+0.8e^{-2x}}$

2. Solve the following logistic equation

$\dpi{120} \frac{8}{1+3e^{-x}}=5$

3. Using 20th-century U.S. census data, the population of Ohio can be modeled by

$\dpi{120} p(t)=\frac{12.79}{1+2.402e^{-0.0309t}}$

where P is the population in millions and t is the number of years since April 1, 1900. Based on this model, when was the population of Ohio 10 million?

Answers:

Asymptotes y=0, y=6, Y intercept =(0, 3.3) ,Point of max growth (-0.1, 3)
X=1.609
Year 1970

Log Functions and their Inverse

August 17, 2019/by admin_ct

For any positive numbers b and x where b ≠ 1, log function is defined as $\dpi{120} \log_{b}x$ and is read as “log base b of x”

Logarithmic and exponential functions are related with the following expression.

$\dpi{120} \mathbf{\log_{b}x=y}$ if and only if $\dpi{120} \mathbf{b^{y}=x}$

Using above relation log functions can be written as exponential functions and vice versa.

Example: Rewrite the following log expressions into equivalent exponential expressions.

$\dpi{120} \log_{2}32=5 \Rightarrow 2^{5}=32$
$\dpi{120} \log_{5}125=x \Rightarrow 5^{x}=125$
$\dpi{120} 2\log_{2}512=x \Rightarrow 2^{\frac{x}{2}}=512$
$\dpi{120} \log_{b}1=0 \Rightarrow b^{0}=1$
$\dpi{120} \log_{b}b=1 \Rightarrow b^{1}=b$

There are two types of log functions. One with base 10 is called common logarithm and other with base e is called natural logarithm.

Common logarithm Natural logarithm

$\dpi{120} \mathbf{\log_{10}x}$ = log(x) $\dpi{120} \mathbf{\log_{e}x}$ = ln(x)

Inverse of log functions:

Finding inverse of log function is very easy and similar to solving an equation and converting log function into an exponential equation. To find inverse of log functions, we use following algorithm.

Replace the function notation f(x) by y.
Switch over x and y.
Isolate the log function on one side.
Convert log equation into equivalent exponential equation using rule $\dpi{120} \mathbf{\log_{b}x=y}\mathbf{\Rightarrow b^{y}=x}$
Solve the exponential equation for y and at last replace y with $\dpi{120} \mathbf{f^{-1}(x)}$ .

Lets work on some examples to understand this process.

Example1.Find inverse of log equation

$\dpi{120} {\color{Red} f(x)=\log_{3}(x-2)}$

Solution: step1) replace f(x) with y.

$\dpi{120} y=\log_{3}(x-2)$

Step 2) switch over x and y.

$\dpi{120} x=\log_{3}(y-2)$

Step 3) log function is already isolated.

Step 4) convert log equation into exponential equation.

$\dpi{120} 3^{x}=y-2$

Step 5) Solve for y.

$\dpi{120} 3^{x}+2=y$

Replace y with $\dpi{120} \mathbf{f^{-1}(x)}$

$\dpi{120} f^{-1}(x)=3^{x}+2$

Example2. Find inverse of the following log function.

$\dpi{120} {\color{Red} f(x)=3\log_{3}(x+3)+1}$

Solution: Using the same procedure as for above example we proceed as follows.

$\dpi{120} y =3\log_{3}(x+3)+1$

switch over x and y

$\dpi{120} x =3\log_{3}(y+3)+1$

start isolating y

$\dpi{120} \frac{x-1}{3} =\log_{3}(y+3)$

$\dpi{120} 3^{\left ( \frac{x-1}{3} \right )}=y+3$

$\dpi{120} 3^{\left ( \frac{x-1}{3} \right )}-3=y$

$\dpi{120} 3^{\left ( \frac{x-1}{3} \right )}-3= f^{-1}(x)$

Example3: Find inverse of the following natural log function.

f(x) = -ln(1 – 2x) + 1

Solution: Let y = -ln(1 – 2x) + 1

Switch over x and y ,

x = -ln(1 – 2y) + 1

x-1 = -ln(1 – 2y)

Multiply both sides by -1,

1-x = ln(1-2y)

$\dpi{120} e^{1-x}=1-2y$ natural log (ln) has base ‘e’

$\dpi{120} 2y= 1-e^{1-x}$

$\dpi{120} y= \frac{1}{2}\left (1-e^{1-x} \right )$

Example4. Find the inverse of following exponential function.

$\dpi{120} {\color{Red} f(x)= 2*3^{3x}-1}$

Solution:

let $\dpi{120} y=2*3^{3x}-1$

After switching over x and y we get,

$\dpi{120} x=2*3^{3y}-1$

$\dpi{120} x+1=2*3^{3y}$

$\dpi{120} \frac{x+1}{2}= 3^{3y}$

$\dpi{120} \log_{3}\left ( \frac{x+1}{2} \right )= 3y$

$\dpi{120} \frac{1}{3}\log_{3}\left ( \frac{x+1}{2} \right )= y$

$\dpi{120} \frac{1}{3}\log_{3}\left ( \frac{x+1}{2} \right )= f^{-1}(x)$

Example 5. Find inverse of following exponential function.

$\dpi{120} {\color{Red} f(x)= 1-2e^{-2x}}$

Solution:

let $\dpi{120} y = 1-2e^{-2x}$

Switching over x and y we get,

$\dpi{120} x = 1-2e^{-2y}$

$\dpi{120} 2e^{-2y}= 1-x$

$\dpi{120} e^{-2y}= \frac{1-x}{2}$

$\dpi{120} -2y=ln\left ( \frac{1-x}{2} \right )$

$\dpi{120} y= -\frac{1}{2}ln\left ( \frac{1-x}{2} \right )$

$\dpi{120} f^{-1}(x)= -\frac{1}{2}ln\left ( \frac{1-x}{2} \right )$

Practice problems:

Find the inverse of following log functions.

$\dpi{120} f(x)= \log_{2}(x-3)-5$
$\dpi{120} f(x)= -2\log_{2}(x-1)+2$

Find the inverse of following exponential functions.

$\dpi{120} f(x)= 2^{x}-3$
$\dpi{120} f(x)= -5e^{-x}+2$

Answers:

1. $\dpi{120} f^{-1}(x)= 2^{(x+5)}+3$

2. $\dpi{120} f^{-1}(x)= \frac{1}{2}10^{\left ( \frac{2-x}{2} \right )}+1$

1. $\dpi{120} f^{-1}(x)= \log_{2}(x+3)$

2. $\dpi{120} f^{-1}(x)= -ln\left ( \frac{2-x}{5} \right )$

Solving Logarithmic equations

August 16, 2019/by admin_ct

How to solve logarithmic equations

The equations having logs are called logarithmic equations. Before going to solve logarithmic equations, we should be familiar with basic logarithmic rules. Here is a recap.

$\dpi{120} \mathbf{\log_{b}A- \log_{b}B=\log_{b}\left ( \frac{A}{B} \right )}$ Quotient formula

$\dpi{120} \mathbf{\log_{b}A+ \log_{b}B=\log_{b}\left ( AB \right )}$ Product formula

$\dpi{120} \mathbf{A\log_{b}C = \log_{b}C^{A}}$ Power formula

$\dpi{120} \mathbf{\log_{b}A= \frac{logA}{logb}}$ Change of base formula

All the above formulas are applicable for natural logs(ln) too.

Some facts:

$\dpi{120} \log_{b}b =1$

$\dpi{120} \log_{b}1 =0$

$\dpi{120} \log_{b}x =\log_{b}y \Rightarrow x=y$

$\dpi{120} \log_{10}10 =1$

$\dpi{120} \log_{10}100 =2$

$\dpi{120} \log_{10}1000 =3$ and so on…

There are two types of logarithmic equations. One having logs on both sides with same base. These are easy to solve as log with same base on both sides get eliminated and inside expressions get equated. Equations with different bases become more complex.

Lets work on some first kind of logarithmic equations.

Example1 Solve $\dpi{120} {\color{Red} \log_{2}(x-1)=\log_{2}4}$

Solution: As we can see, this equation has log with same base(2) on both sides so we can just equate the inner expressions.

x-1 = 4 => x = 5

Example 2 Solve $\dpi{120} {\color{Red} \log_{10}(x+1)+\log_{10}(x-1)=\log_{10}8}$

Solution: Here first we simplify the expression on left side , make it a single log expression using product formula.

$\dpi{120} \log_{10}(x+1)+\log_{10}(x-1)=\log_{10}8$

$\dpi{120} \log_{10}\left [ (x+1)(x-1) \right ]=\log_{10}8$

(x+1)(x-1) = 8

$\dpi{120} x^{2}-1=8$

$\dpi{120} x^{2}=9$

x=-3 , 3

Note: Don’t forget to check the solutions by plug in them back into original equation.

Check: When we plug in x=-3 we get

$\dpi{120} \log_{10}(x+1)=\log_{10}(-3+1)=\log_{10}(-2)$

and we know that inside of a log function can’t be negative as logs are not defined for negative values.

So only solution is x=3

Log written without base is assumed as log with base 10 and is called common logarithm. Here is an example to show this.

Example 3. Solve for x , log(-x+1)=log(x+5)

Solution: This type of logs are called common logs and we can continue to solve them like this without writing any base as long as there are only logs(without base) on both sides.

log(-x+1)=log(x+5)

-x+1 = x+5

1-5 = x+x

-4 = 2x

-2 = x

When we plugin back x=-2 into original equation it gives valid log functions so x= -2 is a solution.

It is okay to have x values as negative and 0 but we can’t accept such values as solution which gives inside of logs as negative because

Log( negative values) = undefined

Log(0) = undefined

Solving equations having natural logs:

Natural logs(ln) is nothing but same as log with base e instead of 10. We can use same formulas as we used for logs .

Example4 . solve ln(x+1)-ln(x-4) = ln3

Solution: using quotient rule on left side,

$\dpi{120} ln\left ( \frac{x+1}{x-4} \right )=ln3$

ln from both sides can be dropped and we can equate the inner parts.

$\dpi{120} \frac{x+1}{x-4}=3$

X+1 = 3(x-4)

X+1 = 3x-12

1+12 =3x-x

13 = 2x => x = 13/2

After checking by plugging it into original equation we get that x= 13/2 is a valid solution!

Example 5. Solve the logarithmic equation and find the valid solution.

$\dpi{120} {\color{Red} \log_{3}(x+2)-\log_{3}x=\log_{3}(2x-1)-\log_{3}(3x-12)}$

Solution: using quotient rule on both sides,

$\dpi{120} \log_{3}\left ( \frac{x+2}{x} \right )=\log_{3}\left ( \frac{2x-1}{3x-12} \right )$

Logs with same bases can be dropped from both sides.

$\dpi{120} \frac{x+2}{x}=\frac{2x-1}{3x-12}$

Now this is simple algebraic equation which can be solved further by cross multiplying both sides.

(x+2)(3x-12) = x(2x-1)

$\dpi{120} 3x^{2}-6x-24=2x^{2}-x$

$\dpi{120} x^{2}-5x-24=0$

(x-8)(x+3) = 0 [factored the quadratic equation]

X= -3, 8

Check: when we plug in back x=-3 and x=8 into original equation , we get that only x=8 is a valid solution as x=-3 results into log of negative number which is undefined.

When all terms of logarithmic equation doesn’t have logs and any one term is a constant term. This is second type of logarithmic equation unlike the first type where we had all log terms on both sides. To solve these kind of problems we use formula,

If $\dpi{120} \mathbf{y=\log_{b}x}$ then $\dpi{120} \mathbf{x=b^{y}}$

Example 6. Solve for x, $\dpi{120} {\color{Red} \log_{2}(x+2)= 5}$

Solution: using the formula given above rewrite the logarithmic equation as an exponential equation.

$\dpi{120} (x+2)= 2^{5}$

x+2 = 32 => x=30

For equations having natural logs(ln) instead of common logs, we use base e as shown in the example below.

Example7. Solve the given logarithmic equation for x. Round your answer to nearest hundredth.

ln(2x-1) = 5

Solution: Since natural log has base e so ln get changed to base e on other side.

$\dpi{120} (2x-1)=e^{5}$

2x-1 = 148.4131

2x = 149.4131

X = 74.7065 ≈ 74.71

Example8 . Solve log(x) +log(x+15) = 2

Solution: Using product rule on left side,

log[x(x+15)] = 2

log(x^2 +15x) = 2

We know that common log get changed to base 10 so,

$\dpi{120} x^{2}+15x = 10^{2}$

$\dpi{120} x^{2}+15x- 100=0$

Now get factors of this quadratic equation.

(x+20)(x-5) = 0

x=-20 , x=5

Check: when we plug in x=-20 into original equation we get log(-20) which is not defined. So x=-20 is not a valid solution.

Only solution is x=5 !

Example9. Solve $\dpi{120} {\color{Red} \log_{2}x-\log_{2}(\sqrt{x}-1)=2}$

Solution: Using quotient rule on left side,

$\dpi{120} \log_{2}\left ( \frac{x}{\sqrt{x}-1} \right )=2$

Changing log to exponential form,

$\dpi{120} \frac{x}{\sqrt{x}-1}= 2^{2}$

x = 4(√x-1 )

x = 4√x – 4

x+4 = 4√x

Squaring both sides,

$\dpi{120} (x+4)^{2}=\left ( 4\sqrt{x} \right )^{2}$

$\dpi{120} x^{2}+8x+16=16x$

$\dpi{120} x^{2}-8x+16=0$

(x-4)(x-4) = 0

x= 4

Practice problems:

Solve the following logarithmic equations. Round your answers to nearest hundredth wherever possible.

$\dpi{120} \log_{10}(x)+\log_{10}(x-6)=\log_{10}2x-7$
$\dpi{120} 2 \log_{3}(x+1)=\log_{3}(x+2)-\log_{3}(x-3)$
ln(6x-5) = 3
$\dpi{120} \log_{6}x+\log_{6}(x-9)=2$
$\dpi{120} \log_{5}(x-3)=\log_{5}\left ( \sqrt{x+3} \right )$

Answers:

X=7
No solution
X=4.18
X=12
X=6

Simplify logarithmic expressions

August 14, 2019/by admin_ct

How to simplify Logarithmic expressions

The expressions having logs or natural logs(ln) are called logarithmic expressions. Before going to simplify logarithmic expressions , we should be familiar with basic logarithmic rules. Here is a recap.

$\dpi{120} \mathbf{\log_{b}A- \log_{b}B=\log_{b}\left ( \frac{A}{B} \right )}$ Quotient formula

$\dpi{120} \mathbf{\log_{b}A+ \log_{b}B=\log_{b}\left ( AB \right )}$ Product formula

$\dpi{120} \mathbf{A\log_{b}C = \log_{b}C^{A}}$ Power formula

$\dpi{120} \mathbf{\log_{b}A= \frac{logA}{logb}}$ Change of base formula

All the above formulas are applicable for natural logs(ln) too.

Some facts:

$\dpi{120} \log_{b}b =1$

$\dpi{120} \log_{b}1 =0$

$\dpi{120} \log_{b}x =\log_{b}y \Rightarrow x=y$

$\dpi{120} \log_{10}10 =1$

$\dpi{120} \log_{10}100 =2$

$\dpi{120} \log_{10}1000 =3$ and so on…

Lets start with solving simple logarithmic expressions.

Solving Logarithmic expressions without calculator

Example1. Solve the expression using properties of logs.

$\dpi{120} {\color{Red} \log_{3}81} = \log_{3}3^{4}$ write 81 using exponents

$\dpi{120} =4\log_{3}3$ Using power formula

= 4(1) = 4

$\dpi{120} {\color{Red} \log_{5}0.04} = \log_{5}\left ( \frac{4}{100} \right )$ get rid of decimals

$\dpi{120} = \log_{5}\left ( \frac{1}{25} \right )$ reduced the fraction to lowest terms

$\dpi{120} =\log_{5}5^{-2}$ write using exponents

$\dpi{120} = -2\log_{5}5$ used power formula

= -2 (1) => -2 using fact that $\dpi{120} \log_{b}b=1$

$\dpi{120} {\color{Red} \log_{\frac{1}{2}}(8)} = \frac{log8}{log\frac{1}{2} }$ using change of base formula

$\dpi{120} = \frac{log2^{3}}{\left ( log1-log2 \right )}$ using quotient formula

$\dpi{120} =\frac{3log2}{0-log2}$ using fact that log1 =0

$\dpi{120} =\frac{3log2}{-log2} =\frac{3}{-1} = -3$

$\dpi{120} {\color{Red} \log_{9}3}= \frac{log3}{log9}$ using change of base formula

$\dpi{120} =\frac{log3}{log3^{2}}$

$\dpi{120} =\frac{log3}{2log3} = \frac{1}{2}$

Evaluating Logarithmic expressions

Example2. Use $\dpi{120} {\color{Red} \log_{5}3\approx 0.683 and \log_{5}7\approx 1.209}$ to approximate the following

Solution:

$\dpi{120} {\color{Red} \log_{5}\left (\frac{3}{7} \right )}= \log_{5}3- \log_{5}7$ using quotient formula

= 0.683 – 1.209

= -0.526

$\dpi{120} {\color{Red} \log_{5}(63)}= \log_{5}\left ( 3^{2}*7 \right )$

$\dpi{120} =\log_{5}3^{2}+ \log_{5}7$ using product formula

$\dpi{120} =2\log_{5}3+ \log_{5}7$ using power formula

=2(0.683) + 1.209

= 1.366 + 1.209 = 2.575

$\dpi{120} {\color{Red} \log_{5}\left (\frac{9}{49} \right )}= \log_{5}9- \log_{5}49$ using quotient formula

$\dpi{120} =\log_{5}3^{2}- \log_{5}7^{2}$

$\dpi{120} =2\log_{5}3-2 \log_{5}7$ using power formula

= 2(0.683) -2(1.209)

= 1.366 – 2.418 = -1.052

Expanding logarithmic expressions

Example 3. Expand the following expressions using properties of logs.

$\dpi{120} {\color{Red} \log_{2}\left ( \frac{4y^{3}}{x^{2}} \right )} = \log_{2}\left ( 4y^{3} \right )-\log_{2}\left ( x^{2} \right )$ using quotient formula

$\dpi{120} =\log_{2}4+\log_{2}y^{3}-\log_{2}x^{2}$ using product formula

$\dpi{120} =2\log_{2}2+3\log_{2}y-2\log_{2}x$ using power formula

$\dpi{120} =2+3\log_{2}y-2\log_{2}x$ using the fact $\dpi{120} \log_{2}2=1$

$\dpi{120} {\color{Red} \log_{6}\left ( \frac{36x^{3}}{\sqrt{y}} \right )} = \log_{6}\left ( 36x^{3} \right )-\log_{6}\left ( \sqrt{y} \right )$ using quotient formula

$\dpi{120} = \log_{6}\left ( 6^{2} \right )+\log_{6}x^{3}-\log_{6}y^{\frac{1}{2}}$ using product formula

$\dpi{120} = 2\log_{6} 6+3\log_{6}x-\frac{1}{2}\log_{6}y$ using power formula

$\dpi{120} = 2(1)+3\log_{6}x-\frac{1}{2}\log_{6}y$ using the fact $\dpi{120} \log_{6}6=1$

$\dpi{120} = 2+3\log_{6}x-\frac{1}{2}\log_{6}y$

$\dpi{120} {\color{Red} \log_{2}\left ( \frac{32\sqrt[3]{x}}{y^{3}} \right )} = \log_{2}\left ( 32\sqrt[3]{x} \right )-\log_{2}\left ( y^{3} \right )$ using quotient formula

$\dpi{120} = \log_{2}\left ( 32\right )+\log_{2}\sqrt[3]{x}-\log_{2}y^{3}$ product formula

$\dpi{120} = \log_{2}\left ( 2^{5}\right )+\log_{2}x^{\frac{1}{3}}-\log_{2}y^{3}$

$\dpi{120} = 5\log_{2}2+ \frac{1}{3}\log_{2}x-3\log_{2}y$ power formula

$\dpi{120} = 5+ \frac{1}{3}\log_{2}x-3\log_{2}y$

Condensing Logarithmic expressions

To condense the log expressions, we apply reverse of power formula , product formula and quotient formula.

Example 4. Condense the following expressions into single logarithm using properties of logs.

1) $\dpi{120} {\color{Red} 7\log_{4}2+5\log_{4}x+3\log_{4}y}$

$\dpi{120} \log_{4}2^{7}+\log_{4}x^{5}+\log_{4}y^{3}$ reverse power formula

$\dpi{120} \log_{4}\left ( 2^{7}x^{5}y^{3} \right )$ reverse product formula

$\dpi{120} \log_{4}\left ( 128x^{5}y^{3} \right )$

2) $\dpi{120} {\color{Red} 4\log_{3}2+2\log_{3}3-2\log_{3}6}$

$\dpi{120} \log_{3}2^{4}+\log_{3}3^{2}-\log_{3}6^{2}$ reverse power formula

$\dpi{120} \log_{3}\left ( 2^{4}3^{2} \right )-\log_{3}6^{2}$ reverse product formula

$\dpi{120} \log_{3}\left ( \frac{2^{4}3^{2}}{6^{2}} \right )$ reverse quotient formula

$\dpi{120} \log_{3}\left ( \frac{144}{36} \right )=\log_{3}4$

3) ln(3x)-4ln(y)- (1/2) ln(z)

$\dpi{120} ln(3x)- ln y^{4}-lnz^{\frac{1}{2}}$ reverse power formula

$\dpi{120} ln(3x)- \left [ln y^{4}+lnz^{\frac{1}{2}} \right ]$ negative sign factored out

$\dpi{120} ln(3x)-ln\left ( y^{4}z^{\frac{1}{2}} \right )$ reverse product formula

$\dpi{120} ln\left ( \frac{3x}{y^{4}\sqrt{z}} \right )$ reverse quotient formula

Practice problems:

Solve the expression using properties of logs.

$\dpi{120} \log_{\frac{1}{3}}(27)$

$\dpi{120} \log_{4}(0.25)$

Use log2 ≈ 0.3010 and log3 ≈ 0.4771 to approximate the following.

log(12)

Log(5)

Expand the following expressions using properties of logs.

$\dpi{120} \log_{3}\left ( \frac{9yz^{3}}{x^{5}} \right )$

$\dpi{120} ln\left ( \frac{36\sqrt[4]{x}}{y^{2}z} \right )$

Condense the following expressions into single logarithm using properties of logs.

$\dpi{120} \frac{1}{4}\log_{5}81-\left ( 2\log_{5}6-\frac{1}{2}\log_{5}4 \right )$

$\dpi{120} \frac{1}{2}\log_{4}x +\frac{1}{2}\log_{4}y$

Answers:

-3 , -1
0791 , 0.699
$\dpi{120} 2+\log_{3}y+3\log_{3}z-5\log_{3}x$ , $\dpi{120} 2+\frac{1}{4}\log_{6}x-2\log_{6}y-\log_{6}z$
$\dpi{120} \log_{5}\left ( \frac{1}{6} \right )$ , $\dpi{120} \log_{4}\left ( \sqrt{xy} \right )$

Archives

How to determine end behavior of a Polynomial function

How to graph Polynomials

How to solve Polynomial Inequalities

How to solve Rational equations in one variable

How to solve rational inequalities

Rational inequalities involving absolute value.

Solving an inequality involving a Radical.

Inverse of log functions:

How to solve logarithmic equations

Solving equations having natural logs:

How to simplify Logarithmic expressions

Solving Logarithmic expressions without calculator

Evaluating Logarithmic expressions

Expanding logarithmic expressions

Condensing Logarithmic expressions